§ 19. Напряжённость электростатического поля. Принцип суперпозиции
Для изучения свойств электростатического поля удобно использовать такую его характеристику, которая не зависит от числового значения пробного заряда и позволяет определить силу, действующую на заряд со стороны поля в любой его точке. Для гравитационного поля такой характеристикой, не зависящей от массы тела, является ускорение свободного падения . Какая физическая величина является характеристикой электростатического поля?
Напряжённость электростатического поля. Пусть электростатическое поле создано в вакууме точечным зарядом Q > 0. Если в некоторую точку поля поместить пробный положительный заряд q0, на него будет действовать кулоновская сила отталкивания, модуль которой .
Сила не может служить характеристикой поля, так как её модуль пропорционален значению пробного заряда q0. Однако отношение модуля силы, которой электростатическое поле точечного заряда Q действует на пробный заряд q0, не зависит от значения пробного заряда:
(19.1)
и, следовательно, может служить характеристикой поля.
Эту характеристику называют напряжённостью электростатического поля и обозначают . Напряжённость характеризует силовое действие поля на вносимые в него заряды.
Напряжённость электростатического поля — физическая векторная величина, равная отношению силы, которой поле действует на пробный заряд, к значению этого заряда:
(19.2)
С учётом выражений (19.1) и (19.2) можно определить модуль напряжённости электростатического поля, созданного точечным зарядом Q, в точке, находящейся на расстоянии r от него:
Таким образом, модуль напряжённости поля, создаваемого в вакууме точечным зарядом, прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости.
Если заряд Q находится в однородной среде с диэлектрической проницаемостью ε, то модуль напряжённости поля .
Из выражения следует, что единицей напряжённости электростатического поля в СИ является ньютон на кулон
. В СИ широко используют другое название этой единицы — вольт на метр
.
Зная напряжённость электростатического поля, можно определить силу, действующую на любой точечный заряд в любой точке этого поля:
(19.3)
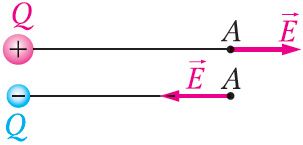
Напряжённость поля, как и сила, величина векторная. Направление напряжённости поля совпадает с направлением силы, действующей на положительный пробный электрический заряд. Напряжённость в любой точке электростатического поля точечного заряда направлена вдоль прямой, соединяющей эту точку и точечный заряд, создающий поле. Напряжённость поля, созданного точечным положительным зарядом Q > 0, направлена от заряда, а напряжённость поля, созданного точечным отрицательным зарядом Q < 0, — к заряду (рис. 104).
1. Как изменится модуль напряжённости в некоторой точке поля, созданного точечным зарядом Q, если: а) расстояние r от заряда до этой точки увеличить вдвое; б) заряд Q увеличить вдвое, а расстояние r от заряда до этой точки уменьшить вдвое?
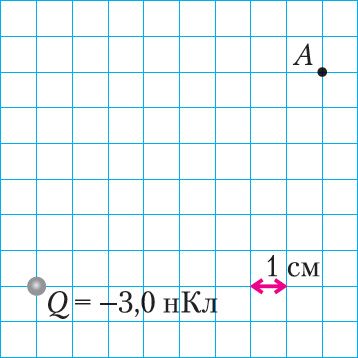
2. Как направлена в точке А напряжённость поля, созданного неподвижным точечным зарядом (рис. 105)? Чему равен модуль напряжённости поля в этой точке?
![]()
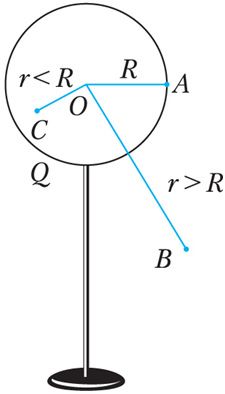
Модуль напряжённости поля уединённой проводящей сферы радиусом R, заряд которой Q (рис. 105.1), в точках на её поверхности r = R и вне сферы на расстоянии r > R от её центра определяют по формуле . В точках, находящихся внутри проводящей сферы r < R, напряжённость равна нулю
, если внутри этой сферы нет электрических зарядов.
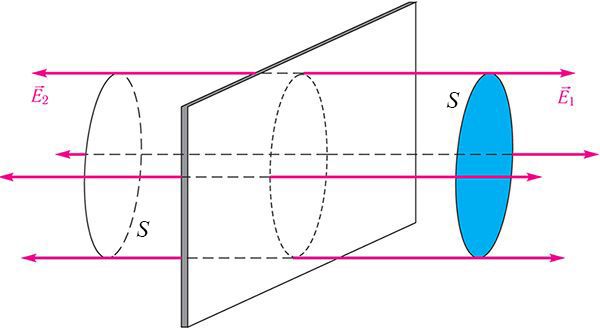
Напряжённость электростатического поля, создаваемого равномерно заряженной бесконечной плоскостью, одинакова во всех точках полупространства с каждой стороны от плоскости (при этом ), а её модуль
где S — площадь некоторого участка плоскости, — модуль заряда этого участка (рис. 105.2).
Интересно знать
Кроме гравитационного поля у Земли есть электрическое и магнитное поля. Модуль напряжённости электрического поля у поверхности Земли в среднем составляет . Электрическое поле Земли меняется во времени. Избыточный отрицательный электрический заряд земного шара колеблется около –6 · 105 Кл.