§ 19. Напряжённость электростатического поля. Принцип суперпозиции
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 19. Напряжённость электростатического поля. Принцип суперпозиции |
| Напечатано:: | Гость |
| Дата: | Пятница, 15 Август 2025, 12:22 |
Для изучения свойств электростатического поля удобно использовать такую его характеристику, которая не зависит от числового значения пробного заряда и позволяет определить силу, действующую на заряд со стороны поля в любой его точке. Для гравитационного поля такой характеристикой, не зависящей от массы тела, является ускорение свободного падения . Какая физическая величина является характеристикой электростатического поля?
Напряжённость электростатического поля. Пусть электростатическое поле создано в вакууме точечным зарядом Q > 0. Если в некоторую точку поля поместить пробный положительный заряд q0, на него будет действовать кулоновская сила отталкивания, модуль которой .
Сила не может служить характеристикой поля, так как её модуль пропорционален значению пробного заряда q0. Однако отношение модуля силы, которой электростатическое поле точечного заряда Q действует на пробный заряд q0, не зависит от значения пробного заряда:
(19.1)
и, следовательно, может служить характеристикой поля.
Эту характеристику называют напряжённостью электростатического поля и обозначают . Напряжённость характеризует силовое действие поля на вносимые в него заряды.
Напряжённость электростатического поля — физическая векторная величина, равная отношению силы, которой поле действует на пробный заряд, к значению этого заряда:
(19.2)
С учётом выражений (19.1) и (19.2) можно определить модуль напряжённости электростатического поля, созданного точечным зарядом Q, в точке, находящейся на расстоянии r от него:
Таким образом, модуль напряжённости поля, создаваемого в вакууме точечным зарядом, прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости.
Если заряд Q находится в однородной среде с диэлектрической проницаемостью ε, то модуль напряжённости поля .
Из выражения следует, что единицей напряжённости электростатического поля в СИ является ньютон на кулон
. В СИ широко используют другое название этой единицы — вольт на метр
.
Зная напряжённость электростатического поля, можно определить силу, действующую на любой точечный заряд в любой точке этого поля:
(19.3)
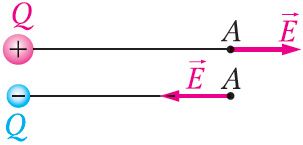
Напряжённость поля, как и сила, величина векторная. Направление напряжённости поля совпадает с направлением силы, действующей на положительный пробный электрический заряд. Напряжённость в любой точке электростатического поля точечного заряда направлена вдоль прямой, соединяющей эту точку и точечный заряд, создающий поле. Напряжённость поля, созданного точечным положительным зарядом Q > 0, направлена от заряда, а напряжённость поля, созданного точечным отрицательным зарядом Q < 0, — к заряду (рис. 104).
1. Как изменится модуль напряжённости в некоторой точке поля, созданного точечным зарядом Q, если: а) расстояние r от заряда до этой точки увеличить вдвое; б) заряд Q увеличить вдвое, а расстояние r от заряда до этой точки уменьшить вдвое?
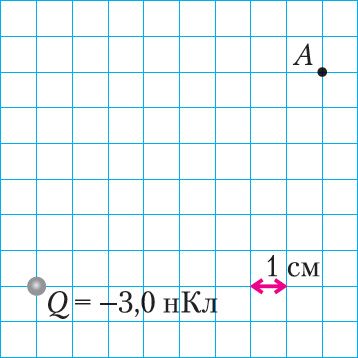
2. Как направлена в точке А напряжённость поля, созданного неподвижным точечным зарядом (рис. 105)? Чему равен модуль напряжённости поля в этой точке?
![]()
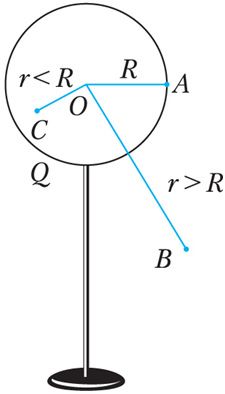
Модуль напряжённости поля уединённой проводящей сферы радиусом R, заряд которой Q (рис. 105.1), в точках на её поверхности r = R и вне сферы на расстоянии r > R от её центра определяют по формуле . В точках, находящихся внутри проводящей сферы r < R, напряжённость равна нулю
, если внутри этой сферы нет электрических зарядов.
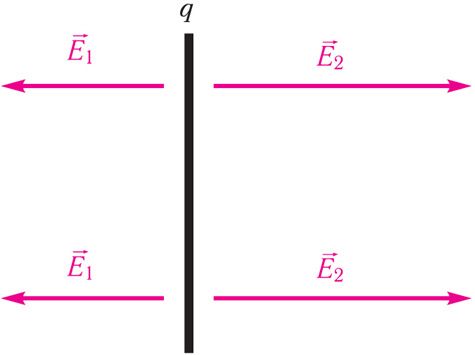
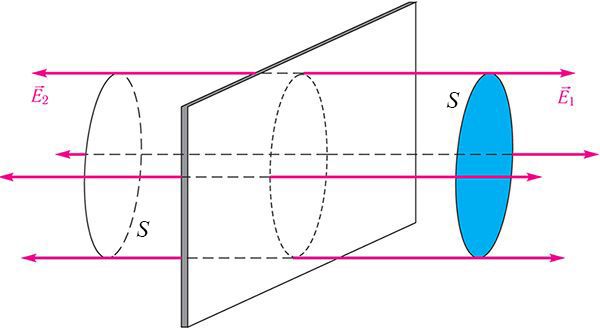
Напряжённость электростатического поля, создаваемого равномерно заряженной бесконечной плоскостью, одинакова во всех точках полупространства с каждой стороны от плоскости (при этом ), а её модуль
где S — площадь некоторого участка плоскости, — модуль заряда этого участка (рис. 105.2).
Интересно знать
Кроме гравитационного поля у Земли есть электрическое и магнитное поля. Модуль напряжённости электрического поля у поверхности Земли в среднем составляет . Электрическое поле Земли меняется во времени. Избыточный отрицательный электрический заряд земного шара колеблется около –6 · 105 Кл.
Принцип суперпозиции электрических полей. Пусть пробный заряд q0 находится в некоторой точке электростатического поля, созданного не одним, а несколькими точечными зарядами. Экспериментально установили, что результирующая сила, действующая на пробный заряд, равна векторной сумме сил, действующих со стороны электростатических полей этих точечных зарядов:
(19.4)
Воспользовавшись формулой (19.3), можно определить силы, действующие на пробный заряд:
,
,
,
, …,
,
где — результирующая напряжённость поля системы точечных зарядов, а
,
,
, ...,
— напряжённости полей в данной точке, создаваемых 1-м, 2-м, 3-м, …, n-м точечными зарядами.
Подставив эти выражения в соотношение (19.4), получим, что
если в данной точке пространства электростатическое поле создано системой точечных зарядов, то напряжённость результирующего поля в этой точке равна векторной сумме напряжённостей полей, создаваемых каждым из точечных зарядов системы в отдельности:
Это положение называют принципом суперпозиции полей.
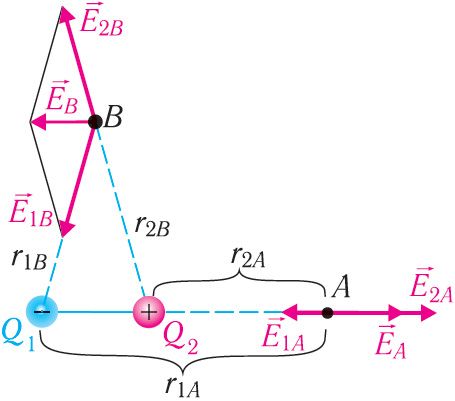
Воспользуемся принципом суперпозиции, чтобы определить в точках А и В напряжённости результирующего поля, созданного двумя точечными электрическими зарядами противоположных знаков Q1 < 0 и Q2 > 0, но с одинаковыми модулями (рис. 106).
![]()
Напряжённости и
полей, созданных зарядами Q1 и Q2, в точке А направлены вдоль прямой, соединяющей заряды, в противоположные стороны. Напряжённость
результирующего поля в точке А равна векторной сумме напряжённостей
и
и также направлена вдоль прямой, соединяющей заряды.
Напряжённость результирующего поля в точке В, находящейся вне прямой, соединяющей заряды, равна векторной сумме напряжённостей
и
. Определить её можно по правилу параллелограмма (см. рис. 106).
Принцип суперпозиции также применим и для определения напряжённости электростатического поля системы проводящих концентрических заряженных сфер.
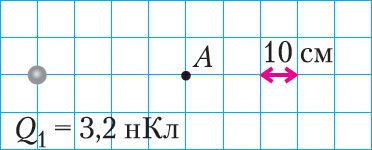
1. Чему равен модуль напряжённости поля, создаваемого точечным неподвижным зарядом Q1, в точке А (рис. 107)?
2. Где следует разместить ещё один такой же точечный заряд Q2 = Q1, чтобы в точке А модуль напряжённости результирующего поля оказался равным нулю?

![]()
1. Что называют напряжённостью электростатического поля?
2. Как рассчитать напряжённость электростатического поля точечного заряда в некоторой точке этого поля?
3. Как определить силу, действующую со стороны электростатического поля, на внесённый в него точечный заряд?
4. Можно ли назвать ускорение свободного падения напряжённостью гравитационного поля?
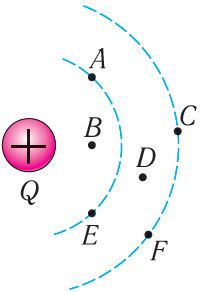
5. Пробный заряд помещают в разные точки электростатического поля, созданного зарядом Q (рис. 108). В каких точках модуль напряжённости поля максимален? минимален? В каких точках он одинаков?
6. Как направлена напряжённость поля, созданного точечным зарядом Q < 0; точечным зарядом Q > 0?
7. В чём заключается принцип суперпозиции электростатических полей?
![]()
8. Гравитационное поле Земли также можно характеризовать напряжённостью. Сравните выражения для электрической силы и силы тяжести
. Чему равна напряжённость гравитационного поля Земли вблизи её поверхности?
Пример 1. Два неподвижных точечных заряда Q1 = 6,70 нКл и Q2 = –13,3 нКл находятся в воздухе на расстоянии r = 5,00 см друг от друга. Определите модуль напряжённости электростатического поля в точке, находящейся на расстоянии r1 = 3,00 см от положительного заряда и r2 = 4,00 см от отрицательного.
Q1 = 6,70 нКл = 6,70 · 10–9 Кл
Q2 = –13,3 нКл = –1,33 · 10–8 Кл
r = 5,00 см = 5,00 · 10–2 м
r1 = 3,00 см = 3,00 · 10–2 м
r2 = 4,00 см = 4,00 · 10–2 м
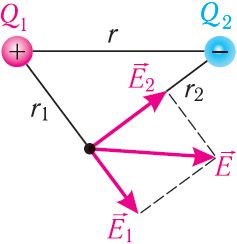
Решение: Согласно принципу суперпозиции, напряжённость результирующего поля (рис. 109) определяют по правилу параллелограмма. Здесь
и
— напряжённости полей, создаваемых точечными зарядами Q1 и Q2 в данной точке. Из условия задачи и теоремы Пифагора следует, что угол между
и
прямой.
Модуль напряжённости Е результирующего поля найдём по теореме Пифагора: . Так как заряды Q1 и Q2 точечные, то
,
.
С учётом этого
Ответ: .
![]()
Пример 2. Первоначально неподвижный шарик массой m = 10 г и зарядом q = 1,0 мкКл начинает падать с ускорением, модуль которого а = 8,0 . Шарик находится в электростатическом поле, напряжённость которого направлена вертикально вверх и одинакова во всех его точках. Определите напряжённость этого поля.
m = 10 г = 1,0 · 10–2 кг
q = 1,0 мкКл = 1,0 · 10–6 Кл
а = 8,0

Решение: В начальный момент на шарик действуют сила тяжести со стороны гравитационного поля Земли и электрическая сила
со стороны электростатического поля. Модуль ускорения, с которым начинает падать положительно заряженный шарик, меньше модуля ускорения свободного падения
. Следовательно, электрическая сила
электростатического поля направлена вертикально вверх и совпадает по направлению с напряжённостью. Модуль напряжённости определим, используя второй закон Ньютона:
. В проекции на вертикальную ось Оу (рис. 109.1) это уравнение имеет вид:
. Тогда
.
Ответ: напряжённость электростатического поля направлена вертикально вверх и её модуль .
Упражнение 14
1. В некоторую точку электростатического поля, в которой модуль напряжённости , помещают точечный заряд q = 4,00 нКл. Определите модуль силы, действующей на этот заряд со стороны электростатического поля.
2. Определите модуль точечного заряда, находящегося в воздухе, если на расстоянии r = 1,0 см от заряда модуль напряжённости поля
3. Два положительных точечных заряда находятся на расстоянии r0 = 10 см друг от друга. В точке, расположенной на прямой, соединяющей заряды, на расстоянии r1 = 8,0 см от первого заряда модуль напряжённости результирующего электростатического поля равен нулю. Определите отношение зарядов .
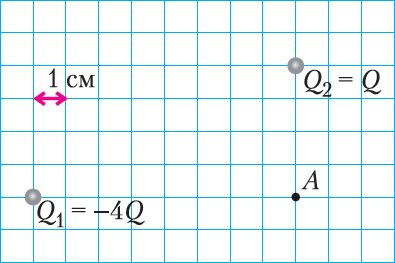
4. Электростатическое поле в точке создано неподвижными точечными зарядами Q1 = –4Q и Q2 = Q (рис. 110).
а) Изобразите в выбранном вами масштабе напряжённости и
полей, созданных каждым зарядом в точке А.
б) Обозначьте на рисунке направление результирующей напряжённости .
в) Определите модуль результирующей напряжённости EA поля, если |Q| = 8,0 нКл.
5. Пылинка массой m = 2,5 · 10–8 г имеет заряд q = 5,0 · 10–12 Кл. Напряжённость поля в точке, где находится пылинка, направлена вертикально вверх. Определите модуль напряжённости электростатического поля, если пылинка находится в равновесии.
![]()
6. Три одинаковых отрицательных точечных заряда, модули которых , расположены в вершинах равнобедренного прямоугольного треугольника. Определите напряжённость электростатического поля в точке пространства, находящейся на середине гипотенузы, длина которой а = 8,0 см.
7. Частица массой m = 2,0 мг и зарядом q = 9,5 пКл начинает двигаться в вакууме в электростатическом поле, модуль напряжённости которого . Напряжённость поля одинакова во всех его точках и направлена горизонтально. Определите модуль ускорения этой частицы и путь, пройденный ею за первую секунду движения.
8. Заряд находящейся в воздухе уединённой металлической сферы Q = 0,20 мкКл. Определите максимальное значение напряжённости электростатического поля, создаваемого зарядом этой сферы, если её диаметр d = 0,80 м.
9. Бесконечную равномерно заряженную плоскую пластину поместили в однородное электрическое поле, напряжённость которого перпендикулярна её поверхности. Модули результирующих напряжённостей полей слева и справа от пластины и
соответственно (рис. 110.1). Определите модуль силы, действующей на единицу площади S = 1,0 м2 пластины.