§ 7. Моделирование случайных событий. Метод Монте-Карло
7.3. Метод Монте-Карло
|
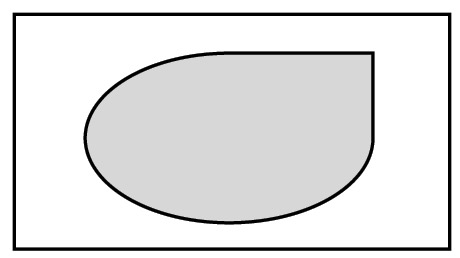
Метод Монте-Карло — это численный метод решения математических задач, который основан на использовании генератора случайных чисел. Генератор случайных чисел в методе Монте-Карло используется для моделирования случайных опытов (бросание монеты, игрального кубика, точки на плоскую фигуру) и случайных потоков (потоки писем, посылок, посетителей). Рассмотрим суть метода Монте-Карло на примере задачи определения площади некоторой плоской фигуры. Это приложение метода называют геометрическим методом Монте-Карло (пример 7.6). Прямоугольник с известной площадью в геометрическом методе Монте-Карло будем называть базовым. Очевидно, что с увеличением общего числа песчинок точность результата должна возрастать. Точность результата также можно повысить, если сделать минимальными размеры базового прямоугольника. Геометрический метод Монте-Карло освобождает от необходимости на самом деле разбрасывать и подсчитывать песчинки. |
Название метода Монте-Карло, конечно, связано с названием курорта, который является одним из центров игорного бизнеса, во многом построенного на игре в рулетку. Рулетка позволяет проводить случайный опыт с выпадением случайного целого числа от 0 до 36.
Пример 7.6. Пусть имеется плоская фигура, которая находится внутри прямоугольника с известной площадью S0. Засыплем мысленно прямоугольник тончайшим слоем песка. Если посчитать общее число n песчинок и число k тех песчинок, которые попали на фигуру, то приближенно площадь фигуры можно считать по формуле |