§ 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током
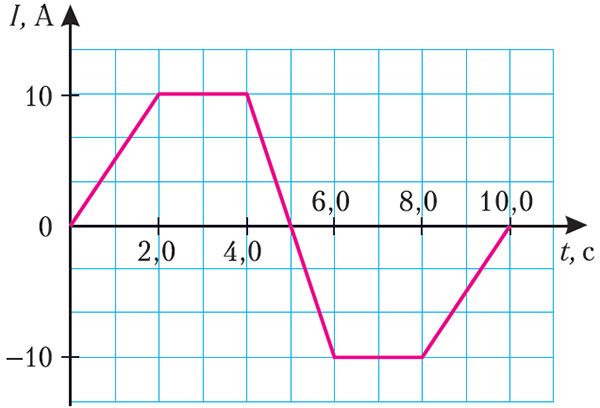
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.
L = 40 мГн = 4,0 · 10–2 Гн
Решение: ЭДС самоиндукции «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»=«/mo»«mo»-«/mo»«mi»L«/mi»«mfrac»«mrow»«mo»§#8710;«/mo»«mi»I«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«/math». Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:
1) от момента времени t1 = 0,0 с до момента времени t2 = 2,0 с сила тока изменяется на ΔI1 = 10 А за промежуток времени Δt1 = 2,0 с;
2) от момента времени t3 = 4,0 с до момента времени t4 = 6,0 с сила тока изменяется на ΔI2 = –20 А за промежуток времени Δt2 = 2,0 с;
3) от момента времени t5 = 8,0 с до момента времени t6 = 10,0 с сила тока изменяется на ΔI3 =10 А за промежуток времени Δt3 = 2,0 с.
Поскольку промежутки времени Δt1 = Δ t2 = Δ t3 = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt2 = 2,0 с (от t3 = 4,0 с до t4 = 6,0 с):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mfenced open=¨|¨ close=¨|¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«/mfenced»«mi»max«/mi»«/msub»«mo»=«/mo»«mi»L«/mi»«mfenced open=¨|¨ close=¨|¨»«mfrac»«mrow»«mo»§#8710;«/mo»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«/mrow»«mrow»«mo»§#8710;«/mo»«msub»«mi»t«/mi»«mn»2«/mn»«/msub»«/mrow»«/mfrac»«/mfenced»«mo».«/mo»«/math»
Таким образом,
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mfenced open=¨|¨ close=¨|¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«/mfenced»«mi»max«/mi»«/msub»«mo»=«/mo»«mn»4«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»2«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi»§#1043;§#1085;«/mi»«mo»§#183;«/mo»«mfrac»«mfenced open=¨|¨ close=¨|¨»«mrow»«mo»-«/mo»«mn»20«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«/mrow»«/mfenced»«mrow»«mn»2«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1089;«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mn»0«/mn»«mo»,«/mo»«mn»40«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1042;«/mi»«mo».«/mo»«/math»
Ответ: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mfenced open=¨|¨ close=¨|¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«/mfenced»«mi»max«/mi»«/msub»«/math» = 0,40 В.
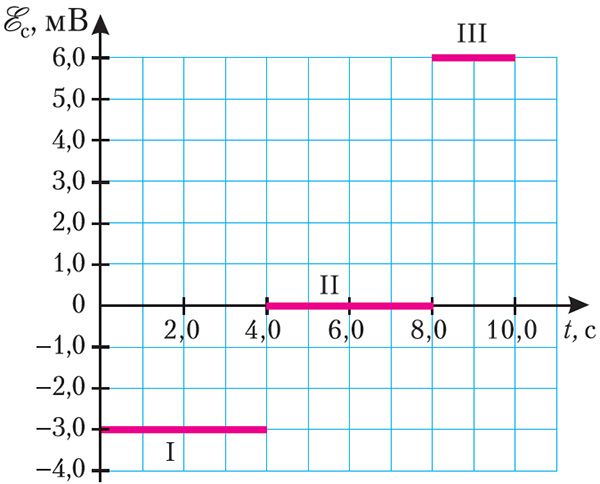
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔIIII — ? Wм — ?
Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi»§#1089;I«/mi»«/msub»«/math» = –3,0 мВ, на участке III — «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi»§#1089;III«/mi»«/msub»«/math» = 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi»§#1089;«/mi»«/msub»«mo»=«/mo»«mo»-«/mo»«mi»L«/mi»«mfrac»«mrow»«mo»§#8710;«/mo»«mi»I«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«/math»; «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«mi»I«/mi»«mo»=«/mo»«mo»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨script¨»E«/mi»«mi»§#1089;«/mi»«/msub»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«mi»L«/mi»«/mfrac»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«msub»«mi»I«/mi»«mi mathvariant=¨normal¨»I«/mi»«/msub»«mo»=«/mo»«mo»-«/mo»«mfrac»«mrow»«mo»-«/mo»«mn»3«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1042;«/mi»«mo»§#183;«/mo»«mn»4«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1089;«/mi»«/mrow»«mrow»«mn»2«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi»§#1043;§#1085;«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mn»6«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«/math»; «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«msub»«mi»I«/mi»«mi»III«/mi»«/msub»«mo»=«/mo»«mo»-«/mo»«mfrac»«mrow»«mn»6«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1042;«/mi»«mo»§#183;«/mo»«mn»2«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1089;«/mi»«/mrow»«mrow»«mn»2«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi»§#1043;§#1085;«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mo»-«/mo»«mn»6«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«/math».
На участке II графика «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mrow»«mi»§#1089;«/mi»«mi»II«/mi»«/mrow»«/msub»«/math» = 0, следовательно, сила тока не изменялась: ΔIII = 0.
В момент времени t = 4,0 с энергия магнитного поля катушки «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»W«/mi»«mi mathvariant=¨normal¨»§#1084;«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«mi»L«/mi»«msup»«mi»I«/mi»«mn»2«/mn»«/msup»«/mrow»«mn»2«/mn»«/mfrac»«/math».
Следовательно,
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»W«/mi»«mi mathvariant=¨normal¨»§#1084;«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«mn»2«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi»§#1043;§#1085;«/mi»«mo»§#183;«/mo»«msup»«mfenced»«mrow»«mn»6«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«/mrow»«/mfenced»«mn»2«/mn»«/msup»«/mrow»«mn»2«/mn»«/mfrac»«mo»=«/mo»«mn»36«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi»§#1044;§#1078;«/mi»«mo»=«/mo»«mn»36«/mn»«mo»§#160;«/mo»«mi»§#1084;§#1044;§#1078;«/mi»«/math».
Ответ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
![]()
Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I1 = 1,60 А до I2 = 2,40 А. При этом в катушке возникала ЭДС самоиндукции «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«/math» = ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.
Δt = 9,50 мс = 9,50 · 10-3 с
I1 = 1,60 А
I2 = 2,40 А
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«/math» = ‒14,0 В
ΔWм — ?
Решение: При изменении в катушке силы тока от I1 до I2 возникает собственный магнитный поток Фс = LI2. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»=«/mo»«mo»-«/mo»«mi»L«/mi»«mfrac»«mrow»«mo»§#8710;«/mo»«mi»I«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mo»-«/mo»«mi»L«/mi»«mfrac»«mrow»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«mo»-«/mo»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«/math». Следовательно,
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»L«/mi»«mo»=«/mo»«mo»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«mrow»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«mo»-«/mo»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«/mrow»«/mfrac»«mo»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«mrow»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«mo»-«/mo»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«/mrow»«/mfrac»«/math». Тогда «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨normal¨»§#1060;«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»§#8710;«/mo»«mi»t«/mi»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«mo»-«/mo»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«/mrow»«/mfrac»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨normal¨»§#1060;«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«mo»-«/mo»«mn»14«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1042;«/mi»«mo»§#183;«/mo»«mn»9«/mn»«mo»,«/mo»«mn»50«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1089;«/mi»«mo»§#183;«/mo»«mn»2«/mn»«mo»,«/mo»«mn»40«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«/mrow»«mrow»«mn»1«/mn»«mo»,«/mo»«mn»60«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«mo»-«/mo»«mn»2«/mn»«mo»,«/mo»«mn»40«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mn»0«/mn»«mo»,«/mo»«mn»399«/mn»«mo»§#160;«/mo»«mi»§#1042;§#1073;«/mi»«mo»=«/mo»«mn»399«/mn»«mo»§#160;«/mo»«mi»§#1084;§#1042;§#1073;«/mi»«mo».«/mo»«/math»
Приращение энергии магнитного поля катушки
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«msub»«mi»W«/mi»«mi mathvariant=¨normal¨»§#1084;«/mi»«/msub»«mo»=«/mo»«msub»«mi»W«/mi»«mrow»«mi mathvariant=¨normal¨»§#1084;«/mi»«mn»2«/mn»«/mrow»«/msub»«mo»-«/mo»«msub»«mi»W«/mi»«mrow»«mi mathvariant=¨normal¨»§#1084;«/mi»«mn»1«/mn»«/mrow»«/msub»«mo»=«/mo»«mfrac»«mrow»«mi»L«/mi»«msubsup»«mi»I«/mi»«mn»2«/mn»«mn»2«/mn»«/msubsup»«/mrow»«mn»2«/mn»«/mfrac»«mo»-«/mo»«mfrac»«mrow»«mi»L«/mi»«msubsup»«mi»I«/mi»«mn»1«/mn»«mn»2«/mn»«/msubsup»«/mrow»«mn»2«/mn»«/mfrac»«mo»=«/mo»«mfrac»«mi»L«/mi»«mn»2«/mn»«/mfrac»«mfenced»«mrow»«msubsup»«mi»I«/mi»«mn»2«/mn»«mn»2«/mn»«/msubsup»«mo»-«/mo»«msubsup»«mi»I«/mi»«mn»1«/mn»«mn»2«/mn»«/msubsup»«/mrow»«/mfenced»«mo»=«/mo»«mfrac»«mrow»«mo»-«/mo»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»§#8710;«/mo»«mi»t«/mi»«mfenced»«mrow»«msubsup»«mi»I«/mi»«mn»2«/mn»«mn»2«/mn»«/msubsup»«mo»-«/mo»«msubsup»«mi»I«/mi»«mn»1«/mn»«mn»2«/mn»«/msubsup»«/mrow»«/mfenced»«/mrow»«mrow»«mn»2«/mn»«mfenced»«mrow»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«mo»-«/mo»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«/mrow»«/mfenced»«/mrow»«/mfrac»«mo»=«/mo»«mfrac»«mrow»«mo»-«/mo»«msub»«mi mathvariant=¨script¨»E«/mi»«mi mathvariant=¨normal¨»§#1089;«/mi»«/msub»«mo»§#8710;«/mo»«mi»t«/mi»«mfenced»«mrow»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«mo»+«/mo»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«/mrow»«/mfenced»«/mrow»«mn»2«/mn»«/mfrac»«mo».«/mo»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«msub»«mi»W«/mi»«mi mathvariant=¨normal¨»§#1084;«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«mo»-«/mo»«mfenced»«mrow»«mo»-«/mo»«mn»14«/mn»«mo»,«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1042;«/mi»«/mrow»«/mfenced»«mo»§#183;«/mo»«mn»9«/mn»«mo»,«/mo»«mn»50«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»3«/mn»«/mrow»«/msup»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1089;«/mi»«mo»§#183;«/mo»«mo»(«/mo»«mn»2«/mn»«mo»,«/mo»«mn»40«/mn»«mo»§#160;«/mo»«mi mathvariant=¨normal¨»§#1040;«/mi»«mo»+«/mo»«mn»1«/mn»«mo»,«/mo»«mn»60«/mn»«mi mathvariant=¨normal¨»§#1040;«/mi»«mo»)«/mo»«/mrow»«mn»2«/mn»«/mfrac»«mo»=«/mo»«mn»0«/mn»«mo»,«/mo»«mn»266«/mn»«mo»§#160;«/mo»«mi»§#1044;§#1078;«/mi»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mn»266«/mn»«mo»§#160;«/mo»«mi»§#1084;§#1044;§#1078;«/mi»«mo».«/mo»«/math»
Ответ: Фс = 399 мВб, ΔWм = 266 мДж.