§ 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током |
| Напечатано:: | Гость |
| Дата: | Saturday, 6 December 2025, 00:44 |
Фарадей опытным путём установил, что электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797–1878) независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Каков механизм возникновения ЭДС индукции в этом случае?
Самоиндукция. Если электрический ток, проходящий в замкнутом проводящем контуре, по каким-либо причинам изменяется, то изменяется и магнитное поле, создаваемое этим током. Это влечёт за собой изменение магнитного потока через поверхность, ограниченную контуром. Поскольку магнитный поток Ф пропорционален модулю магнитной индукции В поля, который, в свою очередь, пропорционален силе тока I в контуре, то
Коэффициенту пропорциональности между магнитным потоком Ф и силой тока I Томсон (лорд Кельвин) в 1853 г. предложил название «коэффициент самоиндукции»:
Ф = LI.
(33.1)
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб. Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.
Если электрический ток, проходящий в контуре, изменяется, то он создаёт изменяющийся магнитный поток, что приводит к появлению ЭДС индукции. Это явление назвали самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи.
Возникающую в этом случае ЭДС назвали электродвижущей силой самоиндукции. Согласно закону электромагнитной индукции,
Если индуктивность контура не изменяется во времени, т. е. L = const, то
Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции. Силу тока самоиндукции можно определить по закону Ома где R — сопротивление контура. Согласно правилу Ленца, ток самоиндукции всегда направлен так, чтобы противодействовать изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.
Какой должна быть скорость изменения силы тока, чтобы в катушке с индуктивностью L = 0,20 Гн возникла ЭДС самоиндукции = 4,0 В?
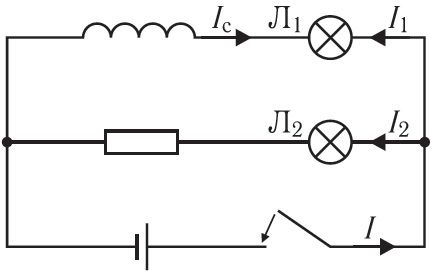
Наблюдение самоиндукции. Для наблюдения явления самоиндукции соберём электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока. Схема цепи представлена на рисунке 185. При замыкании ключа лампочка Л2 начинает светиться практически сразу, а лампочка Л1 — с заметным запаздыванием. При возрастании силы тока I1, созданного источником на участке, образованном катушкой и лампочкой Л1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции Iс направлен навстречу току источника. В результате рост силы тока I1 источника замедляется, и сила тока I1 — |Iс| не сразу достигает своего максимального значения.
![]()
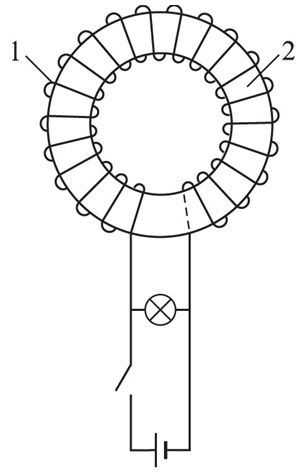
Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Соберём цепь, состоящую из катушки с большим количеством витков 1, намотанных на железный сердечник 2, к зажимам которой подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки (рис. 185.1). В качестве источника тока возьмём источник, ЭДС которого 2 В. Лампочка подключена параллельно катушке. При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединённых катушки и лампочки.
Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений . Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки. Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.
![]()
Энергия магнитного поля. Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.
При замыкании цепи, состоящей из источника тока с ЭДС , катушки с индуктивностью L и резистора, сопротивление которого R, сила тока в цепи начнёт возрастать и появится ЭДС самоиндукции
.
Тогда в соответствии с законом Ома сила тока в цепи .
Значит, .
Умножив полученное равенство на IΔt, где Δt — достаточно малый промежуток времени, в течение которого сила тока I остаётся практически постоянной, найдём элементарную работу, совершаемую сторонними силами в источнике тока: .
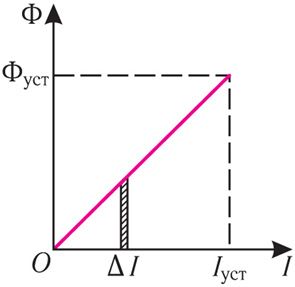
В процессе установления тока, когда сила тока I и магнитный поток Ф = LI возрастают, работа, совершаемая сторонними силами в источнике тока, превышает выделяющееся в резисторе количество теплоты. Элементарная дополнительная работа, совершаемая сторонними силами за промежуток времени Δt при преодолении ЭДС самоиндукции в процессе установления тока (рис. 185.2):
δAдоп = ФΔI.
Полная дополнительная работа Адоп, равная сумме элементарных дополнительных работ δAдоп в процессе установления тока, равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости Ф = Ф(I) (см. рис. 185.2).
Эта работа превращается в энергию магнитного поля катушки, поэтому:
где L — индуктивность контура; I — сила тока.
Какова индуктивность катушки, если при силе тока I = 2,0 А энергия магнитного поля катушки Wм = 1,2 Дж?

1. Что называют самоиндукцией?
2. В каких опытах можно наблюдать явление самоиндукции?
3. От чего зависит ЭДС самоиндукции?
4. Что называют индуктивностью? В каких единицах в СИ её измеряют?
5. Как вычислить энергию магнитного поля катушки с током?
![]()
6. Почему для создания электрического тока в цепи с катушкой индуктивности источник тока должен затратить энергию?
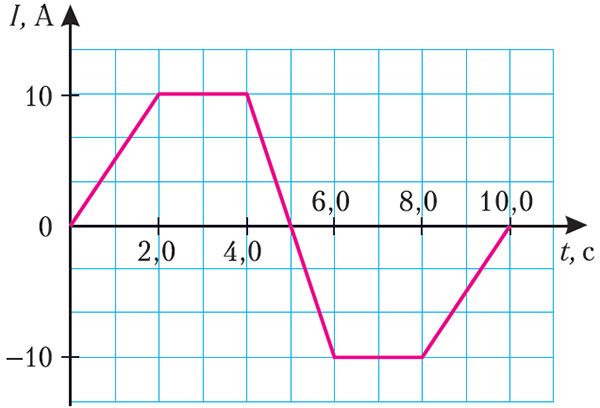
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.
L = 40 мГн = 4,0 · 10–2 Гн
Решение: ЭДС самоиндукции . Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:
1) от момента времени t1 = 0,0 с до момента времени t2 = 2,0 с сила тока изменяется на ΔI1 = 10 А за промежуток времени Δt1 = 2,0 с;
2) от момента времени t3 = 4,0 с до момента времени t4 = 6,0 с сила тока изменяется на ΔI2 = –20 А за промежуток времени Δt2 = 2,0 с;
3) от момента времени t5 = 8,0 с до момента времени t6 = 10,0 с сила тока изменяется на ΔI3 =10 А за промежуток времени Δt3 = 2,0 с.
Поскольку промежутки времени Δt1 = Δ t2 = Δ t3 = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt2 = 2,0 с (от t3 = 4,0 с до t4 = 6,0 с):
Таким образом,
Ответ: = 0,40 В.
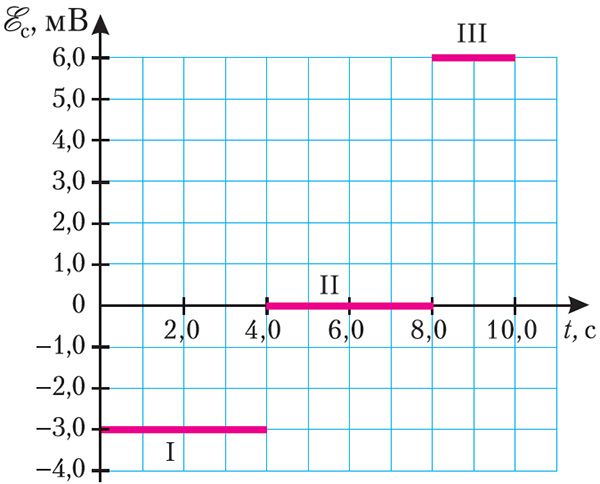
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔIIII — ? Wм — ?
Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции = –3,0 мВ, на участке III —
= 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:
;
.
;
.
На участке II графика = 0, следовательно, сила тока не изменялась: ΔIII = 0.
В момент времени t = 4,0 с энергия магнитного поля катушки .
Следовательно,
.
Ответ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
![]()
Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I1 = 1,60 А до I2 = 2,40 А. При этом в катушке возникала ЭДС самоиндукции = ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.
Δt = 9,50 мс = 9,50 · 10-3 с
I1 = 1,60 А
I2 = 2,40 А
ΔWм — ?
Решение: При изменении в катушке силы тока от I1 до I2 возникает собственный магнитный поток Фс = LI2. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: . Следовательно,
. Тогда
.
Приращение энергии магнитного поля катушки
Ответ: Фс = 399 мВб, ΔWм = 266 мДж.
Упражнение 24
1. Сила тока, проходящего по замкнутому проводящему контуру, I = 1,2 А. Магнитное поле этого тока создаёт магнитный поток Ф = 3,0 мВб через поверхность, ограниченную контуром. Определите индуктивность контура.
2. При равномерном изменении силы тока в катушке на ΔI = –4,0 А за промежуток времени Δt = 0,10 с в ней возникает ЭДС самоиндукции = 20 В. Определите индуктивность катушки.
3. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 1,2 Гн, при равномерном изменении силы тока от I1 = 2,0 А до I2 = 6,0 А за промежуток времени Δt = 0,60 с. Определите приращение энергии магнитного поля при заданном изменении силы тока.
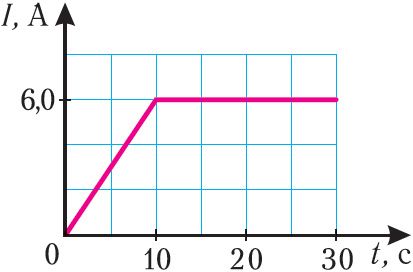
4. На рисунке 188 представлен график зависимости силы тока в катушке, индуктивность которой L = 10 мГн, от времени. Определите ЭДС самоиндукции через промежутки времени t1 = 10 с и t2 = 20 с от момента начала отсчёта времени.
5. Сила тока в катушке равномерно уменьшилась от I1 = 10 А до I2 = 5,0 А. При этом энергия магнитного поля изменилась на ΔWм = –3,0 Дж. Определите индуктивность катушки и первоначальное значение энергии магнитного поля.
6. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 0,12 Гн, при равномерном уменьшении силы тока от I1 = 8,0 А, если за промежуток времени t1 = 0,20 с энергия магнитного поля уменьшилась в α = 2,0 раза.
![]()
7. Энергия магнитного поля катушки с индуктивностью L1 = 0,5 Гн больше энергии магнитного поля катушки с индуктивностью L2 в α = 1,5 раза. Определите индуктивность второй катушки, если отношение собственного магнитного потока через поверхности, ограниченные витками второй катушки, к собственному магнитному потоку через поверхности, ограниченные витками первой катушки, .

