§ 14. Моделирование в экономических задачах

14.2. Задача оптимального планирования производства

Задача 1. Кондитерский цех выпускает два вида тортов: «Лакомка» и «Медовый». На изготовление торта «Лакомка» затрачивается в среднем 0,3 ч, а на изготовление торта «Медовый» — 0,4 ч. Рабочий день длится 8 ч. Для хранения готовой продукции в цехе имеется холодильник на 25 тортов. Торт «Лакомка» продается по цене 12 руб., а торт «Медовый» — по цене 15 руб. Каким должен быть дневной план производства тортов, чтобы объем производства в денежном выражении был максимальным?

По перечню этапов моделирования этап постановки задачи 1 (этап 1) пройден. На этапе 2 следует выбрать план создания модели (пример 14.3). Для создания математической модели (этап 3а) введем величину x для обозначения количества тортов «Лакомка», планируемых для изготовления за день, и аналогично величину y для обозначения количества тортов «Медовый». Тогда пара (x, y) является планом кондитерского цеха на день, а величины x и y — плановыми показателями.

Обозначим через U(x, y) объем дневного производства тортов в денежном выражении (пример 14.4).

Ограничения на ресурсы связаны с ограниченным числом мест для хранения готовой продукции (пример 14.5) и ограничениями на время изготовления продукции (пример 14.6). Ограничения затрагивают и значения плановых показателей (пример 14.7).

Решением данной задачи оптимального планирования производства является такая пара плановых показателей (x, y), которая удовлетворяет ограничениям:

x + y ≤ 25,
0,3x + 0,4 ≤  8
x, y  — целые,
x ≥ 0, y ≥ 0,

а функция U(x, y) = 12x + 15y принимает максимальное значение.

Получаем следующую математическую задачу нахождения максимума функции при ограничениях:

U(x, y) → max;
x + y ≤ 25,
0,3x + 0,4y ≤ 8
x, y  — целые,
x ≥ 0, y ≥ 0.

Такие задачи называются экстремальными. В экстремальных задачах функция, для которой ищется максимум или минимум называется целевой функцией, обозначение max (максимум) называется критерием. Методы решения экстремальных задач реализованы в электронных таблицах Excel с помощью надстройки Поиск решения (пример 14.8).

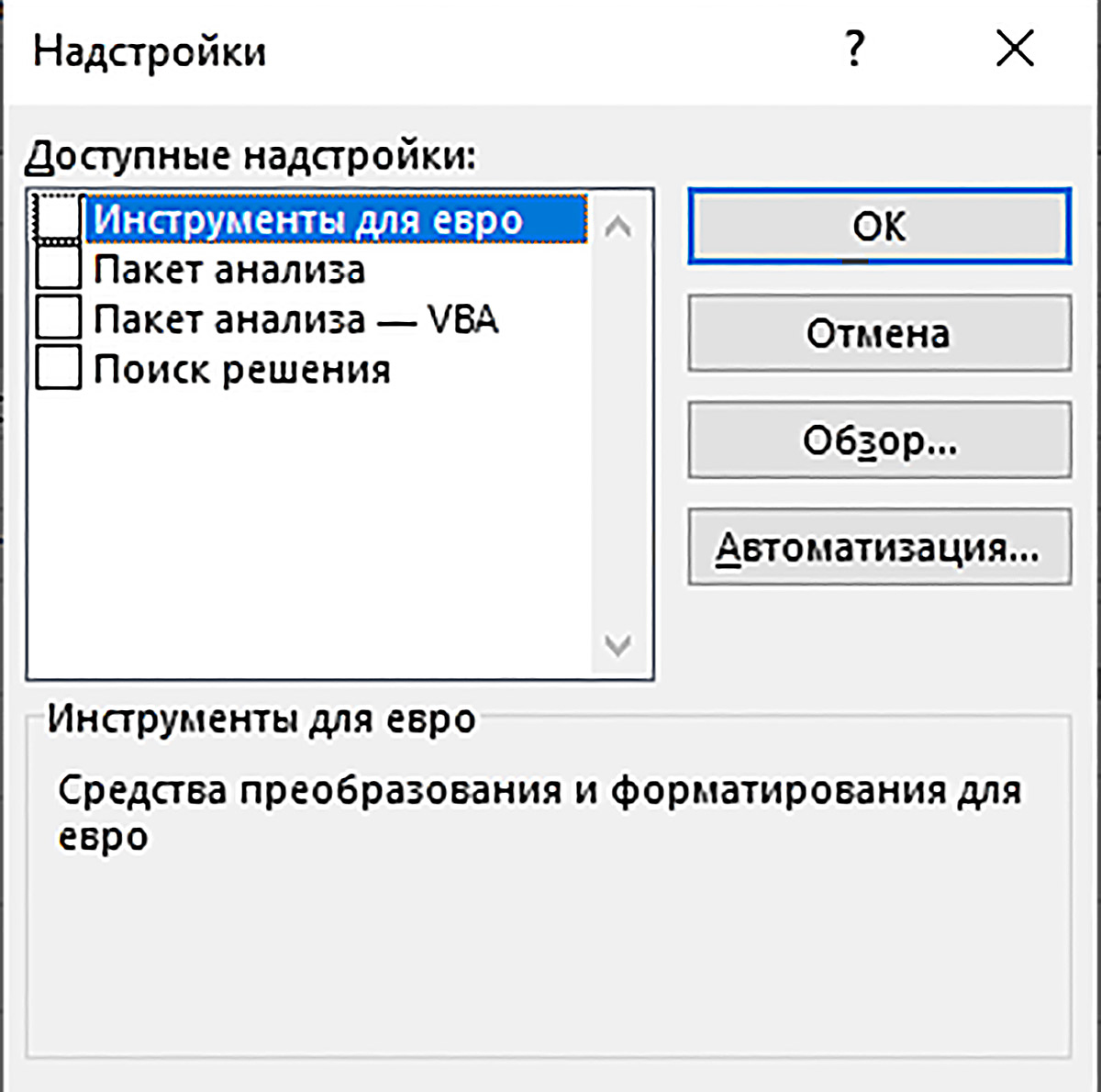
Пример 14.3. На этапе 2 изберем следующий план решения задачи 1 оптимального планирования производ­ства: этап 3а — создание документальной математичес­кой модели; этап 3б — создание компьютерной расчетной модели.

Пример 14.4. По исходным данным задачи 1 выражение для объема производства в денежном выражении легко находится:

U(x, y) = 12x + 15y.

Пример 14.5. Ограничение на число мест в холодильнике выражается неравенством

x + y ≤ 25.

Пример 14.6. На изготовление одного торта «Лакомка» в среднем уходит 0,3 ч, а на изготовление одного торта «Медовый» — 0,4 ч. Тогда на изготовление тортов по плану (x, y) будет затрачено 0,3x + 0,4y (ч).

Учитывая длительность рабочего дня, получаем ограничение

0,3x + 0,4y ≤ 8.

Пример 14.7. В задаче речь идет о тортах. Такую продукцию называют штучной, так как она учитывается поштучно. Поэтому решением задачи могут быть только целые значения плановых показателей. Получаем ограничение

x, y  — целые.

Так как в результате вычислений могут получиться и отрицательные числа, то следует ограничить значения плановых показателей неравенствами

x ≥ 0, y ≥ 0.

Пример 14.8. При установке программы Excel ее надстройки автоматически не устанавливаются.

Для установки надстройки Поиск решения следует на вкладке Файл в левом вертикальном меню выбрать пункт Параметры. Открывается диалоговое окно Параметры.

В левом вертикальном меню этого диалогового окна выбирают пункт Надстройки. Открывается вкладка Надстройки.

На вкладке Надст­ройки в ее последнем разделе Управление: размещено поле, в котором должна находиться надпись Надстройки Excel.

Правее надписи в текстовом поле щелкают по кнопке Перейти … . Появляется еще одно диалоговое окно Надстройки.

В окне Надстройки отмечают пункт Поиск решения и щелкают по кнопке ОK. Надстройка Поиск решения устанавливается.