§ 14. Моделирование в экономических задачах
| Сайт: | Профильное обучение |
| Курс: | Информационные технологии. 11 класс (Базовый уровень) |
| Книга: | § 14. Моделирование в экономических задачах |
| Напечатано:: | Гость |
| Дата: | Tuesday, 14 October 2025, 14:59 |
14.1. Основные понятия
|
Экономическая модель — это формализованное описание экономического объекта, процесса или явления. Целями моделирования в экономике являются: анализ экономических объектов, процессов и явлений, предсказание параметров развития экономических процессов (прогнозирование), подготовка управленческих решений на всех уровнях экономики. В экономике широко используются модели различной сложности, начиная от простых структурных схем (пример 14.1). Если экономическая модель использует математические понятия и математический аппарат, то такую модель часто называют экономико-математической моделью (пример 14.2). При решении сложных практических задач экономико-математические модели обычно включают наборы уравнений и неравенств. Рассмотрим подробнее моделирование при решении задач оптимального планирования. Задача оптимального планирования заключается в определении таких значений плановых показателей хозяйственного объекта, которые обеспечат достижение поставленной цели с учетом ограниченности ресурсов. |
Пример 14.1. Предметом микроэкономики является фирма, ее внутренняя и внешняя среда, что хорошо описывает модель-схема. Пример 14.2. Простейшей формой экономико-математической модели является график. Примером является широко известная модель спроса S и предложения D в системе координат Q (количество товара) и P (цена за этот товар). Модель позволяет находить точку равновесия спроса и предложения E и равновесную цену P0. |
14.2. Задача оптимального планирования производства
|
Задача 1. Кондитерский цех выпускает два вида тортов: «Лакомка» и «Медовый». На изготовление торта «Лакомка» затрачивается в среднем 0,3 ч, а на изготовление торта «Медовый» — 0,4 ч. Рабочий день длится 8 ч. Для хранения готовой продукции в цехе имеется холодильник на 25 тортов. Торт «Лакомка» продается по цене 12 руб., а торт «Медовый» — по цене 15 руб. Каким должен быть дневной план производства тортов, чтобы объем производства в денежном выражении был максимальным? По перечню этапов моделирования этап постановки задачи 1 (этап 1) пройден. На этапе 2 следует выбрать план создания модели (пример 14.3). Для создания математической модели (этап 3а) введем величину x для обозначения количества тортов «Лакомка», планируемых для изготовления за день, и аналогично величину y для обозначения количества тортов «Медовый». Тогда пара (x, y) является планом кондитерского цеха на день, а величины x и y — плановыми показателями. Обозначим через U(x, y) объем дневного производства тортов в денежном выражении (пример 14.4). Ограничения на ресурсы связаны с ограниченным числом мест для хранения готовой продукции (пример 14.5) и ограничениями на время изготовления продукции (пример 14.6). Ограничения затрагивают и значения плановых показателей (пример 14.7). Решением данной задачи оптимального планирования производства является такая пара плановых показателей (x, y), которая удовлетворяет ограничениям: x + y ≤ 25, а функция U(x, y) = 12x + 15y принимает максимальное значение. Получаем следующую математическую задачу нахождения максимума функции при ограничениях: U(x, y) → max; |
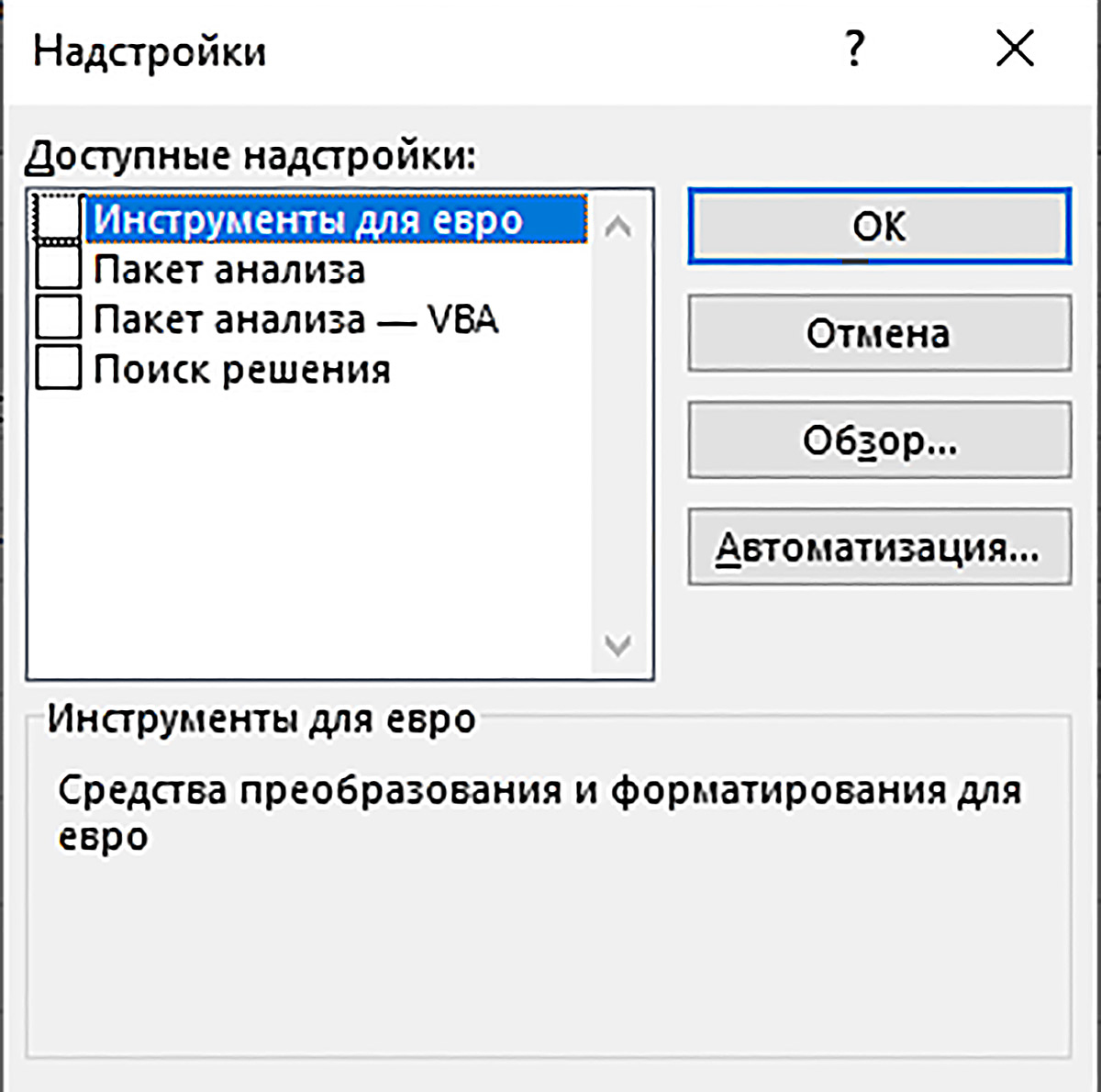
Пример 14.3. На этапе 2 изберем следующий план решения задачи 1 оптимального планирования производства: этап 3а — создание документальной математической модели; этап 3б — создание компьютерной расчетной модели. Пример 14.4. По исходным данным задачи 1 выражение для объема производства в денежном выражении легко находится: U(x, y) = 12x + 15y. Пример 14.5. Ограничение на число мест в холодильнике выражается неравенством x + y ≤ 25. Пример 14.6. На изготовление одного торта «Лакомка» в среднем уходит 0,3 ч, а на изготовление одного торта «Медовый» — 0,4 ч. Тогда на изготовление тортов по плану (x, y) будет затрачено 0,3x + 0,4y (ч). Учитывая длительность рабочего дня, получаем ограничение 0,3x + 0,4y ≤ 8. Пример 14.7. В задаче речь идет о тортах. Такую продукцию называют штучной, так как она учитывается поштучно. Поэтому решением задачи могут быть только целые значения плановых показателей. Получаем ограничение x, y — целые. Так как в результате вычислений могут получиться и отрицательные числа, то следует ограничить значения плановых показателей неравенствами x ≥ 0, y ≥ 0. Пример 14.8. При установке программы Excel ее надстройки автоматически не устанавливаются. Для установки надстройки Поиск решения следует на вкладке Файл в левом вертикальном меню выбрать пункт Параметры. Открывается диалоговое окно Параметры. В левом вертикальном меню этого диалогового окна выбирают пункт Надстройки. Открывается вкладка Надстройки. На вкладке Надстройки в ее последнем разделе Управление: размещено поле, в котором должна находиться надпись Надстройки Excel. Правее надписи в текстовом поле щелкают по кнопке Перейти … . Появляется еще одно диалоговое окно Надстройки. В окне Надстройки отмечают пункт Поиск решения и щелкают по кнопке ОK. Надстройка Поиск решения устанавливается. |
14.3. Построение компьютерной расчетной модели
|
На этапе 3б моделирования простроим в электронных таблицах компьютерную расчетную модель с исходными данными задачи 1. Данные компьютерной модели разместим по схеме, приведенной в примере 14.9. Вводим формулы A12: =B11+C11 A13: =B4*B11+C4*C11 A14: =B5*B11+C5*C11 |
14.4. Работа с надстройкой «Поиск решения»
|
На 4 и 5 этапах моделирования используем надстройку Поиск решения. Надстройка Поиск решения вызывается на вкладке Данные в группе Анализ инструментом Поиск решения. Появляется диалоговое окно Параметры поиска решения (пример 14.10). В поле первой строки следует ввести ссылку на ячейку со значением целевой функции. Если там есть данные, то их удаляем и щелкаем по ячейке A14. В строке До: должен быть выбран критерий Максимум. В поле ввода Изменяя ячейки переменные: вводим диапазон B11:C11, выделяя его в таблице протяжкой мыши. Далее нужно ввести ограничения задачи в большое поле В соответствии с ограничениями: (пример 14.11). Под полем для ограничений ставим галочку выбора условия Сделать переменные без ограничений неотрицательными. В поле Выберите метод решения: необходимо выбрать Поиск решения задач лин. симплекс методом. Когда параметры поиска введены, нужно щелкнуть по кнопке Найти решение в нижней части диалогового окна. Расчет проводится практически мгновенно. В разделе Результаты модели появляются искомые значения плановых показателей. Также появляется окно Результаты поиска решения, в котором предлагаются способы сохранения данных на листе книги Excel. Осталось проверить адекватность модели на контрольных данных (пример 14.12). |
Пример 14.10. Верхняя часть диалогового окна Параметры поиска решения: Пример 14.11. Справа от поля В соответствии с ограничениями: нажимаем кнопку Добавить. Появляется окно для ввода ограничений. Щелкаем в левом поле, потом по ячейке A12 таблицы, в среднем окне оставляем знак неравенства, щелкаем по правому полю, затем по ячейке A6. В завершение щелкаем по кнопке OK. Аналогично вводим второе ограничение со ссылкой на ячейку A13 и ограничением в ячейке A7. Чтобы значения ячеек диапазона B11:C11 стали целыми числами, следует в диалоговом окне Добавление ограничений слева ввести диапазон, а центральном поле выбрать обозначение «цел». Пример 14.12. Контрольные данные для проверки адекватности модели по исходным данным задачи 1 включают: * плановые показатели (20 тортов «Лакомка» и 5 тортов «Медовый»); * время производства 8 ч; * объем производства 315 руб. |
14.5. Задача оптимального планирования времени производства
|
Задача 2. Кондитерский цех выпускает два вида тортов: «Лакомка» и «Медовый». На изготовление торта «Лакомка» затрачивается в среднем 0,3 ч, а на изготовление торта «Медовый» — 0,4 ч. Для хранения готовой продукции в цехе имеется холодильник на 25 тортов. Торт «Лакомка» продается по цене 12 руб., а торт «Медовый» — по цене 15 руб. Каким должен быть план производства, чтобы заказ стоимостью не менее 150 руб. был выполнен за минимальное время? Поставленная здесь задача 2 сохранила исходные данные задачи 1. Однако вопрос к задаче 2 содержит новое ограничение и новую цель производства: следует выполнить заказ за минимальное время. Для построения документальной математической модели сохраним обозначения задачи 1. Новой будет целевая функция — время производства (время выполнения заказа): T(x, y) =0,3x + 0,4y → min Останутся ограничения x + y ≤ 25, Добавится ограничение на объем производства (заказа) в денежном выражении U(x, y) = 12x + 15y ≥ 150. Для создания компьютерной расчетной модели можно изменить модель, построенную для решения задачи 1 (пример 14.13). Для проведения расчетов вызываем диалоговое окно Параметры поиска решения (пример 14.14). |
Пример 14.13. На новый лист рабочей книги электронных таблиц вставим копию компьютерной расчетной модели, построенной для решения задачи 1. Для этого открываем лист с компьютерной моделью задачи 1 оптимального планирования производства. Щелкнув по кнопке над заголовком первой строки таблицы, выделяем весь лист и копируем его в буфер обмена любым способом. Затем открываем новый лист рабочей книги, также выделяем его весь и вставляем скопированный лист каким угодно способом. Меняем часть заголовка модели. В ячейку B8 вводим текст «: объем заказа (в рублях)», а в ячейку A8 — число 150. Пример 14.14. В диалоговом окне Параметры поиска решения в поле Оптимизировать целевую функцию: необходимо внести ссылку на ячейку A13, выбрать критерий — Минимум, ввести диапазон изменяемых ячеек — B11:C11. Далее следует ввести ограничения: A12 ≤ A6, A14 ≥ A8, B11:C11 = целое. Под полем для ограничений должна стоять галочка выбора условия Сделать переменные без ограничений неотрицательными. Выбираем метод решения Поиск решения лин. задач симплекс-методом. Щелчок по кнопке Найти решение запускает процесс решения задачи. Адекватность модели проверяется сравнением с контрольными данными: «Лакомка» — 10, «Медовый» — 2. |
Упражнения

1. Повторите на компьютере построение компьютерной расчетной модели для задачи1 оптимального планирования производства и поиск решения задачи.
2. На листе электронной таблицы с компьютерной моделью, построенной в упражнении 1, постройте таблицу со следующими столбцами:

Задав число мест хранения 20, найдите решение задачи и запишите в первую строку таблицы значения найденных плановых показателей и объема производства в денежном выражении. Аналогично заполните остальные строки таблицы для числа мест хранения от 21 до 30. Как связано число мест хранения в холодильнике с объемом производства в денежном выражении? Имеет ли смысл иметь в холодильнике более 26 мест хранения?
3. Решите следующую задачу. Цех мебельной фабрики выпускает детские мебельные наборы «Буслик» и «Гном». Для каждого набора «Буслик» требуется 0,2 ч машинного времени и 3,5 м2 мебельного щита, а для каждого набора «Гном» требуется 0,5 ч машинного времени и 4 м2 мебельного щита. В неделю можно использовать не более 150 ч машинного времени и не более 1600 м2 мебельных щитов. Набор «Буслик» продается по цене 130 руб., а набор «Гном» — по цене 200 руб. Сколько наборов каждого вида следует выпускать в неделю для достижения максимального объема производства в денежном выражении? Ответ: 210; 216.
4. Повторите на компьютере построение компьютерной расчетной модели для задачи 2 оптимального планирования времени производства и поиск решения задачи.
5. Решите следующую задачу. Цех мебельной фабрики выпускает детские мебельные наборы «Буслик» и «Гном». Для каждого набора «Буслик» требуется 0,2 ч машинного времени и 3,5 м2 мебельного щита, а для каждого набора «Гном» требуется 0,5 ч машинного времени и 4 м2 мебельного щита. В неделю можно использовать не более 1600 м2 мебельных щитов. Набор «Буслик» продается по цене 130 руб., а набор «Гном» — по цене 200 руб. Сколько наборов каждого вида следует выпускать в неделю, чтобы объем производства в денежном выражении был не ниже 60 000 руб., а использование машинного времени было минимальным? Ответ: 442; 13.