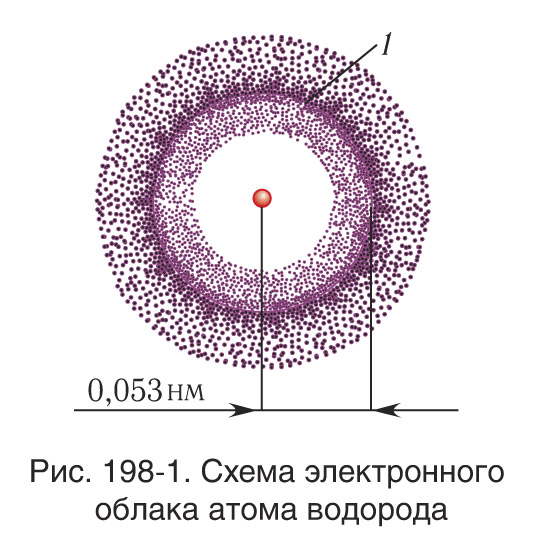
§ 31-1. Квантово-механическая модель атома
Теория Бора предложила физикам пользоваться по
понедельникам, средам и пятницам классическими законами,
а по вторникам, четвергам и субботам — квантовыми.
Вильям Брэгг-старший
|
Модель атома Бора не смогла дать исчерпывающие ответы на вопросы об устойчивости атома, о дискретности спектра его излучения. Только с развитием квантовой механики с использованием нового математического аппарата удалось построить завершенную модель строения атома, позволяющую понять законы микромира. |
Атомная орбиталь — область околоядерного пространства, в котором наиболее вероятно нахождение данного электрона (рис. 198-1). Орбитали, в зависимости от энергии электронов, имеют различные формы и размеры. Каждый электрон характеризуется собственным механическим моментом движения, который называется спином (от англ. spin — вращать), проекция которого принимает два значения. На одной орбитали может находиться не более двух электронов, имеющих противоположные (антипараллельные) спины.
В классической механике движение частицы описывается заданием ее координат и импульса (скорости) в каждой точке траектории. Чтобы рассчитать параметры движения любой сложной системы, достаточно задать координаты и импульсы (скорости) всех частиц, входящих в систему, в начальный момент времени и условия, при которых происходит движение (действующие силы, поля). После этого, используя уравнения движения (второй закон Ньютона), можно найти координаты и импульсы (скорости) в любой момент времени, т.е. определить, где будет находиться частица в тот или иной момент времени.
При переходе в область микромира оказывается, что такой способ не применим. Для описания явлений микромира была разработана квантовая механика. Квантовая механика — раздел физики, в котором изучаются свойства и поведение микрочастиц, а также связь величин, характеризующих частицы, с физическими величинами, непосредственно измеряемыми в экспериментах.
Результаты экспериментов показывают, что микрообъекты обладают одновременно корпускулярными и волновыми свойствами. Так, например, электрон является частицей, имеющей определенную массу и заряд, но при его движении вокруг ядра необходимо учитывать его волновые свойства, так как у него отсутствует определенная траектория движения и точное расположение в пространстве. Для объяснения двойственного поведения микрообъектов требовался кардинальный пересмотр установившихся представлений.
В квантовой механике движение частицы описывается волновой функцией — функцией координат и времени. Зная волновую функцию частицы, используя измерительные приборы, можно получить сведения о поведении этой частицы и о результатах любого ее взаимодействия. При этом волновая функция характеризует вероятность любого результата измерения. Квадрат ее модуля
определяет вероятность пребывания частицы в окрестности точки с координатами (x,y,z) в момент времени t. В квантовой механике, даже если задать все начальные условия в какой-то момент времени и полностью решить систему уравнений для волновых функций, можно установить только вероятность тех или иных процессов. Например, вероятность обнаружить электрон в данном месте может оказаться в 10 раз больше вероятности его нахождения в другом месте. Однако предсказать его положение со стопроцентной достоверностью, как это было в классической механике, уже нельзя.
Электроны в атоме приближенно рассматриваются как «размазанные» в пространстве и образующие вокруг ядра электронное облако (см. рис. 198-1). Электронное облако, которое соответствует основному состоянию, концентрируется в области, находящейся достаточно близко к ядру. Для возбужденных состояний оно распределяется на все большие расстояния от ядра. Слабее всего связаны с ядром электроны самой внешней оболочки, которые определяют размеры атома в целом.
В зависимости от того, что и как измеряется в определенном состоянии частицы, на первый план выступают то ее корпускулярные свойства, то ее волновые свойства. Применение волновой функции позволяет описать как корпускулярные, так и волновые свойства микрочастиц.
Важнейшим физическим положением квантовой механики является знаменитый принцип неопределенности Гейзенберга, согласно которому:
ни при каком увеличении точности измерений невозможно добиться того, чтобы произведение неопределенностей измерения координаты и импульса частицы стало меньше постоянной Планка.
Таким образом, в квантовой механике для системы, находящейся в некотором известном состоянии, можно предсказать результаты измерений либо ее положения, либо ее импульса по отдельности. Вероятностная интерпретация предсказывает, что измерения одинаковым детектором для одинаковых частиц в одинаковых состояниях одной и той же величины будут давать разные результаты. В частности, вероятность координаты определяется как .
Один из важнейших выводов квантовой механики состоит в том, что существует самый низкий уровень энергии, которому соответствует основное состояние системы. В этом состоянии система обладает минимальной кинетической энергией, причем ≠ 0.
Таблица 9-1. Квантовые числа |
|||
|
Квантовое число |
Символ |
Значения |
Полное число значений |
|
Главное |
n |
1,2,3 ... |
|
|
Орбитальное |
l |
0,1, ... , n - 1 |
n (при заданном n) |
|
Магнитное |
ml |
- l, - l + 1, ... l - 1 |
2l +1 (при заданном l) |
|
Спиновое |
ms |
|
2 |
Ядерная модель атома не означает, что существуют орбиты электронов и что электрон необходимо уподобить твердому шарику, движущемуся вокруг ядра. Отказ от такого механического представления об электроне и его движении позволил Гейзенбергу и Шредингеру построить квантовую теорию атома, в которой постулаты Бора оказываются следствиями более общих принципов.
В квантовой механике для задания каждого состояния электрона в атоме необходимы четыре различных квантовых числа n, l, ml, ms . В таблице 9-1 представлены допустимые значения всех четырех квантовых чисел электрона.
Рассмотрим основы квантово-механического описания наиболее простого атома — атома водорода. Квантовое число n из модели атома Бора сохраняется под названием главного квантового числа. Оно принимает целочисленные значения от 1 до . От него зависят полная энергия состояния атома водорода:
Число l называется орбитальным квантовым числом, которое (при заданном n) принимает целочисленные значения:
Число ml называется магнитным квантовым числом и принимает (при заданном l) целочисленные значения от -l до +l :
Для описания состояний электрона в атоме вводится еще одно квантовое число — спиновое , которое принимает два значения:
Это связано с тем, что при заданных n, l, ml электрон может находиться в двух различных состояниях, характеризуемых проекцией спина.
Австрийский физик-теоретик Вольфганг Паули предложил простое правило (принцип запрета Паули) — в одном и том же квантовом состоянии может находиться не более одного электрона.
 Согласно этому принципу два электрона не могут иметь одинакового набора квантовых чисел, и на его основе объясняется наличие групп из 2, 8, 18 и 32 элементов периодической таблицы Менделеева.
Согласно этому принципу два электрона не могут иметь одинакового набора квантовых чисел, и на его основе объясняется наличие групп из 2, 8, 18 и 32 элементов периодической таблицы Менделеева.
Эти группы элементов являются следствием принципа запрета Паули, а также квантово-механического правила, согласно которому значение квантового числа l не превосходит
n-1(0 ≤ l ≤ n-1), а квантовое число m пробегает ряд целочисленных значений от -l до +l (- l ≤ m ≤ + l).
Атом водорода может иметь одно и то же значение энергии, находясь в различных состояниях (рис. 198-2).
Энергия атома водорода зависит только от главного квантового числа n, но уровню энергии с заданным n соответствуют несколько состояний, отличающихся значениями l, ml, ms. Состояния с заданными значениями n, l принято обозначать как 1s, 2s, 2p, 3s, ... , где цифры указывают значения n, а буквы s,p,d,f, ... — соответствующие значения l = 0,1,2,3, ... . Уровень, которому соответствует лишь одно квантовое состояние, называется невырожденным.
Полное число всех возможных состояний электрона с различными l и m при фиксированном значении главного квантового числа n получится равным n2. С учетом двух возможных значений спина общее число электронов в оболочке оказывается равным 2n2. Это и есть максимальное число электронов в оболочке с номером n.
Спектр излучения (поглощения) атома водорода можно полностью описать как результат переходов атома из одних состояний, описываемого квантовыми числами n, l, ml, ms, в другие, описываемые иным набором. Однако, как доказано теоретически и подтверждено экспериментально, разрешены не все переходы, а только удовлетворяющие правилам отбора.
Правила отбора касаются изменений орбитального l и магнитного ms квантовых чисел при переходах с излучением (т.е. испусканием или поглощением). Их изменение удовлетворяет условиям:
В то же время правила отбора не накладывают никаких ограничений на изменения главного квантового числа n .
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число, называют электронной оболочкой или слоем.
Основные законы квантовой механики были открыты в 1900—1928 гг. В это же время произошло ее становление как новой науки — полноправного раздела теоретической физики. В это время были выдвинуты новые фундаментальные идеи — кванта энергии и света, стационарных состояний атомных систем и переходов между ними, принципа соответствия и корпускулярно-волнового дуализма для излучения и микрочастиц.
Решив задачу описания простейшего из атомов — атома водорода, квантовая механика в настоящее время применяется для решения разнообразных проблем физики микроскопических явлений — в теории атомов и молекул, ядер, элементарных частиц, в теории столкновений и теории излучения. Как было установлено, квантовые свойства частиц проявляются в таких физических явлениях, как сверхпроводимость, ферромагнетизм, сверхтекучесть.
Принцип неопределенности Гейзенберга математически выражается в виде следующего неравенства, связывающего неопределенность координаты x с неопределенностью
проекции импульса
:
,
которое обычно называют соотношением неопределенностей Гейзенберга. По представлениям Бора, координаты и импульсы подобны двум проекциям предмета, который может быть сфотографирован либо спереди, либо сбоку, но не сразу со всех сторон. Они не отвергают, а дополняют друг друга.
В
|
В В В 1954 г. М. Борн был удостоен Нобелевской премии за фундаментальные исследования в квантовой механике, в особенности за статистическую интерпретацию волновой функции |
 |