§ 26. Алгебра логики
26.1. Логические высказывания
|
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. Для того чтобы иметь представление об устройстве компьютера, необходимо познакомиться не только с арифметическими, но и с основными логическими элементами, лежащими в основе его построения. Для понимания принципа работы таких элементов рассмотрим основные понятия алгебры логики. Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях. Аналогию между алгеброй и логикой положил в основу своего логического учения основоположник алгебры логики английский математик и логик Дж. Буль (1815–1864). Любое высказывание Буль записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов. Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно — 1 или ложно — 0. Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения. Истинность или ложность высказываний зависит от истинности и ложности исходных (простых) высказываний и смысла логических операций над высказываниями (пример 26.1). Таким образом, определение истинности некоторого логического выражения — это определение значения некоторой логической функции. Логическая функция — функция, принимающая значения 0 или 1 в результате логических операций над логическими переменными. Способы задания логической функции: 1) словесное описание; 2) таблица истинности; 3) формула, записанная с помощью букв, знаков логических операций и скобок; 4) комбинационная схема, составленная из логических элементов; 5) координатный способ (карта Карно); 6) диаграмма Венна (Эйлера). Области применения алгебры логики: 1) в качестве средства алгоритмического описания в языках программирования для определения логических условий; 2) для формирования логических высказываний в математической логике, лингвистике, теории искусственного интеллекта; 3) в разработке и описании дискретных технических систем; 4) при анализе и синтезе логических устройств. |
Пример 26.1. Логические высказывания.
Карта Карно — таблица, построенная так, что в ее соседние клетки попадают смежные наборы переменных функций — наборы, отличающиеся значением одной переменной (в один набор эта переменная входит в прямой форме, а в другой — в обратной). Карты Карно были предложены в 1952 г. Эдвардом В. Вейчем (американским ученым в области кибернетики) и усовершенствованы в 1953 г. Морисом Карно, чтобы упростить проектирование цифровых систем.
Морис Карно — американский физик Пример 26.2. Способы задания логической функции. 1. Функция двух переменных принимает значение 1, если эти переменные равны 1, а во всех других случаях функция равна 0. 2.
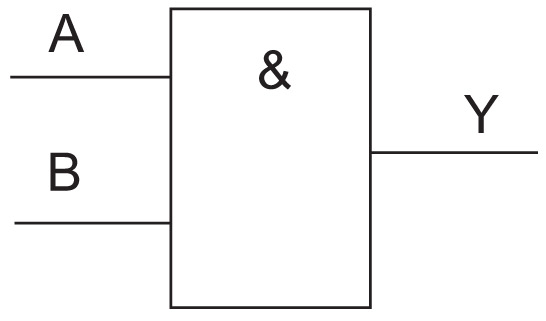
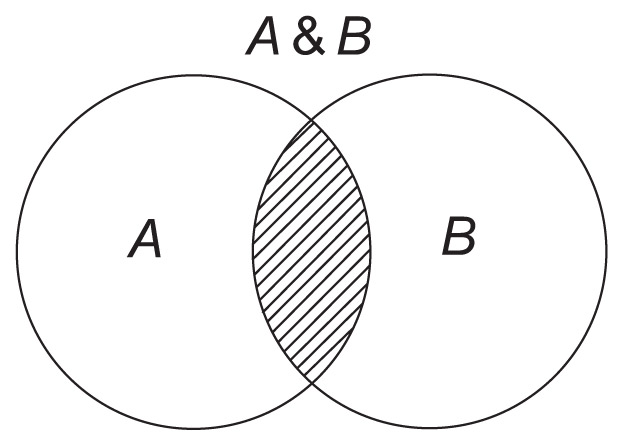
3. Y = A & B 4. 5.
6.
Анализ логических устройств — это поиск аналитического выражения, которое описывает работу системы.
Синтез логических устройств — обратная задача: создание технического устройства на основе математического описания средствами алгебры логики. В компьютерных устройствах применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае ток проходит, во втором — нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах. |