§ 26. Алгебра логики
| Сайт: | Профильное обучение |
| Курс: | Информатика. 10 класс (Повышенный уровень) |
| Книга: | § 26. Алгебра логики |
| Напечатано:: | Гость |
| Дата: | Sunday, 23 November 2025, 08:44 |
26.1. Логические высказывания
|
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. Для того чтобы иметь представление об устройстве компьютера, необходимо познакомиться не только с арифметическими, но и с основными логическими элементами, лежащими в основе его построения. Для понимания принципа работы таких элементов рассмотрим основные понятия алгебры логики. Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях. Аналогию между алгеброй и логикой положил в основу своего логического учения основоположник алгебры логики английский математик и логик Дж. Буль (1815–1864). Любое высказывание Буль записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов. Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно — 1 или ложно — 0. Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения. Истинность или ложность высказываний зависит от истинности и ложности исходных (простых) высказываний и смысла логических операций над высказываниями (пример 26.1). Таким образом, определение истинности некоторого логического выражения — это определение значения некоторой логической функции. Логическая функция — функция, принимающая значения 0 или 1 в результате логических операций над логическими переменными. Способы задания логической функции: 1) словесное описание; 2) таблица истинности; 3) формула, записанная с помощью букв, знаков логических операций и скобок; 4) комбинационная схема, составленная из логических элементов; 5) координатный способ (карта Карно); 6) диаграмма Венна (Эйлера). Области применения алгебры логики: 1) в качестве средства алгоритмического описания в языках программирования для определения логических условий; 2) для формирования логических высказываний в математической логике, лингвистике, теории искусственного интеллекта; 3) в разработке и описании дискретных технических систем; 4) при анализе и синтезе логических устройств. |
Пример 26.1. Логические высказывания.
Карта Карно — таблица, построенная так, что в ее соседние клетки попадают смежные наборы переменных функций — наборы, отличающиеся значением одной переменной (в один набор эта переменная входит в прямой форме, а в другой — в обратной). Карты Карно были предложены в 1952 г. Эдвардом В. Вейчем (американским ученым в области кибернетики) и усовершенствованы в 1953 г. Морисом Карно, чтобы упростить проектирование цифровых систем.
Морис Карно — американский физик Пример 26.2. Способы задания логической функции. 1. Функция двух переменных принимает значение 1, если эти переменные равны 1, а во всех других случаях функция равна 0. 2.
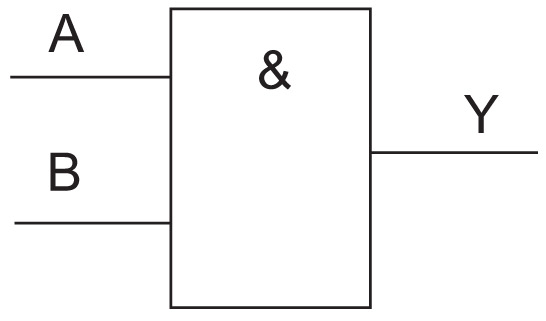
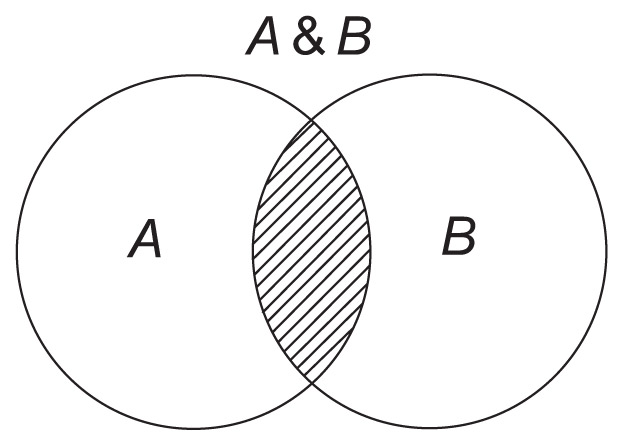
3. Y = A & B 4. 5.
6.
Анализ логических устройств — это поиск аналитического выражения, которое описывает работу системы.
Синтез логических устройств — обратная задача: создание технического устройства на основе математического описания средствами алгебры логики. В компьютерных устройствах применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае ток проходит, во втором — нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах. |
26.2. Логические операции
|
Рассмотрим основные логические операции — варианты обозначения (пример 26.3), таблицы истинности и логические элементы для каждой из логических операций (примеры 26.4 — 26.9). Логическое отрицание, или инверсия (лат. inversion — переворачивание), — логическая операция, которая меняет значение исходного высказывания на противоположное. Инверсия — унарная логическая операция, т. к. выполняется относительно одного высказывания (пример 26.4). Логические операции, которые выполняются относительно как минимум двух высказываний, называются бинарными. Рассмотрим основные из них. Логическое умножение, или конъюнкция (лат. conjunctio — соединение), — операция, соединяющая два или более высказываний при помощи логической связки ИЛИ. Результат операции может быть истинным только в том случае, если одновременно истинны исходные высказывания (пример 26.5). Логическое сложение, или дизъюнкция (лат. disjunction — разделение), — операция, соединяющая два или более высказываний при помощи логической связки ИЛИ. Результат операции будет истинным, если истинно хотя бы одно из исходных высказываний (пример 26.6). Дизъюнкция строгая (сложение по модулю два) — операция, соединяющая два высказывания ( А и В) при помощи логической связки ИЛИ, употребленной в исключающем смысле, и читается: «либо , либо ». Результат операции будет истинным, если истинно только одно из исходных высказываний (пример 26.7). Логическое следование, или импликация (лат. implisito — тесно связываю), — операция, соединяющая два высказывания (А и В), из которых первое является условием, а второе — следствием из этого условия. Читается: «Если А, то В», «А влечет В», «Из А следует В». Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь (пример 26.8). Равнозначность, или эквивалентность (лат. aequalis — равный и valentis — имеющий силу), — операция, позволяющая из двух высказываний (А и В) получить высказывание, которое читается так: «А равнозначно В». Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Операция эквивалентности противоположна строгой дизъюнкции и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают (пример 26.9). |
Пример 26.3. Варианты обозначений логических операций.
Пример 26.4. Инверсия.
Пример 26.5. Конъюнкция.
Пример 26.6. Дизъюнкция.
Пример 26.7. Дизъюнкция строгая.
«Этот треугольник тупоугольный или остроугольный» — высказывание истинно, если выполняется какое-то одно из условий. Пример 26.8. Импликация.
«Если 2 ∙ 2 = 4, то вода — это газ». Высказывание ложно, так как 2 ∙ 2 = 4 (предпосылка истинна), а вода не является газом (следствие ложно). Пример 26.9. Эквивалентность. |
26.3. Логические выражения и законы логики
|
Логическое выражение (формула) — содержит логические переменные, обозначающие высказывания, соединенные знаками логических операций. С помощью логических переменных и логических операций любое составное логическое высказывание можно формализовать, т. е. заменить логическим выражением. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу (пример 26.10). Смысл высказываний не учитывается, рассматривается только их истинность или ложность. В логических выражениях должен соблюдаться следующий порядок выполнения операций (пример 26.11): 1) действия в скобках; 2) инверсия; 3) конъюнкция; 4) дизъюнкция; 5) импликация; 6) эквивалентность. Значение логического выражения можно определить, построив таблицу истинности для этого выражения. Для построения таблицы истинности необходимо выполнить следующие действия (пример 26.12): 1) подсчитать число переменных в выражении (n); 2) подсчитать число логических операций в выражении (p); 3) установить последовательность выполнения логических операций в выражении с учетом скобок и приоритетов; 4) вычислить количество столбцов в таблице (n + p); 5) заполнить шапку таблицы, включив в нее переменные и операции в соответствии с установленной в п. 3 последовательностью; 6) вычислить количество строк в таблице (m = 2n); 7) записать в таблице все возможные наборы значений переменных; 8) заполнить таблицу по столбцам, выполняя логические операции в соответствии с установленной в п. 3 последовательностью. Для преобразования и упрощения формул в алгебре логики производятся эквивалентные преобразования, опирающиеся на основные логические законы (пример 26.13). Некоторые из этих законов формулируются и записываются так же, как аналогичные законы в арифметике и алгебре, другие выглядят непривычно. Доказано, что для представления любой логической функции достаточно трех операций: конъюнкции, дизъюнкции и отрицания. То есть любую логическую формулу можно путем преобразований и упрощений привести к формуле, содержащей только эти три основные логические операции. Пример 26.14. Упростить логическое выражение Выполним эквивалентные преобразования выражения в соответствии с законами логики:
|
Пример 26.10. Формализация высказываний. Высказывание «Если три меньше шести (A), то суббота всегда наступает после пятницы (B)» соответствует формуле A Высказывание «Если я куплю яблоки (A) или абрикосы (B), то приготовлю фруктовый пирог (C)» можно записать в виде формулы A V B Пример 26.11. Порядок выполнения действий в логических выражениях. Выражение: Порядок действий: 1) 2) 3) 4) 5) Пример 26.12. Построение таблицы истинности для выражения 1) n = 3; 2) p = 3; 3) дизъюнкция (V), инверсия ( 4) n + p = 6; 5)
6) m = 23 = 8; 3) - 8)
Пример 26.13. Основные законы алгебры логики. 
Преобразование выражения: 1) 2) 3) 4) Логическая схема: В арифметико-логических устройствах (АЛУ) процессора суммирование двоичных разрядов выполняют сумматоры — сложные устройства, состоящие из более простых элементов — вентилей. Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание. |
Вопросы к параграфу
 |
1. Что изучает алгебра логики? 2. Какими объектами оперирует алгебра логики? 3. Какие значения могут принимать объекты алгебры логики? 4. Какими способами можно отразить логическую функцию? 5. Какая логическая операция является унарной? Почему? В чем ее смысл? 6. В каком случае результатом конъюнкции будет истина? 7. В каком случае результатом дизъюнкции будет ложь? 8. В чем разница между дизъюнкцией и строгой дизъюнкцией? 9. Как выполняется импликация? Приведите примеры. 10. В каких случаях результатом эквивалентности будет истина? Приведите примеры. 11. В виде каких логических элементов реализованы логические операции: инверсия, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквивалентность? 12. Что такое логическое выражение? В чем состоит формализация составного логического высказывания? 13. По каким правилам строится таблица истинности для логического выражения? 14. Для чего в алгебре логики используются эквивалентные преобразования логических формул? 15. Какие законы используются при эквивалентных преобразованиях логических формул? 16. Каких логических операций достаточно для представления любой логической функции? |
Упражнения



1. Каким логическим операциям соответствуют следующие высказывания?
- В жаркий день приятно выпить стакан холодной воды или лимонада.
- Кто не работает, тот не ест.
- При записи чисел в двоичной системе счисления используются цифры 0 и 1.
- Если число кратно 4, то оно кратно 2.
2. Формализуйте следующий вывод: «Если A и B истинны, то C — истинно. Но C — ложно, значит, A или B ложны».
2.1 Определите результат логической функции при заданных значениях переменных:
3. Какое значение будет на выходе логической схемы?

4. По заданной логической формуле постройте логическую схему и определите значение логической функции при заданных A, B и C.
5. Какая формула соответствует логической схеме?

6. Даны простые высказывания:
A = «Процессор — устройство для обработки информации».
B = «Сканер — устройство вывода информации».
C = «Монитор — устройство ввода информации».
D = «Клавиатура — устройство вывода информации».
Определите истинность логических формул:
7. Постройте таблицы истинности для следующих логических выражений:
8. Определите для указанных значений X значение логической функции
- X = 1.
- X = 12.
- X = 3.
9. Для каких приведенных слов ложно логическое выражение «¬(первая буква гласная & третья буква гласная) строка из 4 символов»?
- Асса.
- Силач.
- Кукуруза.
- Куку.
- Ошибка.
10. Определите такое наименьшее натуральное число А, что выражение
принимает значение «истина» при любом натуральном значении Х.