§ 5. Ураўненне стану ідэальнага газу: Ураўненне стану ідэальнага газу

§ 5. Ураўненне стану ідэальнага газу

Высветлім, як звязаны паміж сабой макраскапічныя параметры ідэальнага газу, якія характарызуюць яго раўнаважны стан: ціск, маса ўсяго газу, адведзены яму аб’ём і тэмпература.

Стан макраскапічнай сістэмы цалкам вызначаны, калі вядомыя яе макраскапічныя параметры — ціск p, маса m, тэмпература T і аб’ём V. Ураўненне, якое звязвае параметры дадзенага стану, называюць ураўненнем стану сістэмы. Змяненне параметраў стану сістэмы з цягам часу называюць працэсам.

Калі пры пераходзе ідэальнага газу з аднаго стану ў другі колькасць яго малекул $N space equals space m over M N subscript straight A$ застаецца пастаяннай, гэта значыць маса і малярная маса газу не змяняюцца, то з ураўненняў $p space equals space n k T$ і $n space equals space N over V$ вынікае:

$p subscript 1 V subscript 1 space equals space N k T subscript 1$ , $p subscript 2 V subscript 2 space equals space N k T subscript 2$ ,

(5.1)

дзе k — пастаянная Больцмана; p₁, V₁, T₁ — параметры пачатковага стану газу, а p₂, V₂, T₂ — канчатковага. З суадносін (5.1) вынікае, што

$fraction numerator p subscript 1 V subscript 1 over denominator T subscript 1 end fraction space equals space fraction numerator p subscript 2 V subscript 2 over denominator T subscript 2 end fraction$

або

$fraction numerator p V over denominator T end fraction space equals space const$

(5.2)

Пры нязменных масе і малярнай масе ідэальнага газу адносіны здабытку яго ціску і аб’ёму да абсалютнай тэмпературы з’яўляюцца велічынёй пастаяннай.

Ураўненне (5.2) звязвае два станы ідэальнага газу незалежна ад таго, якім чынам газ перайшоў з аднаго стану ў другі.

Ураўненне стану ў выглядзе (5.2) упершыню вывеў у 1834 г. французскі фізік Бенуа Клапейрон (1799–1864), таму яго называюць ураўненнем Клапейрона.

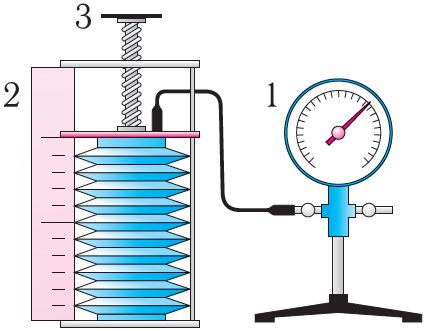
У праўдзівасці ўраўнення стану можна пераканацца, выкарыстаўшы прыладу, паказаную на малюнку 18. Манометрам 1, які злучаны з герметычнай гафрыраванай пасудзінай, рэгіструюць ціск газу ўнутры пасудзіны. Аб’ём газу ў пасудзіне можна разлічыць з дапамогай лінейкі 2. Тэмпература газу ў пасудзіне роўная тэмпературы навакольнага асяроддзя, і яе можа вымераць тэрмометрам.

Вызначыўшы параметры газу p₁, V₁, T₁ у пачатковым стане, вылічваюць адносіны $fraction numerator p subscript 1 V subscript 1 over denominator T subscript 1 end fraction$ . Пасля гэтага змяшчаюць пасудзіну ў гарачую ваду, тым самым змяняючы тэмпературу газу і яго ціск. Верцячы вінт 3, змяняюць умяшчальнасць пасудзіны. Вымераўшы зноў ціск газу p₂ і тэмпературу T₂, а таксама разлічыўшы адведзены яму аб’ём V₂, вылічваюць адносіны $fraction numerator p subscript 2 V subscript 2 over denominator T subscript 2 end fraction$ . Як паказваюць разлікі, ураўненне стану (5.2) выконваецца ў межах хібнасці эксперымента.

Ураўненне стану (5.2) можна прымяняць для газаў пры наступных умовах:

1) не вельмі значныя ціскі (пакуль уласны аб’ём усіх малекул газу надзвычай малы ў параўнанні з умяшчальнасцю ёмістасці, у якой знаходзіцца газ);

2) не вельмі нізкія або высокія тэмпературы (пакуль абсалютнае значэнне патэнцыяльнай энергіі міжмалекулярнага ўзаемадзеяння надзвычай малое ў параўнанні з кінетычнай энергіяй цеплавога руху малекул).

Ад тэорыі да практыкі

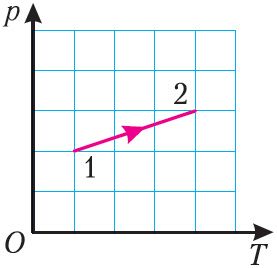
На малюнку 19 прыведзены графік працэсу пераходу ідэальнага газу дадзенай масы са стану 1 у стан 2. Як змяніўся аб’ём газу ў выніку гэтага працэсу?

Паколькі колькасць часціц $N space equals space m over M N subscript straight A$ , то з ураўнення (5.1) вынікае:

$p V space equals space k N subscript straight A m over M T$

(5.3)

Велічыню, роўную здабытку пастаяннай Больцмана k і пастаяннай Авагадра N_A, назвалі ўніверсальнай газавай пастаяннай R:

$R space equals space k N subscript straight A space equals space 1 comma 38 times 10 to the power of negative 23 end exponent space Дж over straight К times 6 comma 02 times 10 to the power of 23 space 1 over моль space equals space 8 comma 31 space fraction numerator Дж over denominator моль times straight К end fraction$

(5.4)

З улікам выразу (5.4) ураўненне (5.3) прыме выгляд:

$p V space equals space m over M R T.$

(5.5)

Паколькі колькасць рэчыва $v space equals space m over M$ , то формулу (5.5) можна запісаць у выглядзе:

pV = νRT.

Ураўненне стану ў выглядзе (5.5) упершыню было атрыманае рускім вучоным Д. І. Мендзялеевым (1834–1907) у 1874 г., таму яго называюць ураўненнем Клапейрона — Мендзялеева.

Адзначым, што ўраўненне Клапейрона — Мендзялеева звязвае паміж сабой макраскапічныя параметры канкрэтнага стану ідэальнага газу. Выкарыстоўваючы ўраўненне Клапейрона — Мендзялеева, можна апісаць розныя працэсы, якія адбываюцца ў ідэальным газе.