§ 5. Ураўненне стану ідэальнага газу
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 10 клас |
| Книга: | § 5. Ураўненне стану ідэальнага газу |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 6 Июль 2025, 08:40 |
Высветлім, як звязаны паміж сабой макраскапічныя параметры ідэальнага газу, якія характарызуюць яго раўнаважны стан: ціск, маса ўсяго газу, адведзены яму аб’ём і тэмпература.
Стан макраскапічнай сістэмы цалкам вызначаны, калі вядомыя яе макраскапічныя параметры — ціск p, маса m, тэмпература T і аб’ём V. Ураўненне, якое звязвае параметры дадзенага стану, называюць ураўненнем стану сістэмы. Змяненне параметраў стану сістэмы з цягам часу называюць працэсам.
Калі пры пераходзе ідэальнага газу з аднаго стану ў другі колькасць яго малекул застаецца пастаяннай, гэта значыць маса і малярная маса газу не змяняюцца, то з ураўненняў
і
вынікае:
,
,
(5.1)
дзе k — пастаянная Больцмана; p1, V1, T1 — параметры пачатковага стану газу, а p2, V2, T2 — канчатковага. З суадносін (5.1) вынікае, што
або
(5.2)
Пры нязменных масе і малярнай масе ідэальнага газу адносіны здабытку яго ціску і аб’ёму да абсалютнай тэмпературы з’яўляюцца велічынёй пастаяннай.
Ураўненне (5.2) звязвае два станы ідэальнага газу незалежна ад таго, якім чынам газ перайшоў з аднаго стану ў другі.
Ураўненне стану ў выглядзе (5.2) упершыню вывеў у 1834 г. французскі фізік Бенуа Клапейрон (1799–1864), таму яго называюць ураўненнем Клапейрона.
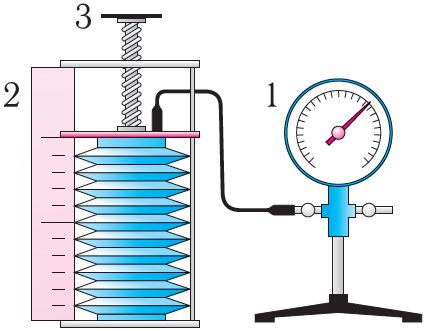
У праўдзівасці ўраўнення стану можна пераканацца, выкарыстаўшы прыладу, паказаную на малюнку 18. Манометрам 1, які злучаны з герметычнай гафрыраванай пасудзінай, рэгіструюць ціск газу ўнутры пасудзіны. Аб’ём газу ў пасудзіне можна разлічыць з дапамогай лінейкі 2. Тэмпература газу ў пасудзіне роўная тэмпературы навакольнага асяроддзя, і яе можа вымераць тэрмометрам.
Вызначыўшы параметры газу p1, V1, T1 у пачатковым стане, вылічваюць адносіны . Пасля гэтага змяшчаюць пасудзіну ў гарачую ваду, тым самым змяняючы тэмпературу газу і яго ціск. Верцячы вінт 3, змяняюць умяшчальнасць пасудзіны. Вымераўшы зноў ціск газу p2 і тэмпературу T2, а таксама разлічыўшы адведзены яму аб’ём V2, вылічваюць адносіны
. Як паказваюць разлікі, ураўненне стану (5.2) выконваецца ў межах хібнасці эксперымента.
Ураўненне стану (5.2) можна прымяняць для газаў пры наступных умовах:
1) не вельмі значныя ціскі (пакуль уласны аб’ём усіх малекул газу надзвычай малы ў параўнанні з умяшчальнасцю ёмістасці, у якой знаходзіцца газ);
2) не вельмі нізкія або высокія тэмпературы (пакуль абсалютнае значэнне патэнцыяльнай энергіі міжмалекулярнага ўзаемадзеяння надзвычай малое ў параўнанні з кінетычнай энергіяй цеплавога руху малекул).
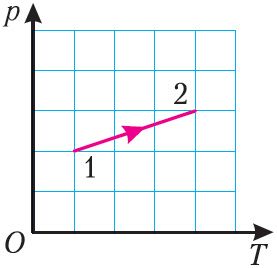
На малюнку 19 прыведзены графік працэсу пераходу ідэальнага газу дадзенай масы са стану 1 у стан 2. Як змяніўся аб’ём газу ў выніку гэтага працэсу?
Паколькі колькасць часціц , то з ураўнення (5.1) вынікае:
(5.3)
Велічыню, роўную здабытку пастаяннай Больцмана k і пастаяннай Авагадра NA, назвалі ўніверсальнай газавай пастаяннай R:
(5.4)
З улікам выразу (5.4) ураўненне (5.3) прыме выгляд:
(5.5)
Паколькі колькасць рэчыва , то формулу (5.5) можна запісаць у выглядзе:
pV = νRT.
Ураўненне стану ў выглядзе (5.5) упершыню было атрыманае рускім вучоным Д. І. Мендзялеевым (1834–1907) у 1874 г., таму яго называюць ураўненнем Клапейрона — Мендзялеева.
Адзначым, што ўраўненне Клапейрона — Мендзялеева звязвае паміж сабой макраскапічныя параметры канкрэтнага стану ідэальнага газу. Выкарыстоўваючы ўраўненне Клапейрона — Мендзялеева, можна апісаць розныя працэсы, якія адбываюцца ў ідэальным газе.
![]()
Ціск сумесі газаў. У паўсядзённым жыцці часта даводзіцца мець справу не з газам, якія складаюцца з аднолькавых малекул, а з сумессю некалькіх разнастайных газаў, не якія ўступалі ў хімічныя рэакцыі пры разгляданых умовах. Напрыклад, паветра ў пакоі з'яўляецца сумессю азоту (78,08 %), кіслароду (20,95 %), інертных газаў і вадароду (0,94 %), вуглякіслага газу (0,03 %) і ў невялікіх колькасцях азону, аксіду вугляроду(II), аміяку, метану, аксіду серы(IV), а таксама некаторых іншых газаў (хімічны састаў паветра прыведзены ў аб'ёмных долях*).
З прычыны цеплавога руху часціц кожнага газу, што ўваходзіць у састаў газавай сумесі, яны раўнамерна размяркоўваюцца па ўсім аб’ёме, які займае сумесь. Сутыкненні часціц забяспечваюць у сумесі цеплавую раўнавагу.
Кожны газ уносіць свой уклад у сумарны ціск газавай сумесі, ствараючы ціск, які называюць парцыяльным.
Парцыяльны ціск — ціск газу, які ўваходзіць у састаў газавай сумесі, калі б ён адзін займаў увесь аб’ём, адведзены сумесі, пры той жа тэмпературы.
Сумесь ідэальных газаў лічаць ідэальным газам.
![]()
Закон Дальтана. Разгледзім сумесь хімічна не рэагуючых разрэджаных газаў, якія знаходзяцца ў пасудзіне ўмяшчальнасцю V. Дакажам, што ціск кожнага газу, які ўваходзіць у састаў сумесі, не залежыць ад наяўнасці астатніх разрэджаных газаў і рэзультуючы ціск вызначаецца сумарным ціскам усіх кампанентаў газавай сумесі.
Агульная колькасць часціц газаў у пасудзіне: , дзе
— колькасць часціц кожнага газу.
Абазначым праз парцыяльныя ціскі кожнага газу. Тады, улічваючы суадносіны
, атрымаем:
адкуль
(5.6)
Формула (5.6) з'яўляецца матэматычным выразам закона, эксперыментальна ўстаноўленага Дальтанам і названага законам Дальтана: ціск сумесі хімічна не рэагуючых паміж сабой газаў роўны суме парцыяльных ціскаў усіх газаў, якія ўтвараюць сумесь.
З гісторыі фізікі
Фундаментальныя даследаванні газавых сумесей правёў англійскі вучоны Джон Дальтан (1766–1844). Iм быў сфармуляваны закон незалежнасці парцыяльнага ціску кампанентаў сумесі (1801–1802). У 1802 г. на некалькі месяцаў раней французскага вучонага Жозэфа Гей-Люсака(1778–1850) Дальтан вынайшоў закон цеплавога расшырэння газаў, а таксама ўвёў паняцце атамнай вагі.

![]()
1. Што называюць ураўненнем стану ідэальнага газу?
2. Як звязаны параметры ідэальнага газу ва ўраўненні стану?
3. Які ціск называюць парцыяльным?
![]()
4. Сфармулюйце закон Дальтана.
5. Якое паветра цяжэйшае — сухое або вільготнае (пры аднолькавых тэмпературы і ціску)?
* Аб’ёмная доля — працэнтныя суадносіны змешчаных у адзінцы аб’ёму сумесі часціц (атамаў або малекул) газу, які ўваходзіць у састаў сумесі, да агульнай колькасці часціц ў адзінцы аб’ёму сумесі. ↑
Прыклад 1. Балон з газам, ціск якога p1 = 2,84 МПа, знаходзіўся ў неацепленым памяшканні, дзе тэмпература паветра t1 = 7 °С. Пасля таго як некаторая колькасць газу была зрасходавана, балон унеслі ў памяшканне, дзе тэмпература паветра t2 = 27 °С. Вызначце, якая частка газу была зрасходавана, калі пасля працяглага знаходжання балона ў ацепленым памяшканні ціск газу ў ім стаў p2 = 1,52 МПа.
p1 = 2,84 МПа = 2,84 · 106 Па
T1 = 280 К, T2 = 300 К
p2 = 1,52 МПа = 1,52 · 106 Па
Рашэнне. Калі не прымаць пад увагу цеплавое расшырэнне балона, то яго ёмістасць не змяняецца. Запішам ураўненне Клапейрона — Мендзялеева для пачатковага і канчатковага станаў газу, палічыўшы яго ідэальным:
,
,
адкуль
,
.
Тады
.
.
Адказ: .
![]()
Прыклад 2. Вызначце шчыльнасць газавай сумесі, якая складаецца з вадароду масай m1 = 8,0 г і кіслароду масай m2 = 40 г, калі ціск і тэмпература сумесі р = 1,27 · 105 Па і t = 7 °С адпаведна.
m1 = 8,0 г = 8,0 · 10−3 кг
m2 = 40 г = 4,0 · 10−2 кг
p = 1,27 · 105 Па
Т = 280 К
Рашэнне. Шчыльнасць газавай сумесі
(1)
дзе m = m1 + m2 — маса сумесі, V — аб'ём сумесі. Паколькі вадарод і кісларод пры нізкіх тэмпературах хімічна не рэагуюць, то можна выкарыстаць закон Дальтана: р = р1 + р2, дзе р1 i р2 — парцыяльныя ціскі вадароду і кіслароду адпаведна.
Іх можна вызначыць, выкарыстаўшы ўраўненне Клапейрона — Мендзялеева:
i
,
дзе i
— малярныя масы вадароду і кіслароду адпаведна. Тады ціск сумесі
, а яе аб’ём
.
Падставіўшы значэнні масы m сумесі і яе аб’ёму V у формулу (1), атрымаем:
Адказ: .
Практыкаванне 4
1. Вызначце колькасць рэчыва ідэальнага газу, які знаходзіцца ў пасудзіне ёмістасцю V = 480 см3 пры нармальных умовах (атмасферны ціск р0 = 1,0 · 105 Па, тэмпература t0 = 0,0 °С).
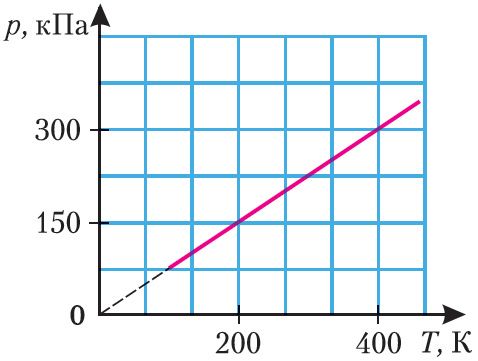
2. На малюнку 20 прыведзены графік залеж насці ціску вадароду, маса якога m = 100 г, ад абсалютнай тэмпературы. Вызначце аб’ём, які займае газ.
3. Балон ёмістасцю V1 = 15 л, дзе знаходзіцца газ, ціск якога p1 = 2,0 · 106 Па, злучылі з пустым балонам ёмістасцю V2 = 5,0 л. Вызначце ціск газу, які ўстанавіўся ў балонах, калі тэмпература пасля расшырэння газу праз некаторы прамежак часу стала такой, як і да расшырэння.
4. Азот, аб’ём якога V1 = 2,9 м3, тэмпература Т1 = 293 К і ціск p1 = 2,0 · 105 Па, перавялі ў вадкі стан. Вызначце аб’ём, які зай мае вадкі азот, калі яго шчыльнасць ρ = 0,86 .
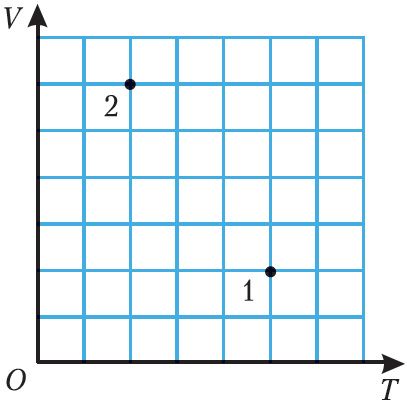
5. На малюнку 21 пункты 1 і 2 адпавядаюць розным станам ідэальнага газу пэўнай масы. Вызначце, у колькі разоў адрозніваюцца ціскі газу ў станах 1 і 2.
![]()
6. У пасудзіне ўмяшчальнасцю V = 2,0 л знаходзяцца кісларод масай m1 = 4,0 г і азот масай m2 = 7,0 г. Вызначце ціск сумесі газаў, калі яе абсалютная тэмпература Т = 300 К.
7. У балоне ўмяшчальнасцю V = 12 л знаходзіўся ідэальны газ, першапачатковыя ціск і тэмпература якога p1 = 1,2 · 105 Па і t1 = 27 °С. Пасля таго як з балона выпусцілі частку газу, у ім устанавілася тэмпература t2 = 17 °С. Вызначце ціск газу, што застаўся ў балоне, калі колькасць рэчыва выпушчанага газу ν1 – ν2 = 0,10 моль.
8. Вакууміраваная цыліндрычная пасудзіна ўмяшчальнасцю V = 2 л падзелена на дзве роўныя часткі тонкай перагародкай, якая прапускае толькі малекулы вадароду. У адну з частак пасудзіны ўпусцілі вадарод Н2 і азот N2, масы якіх m1 = 4 г і m2 = 14 г адпаведна. Вызначце ціск сумесі газаў, калі пры дасягненні цеплавой раўнавагі абсалютная тэмпература сістэмы склала Т = 320 К.