§ 33. З’ява самаіндукцыі. Індуктыўнасць. Энергія магнітнага поля шпулі з токам
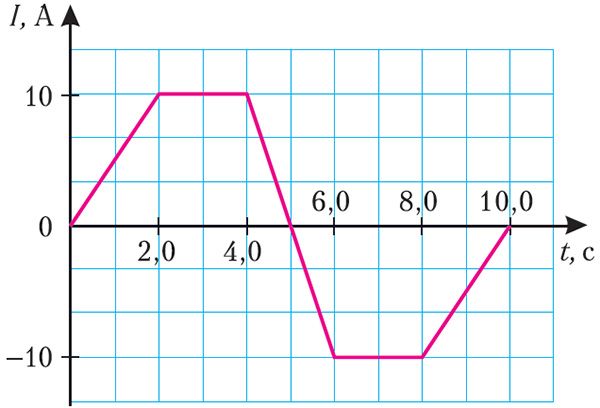
Прыклад 1. На малюнку 186 прыведзены графік залежнасці сілы току, які праходзіць па саленоідзе, ад часу. Вызначце максімальнае значэнне модуля ЭРС самаіндукцыі ў саленоідзе, калі яго індуктыўнасць L = 40 мГн.
L = 40 мГн = 4,0 · 10–2 Гн
Рашэнне. ЭРС самаіндукцыі . Аналізуючы графік (мал. 186), можна зрабіць вы снову, што сіла току, які праходзіць па са леноідзе, змяняецца на трох участках:
1) ад моманту часу t1 = 0,0 с да моманту часу t2 = 2,0 с сіла току змяняецца на ΔI1 = 10 А за прамежак часу Δt1 = 2,0 с;
2) ад моманту часу t3 = 4,0 с да моманту часу t4 = 6,0 с сіла току змяняецца на ΔI2 = –20 А за прамежак часу Δt2 = 2,0 с;
3) ад моманту часу t5 = 8,0 с да моманту часу t6 = 10,0 с сіла току змяняецца на ΔI3 = 10 А за прамежак часу Δt3 = 2,0 с.
Паколькі прамежкі часу Δt1 = Δt2 = Δt3 = 2,0 с, то відавочна, што максімальнае значэнне модуля скорасці змянення сілы току, а значыць, і максімальнае значэнне модуля ЭРС самаіндукцыі, створанай у саленоідзе, адпавядае прамежку часу Δt2 = 2,0 с (ад t3 = 4,0 с да t4 = 6,0 с):
Такім чынам,
Адказ: = 0,40 В.
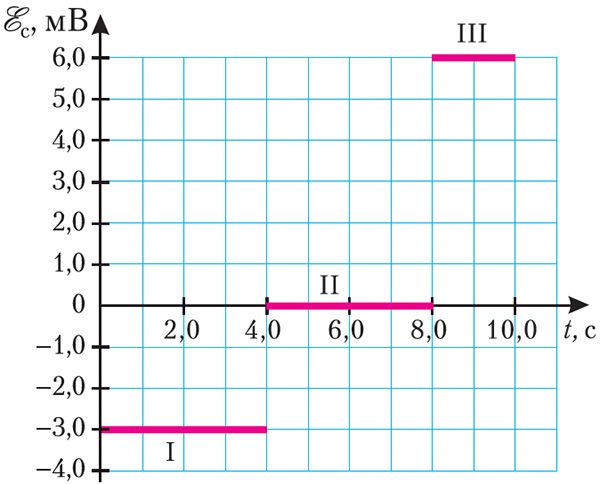
Прыклад 2. На малюнку 187 прыведзены графік залежнасці ЭРС самаіндукцыі, якая ўзнікае ў шпулі з індуктыўнасцю L = 2,0 мГн, ад часу. Вызначце змяненне сілы току на ўчастках I, II і III графіка. Чаму роўная энергія магнітнага поля ў момант часу t = 4,0 с, калі ў пачатковы момант часу сіла току ў шпулі I = 0?
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔIIII — ? Wм — ?
Рашэнне. Аналізуючы графік, можна зрабіць выснову, што на ўчастку I ЭРС самаіндукцыі = –3,0 мВ, на ўчастку III —
= 6,0 мВ. Змену сілы току на гэтых участках графіка можна вызначыць, выкарыстаўшы закон электрамагнітнай індукцыі для з’явы самаіндукцыі:
;
.
;
.
На ўчастку II графіка = 0, значыць, сіла току не змянялася: ΔIII = 0.
У момант часу t = 4,0 с энергія магнітнага поля шпулі .
Такім чынам,
.
Адказ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
![]()
Прыклад 3. За прамежак часу Δt = 9,50 мс сіла току ў шпулі індукцыўнасці раўнамерна ўзрасла ад I1 = 1,60 А да I2 = 2,40 А. Пры гэтым у шпулі ўзнікла ЭРС самаіндукцыі 1с = –14,0 В. Вызначце ўласны магнітны паток у канцы працэсу нарастання току і прырашчэнне энергіі магнітнага поля шпулі.
Δt = 9,50 мс = 9,50 · 10–3 с
I1 = 1,60 А
I2 = 2,40 А
ΔWм — ?
Рашэнне. Пры змяненні на шпулі сілы току ад I1 да I2 ўзнікае ўласны магнітны паток Фс = LI2. Індукцыўнасць шпулі L можна вызначыць з закона электрамагнітнай індукцыі для з'явы самаіндукцыі: . Значыць,
. Тады
.
Прырашчэнне энергіі магнітнага поля шпулі
Адказ: Фс = 399 мВб, ΔWм = 266 мДж.