§ 33. З’ява самаіндукцыі. Індуктыўнасць. Энергія магнітнага поля шпулі з токам

Сайт:	Профильное обучение
Курс:	Фізіка. 10 клас
Книга:	§ 33. З’ява самаіндукцыі. Індуктыўнасць. Энергія магнітнага поля шпулі з токам
Напечатано::	Гость
Дата:	Воскресенье, 6 Июль 2025, 08:27

Фарадэй доследным шляхам вызначыў, што электрамагнітная індукцыя праяўляецца ва ўсіх выпадках змянення магнітнага патоку праз паверхню, абмежаваную контурам. Сучаснік Фарадэя амерыканскі фізік Джозэф Генры (1797–1878) незалежна ад свайго англійскага калегі адкрыў некаторыя з электрамагнітных эфектаў. У 1829 г. Генры выявіў, што ЭРС індукцыі ўзнікае ў нерухомым контуры і пры адсутнасці змянення знешняга магнітнага поля. Які механізм узнікнення ЭРС індукцыі ў гэтым выпадку?

Самаіндукцыя. Калі электрычны ток, які праходзіць у замкнутым праводным контуры, па якіх-небудзь прычынах змяняецца, то змяняецца і магнітнае поле, створанае гэтым токам. Гэта цягне за сабой змяненне магнітнага патоку праз паверхню, абмежаваную контурам. Паколькі магнітны паток Ф прапарцыянальны модулю магнітнай індукцыі В поля, які, у сваю чаргу, прапарцыянальны сіле току I ў контуры, то

$straight Ф tilde I.$

Каэфіцыенту прапарцыянальнасці паміж магнітным патокам Ф і сілай току I Томсан (лорд Кельвін) у 1853 г. прапанаваў даць назву «каэфіцыент самаіндукцыі»:

Ф = LI.

(33.1)

Каэфіцыент самаіндукцыі L часта называюць індуктыўнасцю контуру. У СІ індуктыўнасць вымяраюць у генры (Гн). Індуктыўнасць контуру роўная 1 Гн, калі пры сіле току ў контуры 1 А магнітны паток праз паверхню, абмежаваную гэтым контурам, роўны 1 Вб. Індуктыўнасць залежыць ад памераў і формы контуру, а таксама ад магнітных уласцівасцей асяроддзя, у якім знаходзіцца гэты контур.

Калі электрычны ток, які праходзіць у контуры, змяняецца, то ён стварае зменлівы магнітны паток, што прыводзіць да з’яўлення ЭРС індукцыі. Гэтую з’яву назвалі самаіндукцыяй.

Самаіндукцыя — з’ява ўзнікнення ЭРС індукцыі ў электрычным ланцугу ў выніку змены сілы току ў гэтым ланцугу.

ЭРС, якая ўзнікае ў гэтым выпадку, назвалі электрарухаючай сілай самаіндукцыі. Згодна з законам электрамагнітнай індукцыі

$calligraphic E subscript straight с equals negative fraction numerator increment straight Ф over denominator increment t end fraction equals negative fraction numerator increment open parentheses L I close parentheses over denominator increment t end fraction.$

Калі індуктыўнасць контуру не змяняецца з цягам часу, гэта значыць L = const, то

$calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction.$

Паколькі контур замкнуты, ЭРС самаіндукцыі стварае ў ім ток самаіндукцыі. Сілу току самаіндукцыі можна вызначыць паводле закона Ома $I subscript straight с equals calligraphic E subscript straight с over R$ , дзе R — супраціўленне контуру. Паводле правіла Ленца ток самаіндукцыі заўсёды накіраваны так, каб супрацьдзейнічаць змене току, створанага крыніцай. Пры ўзрастанні сілы току ток самаіндукцыі накіраваны супраць току крыніцы, а пры памяншэнні — напрамкі току крыніцы і току самаіндукцыі супадаюць.

Ад тэорыі да практыкі

Якой павінна быць скорасць змянення сілы току, каб у шпулі з індук тыўнасцю L = 0,20 Гн узнікла ЭРС самаіндукцыі $calligraphic E subscript straight с$ = 4,0 В?

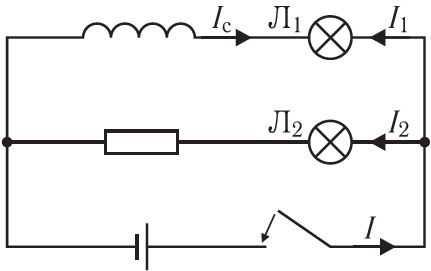
Назіранне самаіндукцыі. Для назірання з’явы самаіндукцыі збяром электрычны ланцуг, які складаецца са шпулі з вялікай індуктыўнасцю, рэзістара з электрычным супраціўленнем, роўным супраціўленню абмоткі шпулі, дзвюх аднолькавых лямпачак, ключа і крыніцы пастаяннага току. Схема ланцуга прыведзена на малюнку 185. Пры замыканні ключа лямпачка Л₂ пачынае свяціцца практычна адразу, а лямпачка Л₁ — з прыкметным спазненнем. Пры ўзрастанні сілы току I₁, створанага крыніцай на ўчастку, утвораным шпуляй і лямпачкай Л₁, ЭРС самаіндукцыі ў шпулі мае такую палярнасць, што створаны ёю ток самаіндукцыі I_с накіраваны насустрач току крыніцы. У выніку рост сілы току I₁ крыніцы запавольваецца, і сіла току I = I₁ – |I_с| не адразу дасягае свайго максімальнага значэння.

Адсылка да электроннага дадатку для павышанага ўзроўню

З'яву самаіндукцыі можна назіраць і пры размыканні электрычнага ланцуга. Збяром ланцуг, які складаецца са шпулі з вялікай колькасцю віткоў 1, наматаных на жалезны асяродак 2, да заціскаў якой подключана лямпачка з вялікім электрычным супраціўленнем у параўнанні з супраціўленнем абмоткі шпулі (мал. 185.1). У якасці крыніцы току возьмем крыніцу, ЭРС якой 2 В. Лямпачка падключана паралельна шпулі. Пры размыканні ключа захоўваецца замкнутай частка ланцуга, якая складаецца з ужо паслядоўна злучаных шпулі і лямпачкі.

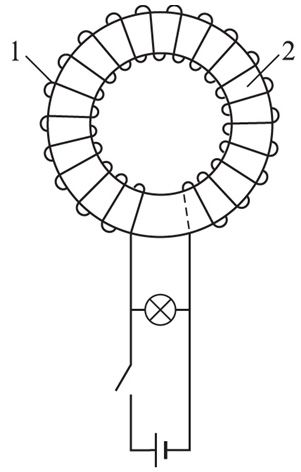
Пакуль ключ замкнуты, лямпачка будзе цьмяна свяціцца, бо адносіны сіл токаў, што праходзяць праз лямпачку і шпулю, адваротныя адносінам іх супраціўленняў $I subscript straight л over I subscript straight к equals R subscript straight к over R subscript straight л$ . Калі ўключыць лямпачку паралельна шпулі ў электрычны ланцуг пастаяннага току, то пры размыканні ланцуга можна ўбачыць, што лямпачка ярка ўспыхвае. Чаму гэта адбываецца? Пры размыканні ланцуга сіла току ў шпулі памяншаецца, што прыводзіць да ўзнікнення ЭРС самаіндукцыі. Ток самаіндукцыі, які ўзнікае ў ланцугу, паводле правіла Ленца, супадае па напрамку з токам шпулі, не дазваляючы яму рэзка змяншаць сілу току. Гэта і забяспечвае ўспышку лямпачкі. Заўважым, што з’ява самаіндукцыі мае месца ў любых выпадках змянення сілы току ў ланцугу, які змяшчае індуктыўнасць, або змянення самой індуктыўнасці.

Энергія магнітнага поля. Адкуль бярэцца энергія, якая забяспечвае ўспышку лямпачкі? Гэта не энергія крыніцы току, бо яна ўжо адключана. Успышка лямпачкі адбываецца адначасова з памяншэннем сілы току ў шпулі і створанага токам магнітнага поля. Можна меркаваць, што назапашаная ў шпулі ў працэсе самаіндукцыі энергія магнітнага поля ператвараецца ва ўнутраную энергію спіралі лямпачкі і энергію яе выпраменьвання.

Адсылка да электроннага дадатку для павышанага ўзроўню

Пры замыканні ланцуга, што складаецца з крыніцы току з ЭРС $calligraphic E subscript 0$ , шпулі з індуктыўнасцю L і рэзістара, супраціўленне якога R, сіла току ў ланцугу пачне ўзрастаць і з'явіцца ЭРС самаіндукцыі $calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction$ .

Тады ў адпаведнасці з законам Ома сіла току ў ланцугу $I equals fraction numerator calligraphic E subscript 0 plus calligraphic E subscript straight с over denominator R end fraction$ .

Значыць, $calligraphic E subscript 0 equals I R plus L fraction numerator increment I over denominator increment t end fraction$ .

Памножыўшы атрыманую роўнасць на IΔt, дзе Δt — дастаткова малы прамежак часу, на працягу якога сіла току I застаецца практычна пастаяннай, знойдзем элементарную работу, выкананую пабочнымі сіламі ў крыніцы току: $calligraphic E subscript 0 I increment t equals I squared R increment t plus L I increment I$ .

У працэсе ўстанаўлення току, калі сіла току I і магнітны паток Ф = LI узрастаюць, работа, якую выконваюць пабочныя сілы ў крыніцы току, перавышае колькасць цеплаты, што выдзяляецца ў рэзістары. Элементарная дадатковая работа, выкананая пабочнымі сіламі за прамежак часу Δt пры пераадоленні ЭРС самаіндукцыі ў працэсе ўстанаўлення току (мал. 185.2):

δA_дад = ФΔI.

Поўная дадатковыя работа А_дад, роўная суме элементарных дадатковых работ δА_дад у працэсе ўстанаўлення току, роўная суме плошчаў усіх аналагічных слупкоў, гэта значыць плошчы фігуры пад графікам залежнасці Ф = Ф(I) (гл. мал. 185.2 ).

$A subscript дад equals fraction numerator straight Ф subscript уст I subscript уст over denominator 2 end fraction equals fraction numerator L I subscript уст superscript 2 over denominator 2 end fraction.$

Гэтая работа ператвараецца ў энергію магнітнага поля шпулі, таму:

$W subscript straight м equals fraction numerator L I squared over denominator 2 end fraction comma$

дзе L — індуктыўнасць контуру; I — сіла току.

Ад тэорыі да практыкі

Якая індуктыўнасць шпулі, калі пры сіле току I = 2,0 А энергія магнітнага поля шпулі W_м = 1,2 Дж?

1. Што называюць самаіндукцыяй?

2. У якіх доследах можна назіраць з’яву самаіндукцыі?

3. Ад чаго залежыць ЭРС самаіндукцыі?

4. Што называюць індуктыўнасцю? У якіх адзінках у СІ яе вымяраюць?

5. Як вылічыць энергію магнітнага поля шпулі з токам?

Адсылка да электроннага дадатку для павышанага ўзроўню

6. Чаму для стварэння электрычнага току ў ланцугу са шпуляй індуктыўнасці крыніца току павінна затраціць энергію?

Прыклады рашэння задач

Прыклад 1. На малюнку 186 прыведзены графік залежнасці сілы току, які праходзіць па саленоідзе, ад часу. Вызначце максімальнае значэнне модуля ЭРС самаіндукцыі ў саленоідзе, калі яго індуктыўнасць L = 40 мГн.

Дадзена:
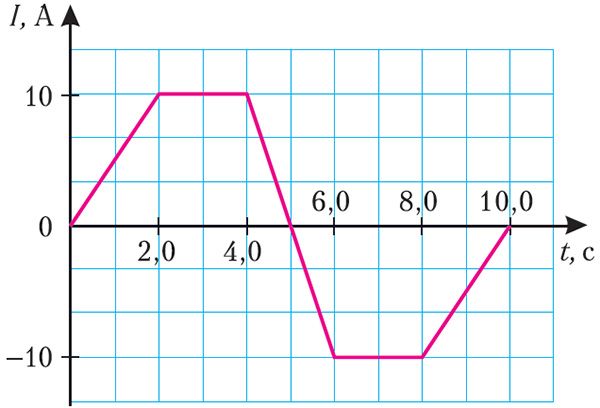
L = 40 мГн = 4,0 · 10^–2 Гн

open vertical bar calligraphic E subscript straight с close vertical bar subscript max

— ?

Рашэнне. ЭРС самаіндукцыі $calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction$ . Аналізуючы графік (мал. 186), можна зрабіць вы снову, што сіла току, які праходзіць па са леноідзе, змяняецца на трох участках:

1) ад моманту часу t₁ = 0,0 с да моманту часу t₂ = 2,0 с сіла току змяняецца на ΔI₁ = 10 А за прамежак часу Δt₁ = 2,0 с;

2) ад моманту часу t₃ = 4,0 с да моманту часу t₄ = 6,0 с сіла току змяняецца на ΔI₂ = –20 А за прамежак часу Δt₂ = 2,0 с;

3) ад моманту часу t₅ = 8,0 с да моманту часу t₆ = 10,0 с сіла току змяняецца на ΔI₃ = 10 А за прамежак часу Δt₃ = 2,0 с.

Паколькі прамежкі часу Δt₁ = Δt₂ = Δt₃ = 2,0 с, то відавочна, што максімальнае значэнне модуля скорасці змянення сілы току, а значыць, і максімальнае значэнне модуля ЭРС самаіндукцыі, створанай у саленоідзе, адпавядае прамежку часу Δt₂ = 2,0 с (ад t₃ = 4,0 с да t₄ = 6,0 с):

Такім чынам,

$open vertical bar calligraphic E subscript straight с close vertical bar subscript max equals 4 comma 0 times 10 to the power of negative 2 end exponent space Гн times fraction numerator open vertical bar negative 20 space straight А close vertical bar over denominator 2 comma 0 space straight с end fraction equals 0 comma 40 space straight В.$

Адказ: $open vertical bar calligraphic E subscript straight с close vertical bar subscript max$ = 0,40 В.

Прыклад 2. На малюнку 187 прыведзены графік залежнасці ЭРС самаіндукцыі, якая ўзнікае ў шпулі з індуктыўнасцю L = 2,0 мГн, ад часу. Вызначце змяненне сілы току на ўчастках I, II і III графіка. Чаму роўная энергія магнітнага поля ў момант часу t = 4,0 с, калі ў пачатковы момант часу сіла току ў шпулі I = 0?

Дадзена:
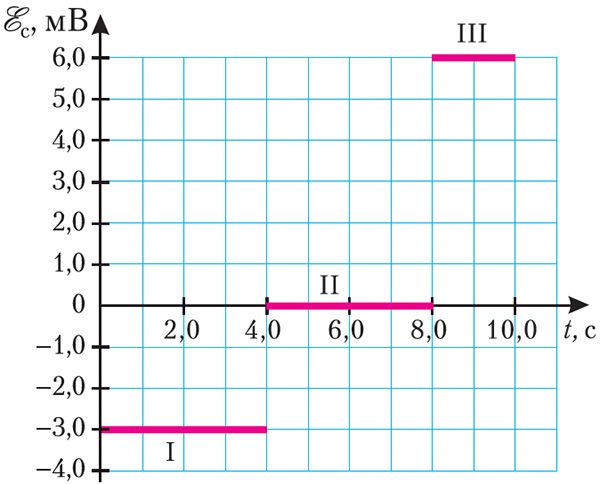
L = 2,0 мГн = 2,0 · 10^–3 Гн
t = 4,0 с

ΔI_I — ? ΔI_II — ?
ΔI_III — ? W_м — ?

Рашэнне. Аналізуючы графік, можна зрабіць выснову, што на ўчастку I ЭРС самаіндукцыі $calligraphic E subscript сI$ = –3,0 мВ, на ўчастку III — $calligraphic E subscript сIII$ = 6,0 мВ. Змену сілы току на гэтых участках графіка можна вызначыць, выкарыстаўшы закон электрамагнітнай індукцыі для з’явы самаіндукцыі:

$calligraphic E subscript с equals negative L fraction numerator increment I over denominator increment t end fraction$ ; $increment I equals negative fraction numerator calligraphic E subscript с increment t over denominator L end fraction$ .

$increment I subscript straight I equals negative fraction numerator negative 3 comma 0 times 10 to the power of negative 3 end exponent space straight В times 4 comma 0 space straight с over denominator 2 comma 0 times 10 to the power of negative 3 end exponent space Гн end fraction equals 6 comma 0 space straight А$ ; $increment I subscript III equals negative fraction numerator 6 comma 0 times 10 to the power of negative 3 end exponent space straight В times 2 comma 0 space straight с over denominator 2 comma 0 times 10 to the power of negative 3 end exponent space Гн end fraction equals negative 6 comma 0 space straight А$ .

На ўчастку II графіка $calligraphic E subscript с II end subscript$ = 0, значыць, сіла току не змянялася: ΔI_II = 0.

У момант часу t = 4,0 с энергія магнітнага поля шпулі $W subscript straight м equals fraction numerator L I squared over denominator 2 end fraction$ .

Такім чынам,

$W subscript straight м equals fraction numerator 2 comma 0 times 10 to the power of negative 3 end exponent space Гн times open parentheses 6 comma 0 space straight А close parentheses squared over denominator 2 end fraction equals 36 times 10 to the power of negative 3 end exponent space Дж equals 36 space мДж$ .

Адказ: ΔI_I = 6,0 А; ΔI_II = 0; ΔI_III = –6,0 А; W_м = 36 мДж.

Адсылка да электроннага дадатку для павышанага ўзроўню

Прыклад 3. За прамежак часу Δt = 9,50 мс сіла току ў шпулі індукцыўнасці раўнамерна ўзрасла ад I₁= 1,60 А да I₂= 2,40 А. Пры гэтым у шпулі ўзнікла ЭРС самаіндукцыі 1_с= –14,0 В. Вызначце ўласны магнітны паток у канцы працэсу нарастання току і прырашчэнне энергіі магнітнага поля шпулі.

Дадзена:
Δt = 9,50 мс = 9,50 · 10^–3 с
I1 = 1,60 А
I2 = 2,40 А

calligraphic E subscript straight с

= ‒14,0 В

Фс — ?
ΔWм — ?

Рашэнне. Пры змяненні на шпулі сілы току ад I₁да I₂ўзнікае ўласны магнітны паток Ф_с= LI₂. Індукцыўнасць шпулі L можна вызначыць з закона электрамагнітнай індукцыі для з'явы самаіндукцыі: $calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction equals negative L fraction numerator I subscript 2 minus I subscript 1 over denominator increment t end fraction$ . Значыць,

$L equals negative fraction numerator calligraphic E subscript straight с increment t over denominator I subscript 2 minus I subscript 1 end fraction equals fraction numerator calligraphic E subscript straight с increment t over denominator I subscript 1 minus I subscript 2 end fraction$ . Тады $straight Ф subscript straight с equals fraction numerator calligraphic E subscript straight с increment t I subscript 2 over denominator I subscript 1 minus I subscript 2 end fraction$ .

$straight Ф subscript straight с equals fraction numerator negative 14 comma 0 space straight В times 9 comma 50 times 10 to the power of negative 3 end exponent space straight с times 2 comma 40 space straight А over denominator 1 comma 60 space straight А minus 2 comma 40 space straight А end fraction equals 0 comma 399 space Вб equals 399 space мВб.$

Прырашчэнне энергіі магнітнага поля шпулі

$increment W subscript straight м equals W subscript straight м 2 end subscript minus W subscript straight м 1 end subscript equals fraction numerator L I subscript 2 superscript 2 over denominator 2 end fraction minus fraction numerator L I subscript 1 superscript 2 over denominator 2 end fraction equals L over 2 open parentheses I subscript 2 superscript 2 minus I subscript 1 superscript 2 close parentheses equals fraction numerator negative calligraphic E subscript straight с increment t open parentheses I subscript 2 superscript 2 minus I subscript 1 superscript 2 close parentheses over denominator 2 open parentheses I subscript 2 minus I subscript 1 close parentheses end fraction equals fraction numerator negative calligraphic E subscript straight с increment t open parentheses I subscript 2 plus I subscript 1 close parentheses over denominator 2 end fraction.$

$increment W subscript straight м equals fraction numerator negative open parentheses negative 14 comma 0 space straight В close parentheses times 9 comma 50 times 10 to the power of negative 3 end exponent space straight с times left parenthesis 2 comma 40 space straight А plus 1 comma 60 straight А right parenthesis over denominator 2 end fraction equals 0 comma 266 space Дж space equals space 266 space мДж.$

Адказ: Фс = 399 мВб, ΔWм = 266 мДж.

Практыкаванне 24

1. Сіла току, які праходзіць па замкнутым праводным контуры, I = 1,2 А. Магнітнае поле гэтага току стварае магнітны паток Ф = 3,0 мВб праз паверхню, абмежаваную контурам. Вызначце індуктыўнасць контуру.

2. Пры раўнамерным змяненні сілы току ў шпулі на ΔI = –4,0 А за прамежак часу Δt = 0,10 с у ёй узнікае ЭРС самаіндукцыі $calligraphic E subscript straight с$ = 20 В. Вызначце індуктыўнасць шпулі.

3. Вызначце ЭРС самаіндукцыі, якая ўзнікае ў шпулі, індуктыўнасць якой L = 1,2 Гн, пры раўнамерным змяненні сілы току ад I₁ = 2,0 А да I₂ = 6,0 А за прамежак часу Δt = 0,60 с. Вызначце прырашчэнне энергіі магнітнага поля пры дадзенай змене сілы току.

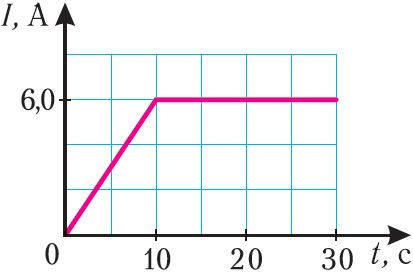
4. На малюнку 188 прыведзены графік залежнасці сілы току ў шпулі, індуктыўнасць якой L = 10 мГн, ад часу. Вызначце ЭРС самаіндукцыі праз прамежкі часу t₁ = 10 с і t₂ = 20 с ад моманту пачатку адліку часу.

5. Сіла току ў шпулі раўнамерна паменшылася ад I₁ = 10 А да I₂ = 5,0 А. Пры гэтым энергія магнітнага поля змянілася на ΔW_м = –3,0 Дж. Вызначце індуктыўнасць шпулі і першапачатковае значэнне энергіі магнітнага поля.

6. Вызначце ЭРС самаіндукцыі, што ўзнікае ў шпулі, індуктыўнасць якой L = 0,12 Гн, пры раўнамерным памяншэнні сілы току ад I₁ = 8,0 А, калі за прамежак часу t₁ = 0,20 с энергія магнітнага поля паменшылася ў α = 2,0 раза.

Адсылка да электроннага дадатку для павышанага ўзроўню

7. Энергія магнітнага поля шпулі з індуктыўнасцю L₁= 0,5 Гн большая за энергію магнітнага поля шпулі з індуктыўнасцю L₂у α = 1,5 раза. Вызначце індуктыўнасць другой шпулі, калі адносіны ўласнага магнітнага патоку праз паверхні, абмежаваныя віткамі другой шпулі, да ўласнага магнітнага патоку праз паверхні, абмежаваныя віткамі першай шпулі, $straight Ф subscript 2 over straight Ф subscript 1 equals 2$ .

§ 33. З’ява самаіндукцыі. Індуктыўнасць. Энергія магнітнага поля шпулі з токам

Оглавление