§ 21. Работа сілы аднароднага электрастатычнага поля. Патэнцыял
![]()
Патэнцыяльная энергія зараду ў электрастатычным полі. Выкарыстаўшы закон захавання энергіі, можна паказаць, што любое электрастатычнае поле з'яўляецца патэнцыяльным. Гэта азначае, што электрастатычнае і гравітацыйнае палі маюць падобныя ўласцівасці, якія вызначаюцца іх патэнцыяльным характарам. У дачыненні да электрастатычнага полі гэтыя ўласцівасці праяўляюцца ў наступным:
а) пунктавы электрычны зарад, які знаходзіцца ў любым пункце электрастатычнага поля, валодае патэнцыяльнай энергіяй узаемадзеяння з гэтым полем. Значэнне гэтай энергіі вызначаюць адносна адвольна выбранага нулявога пункта. У нулявым пункце патэнцыяльную энергію зараду прымаюць роўнай нулю. Патэнцыяльная энергія ўзаемадзеяння пунктавага зараду з электрастатычным полем роўная рабоце, якую выканала б сіла поля пры перамяшчэнні дадзенага зараду з пэўнага пункта поля ў нулявы пункт;
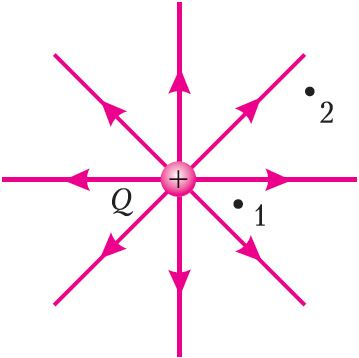
б) работа сілы поля па перамяшчэнні электрычнага зараду q з пункта 1 у пункт 2 (мал. 116) можа служыць мерай змены патэнцыяльнай энергіі гэтага зараду ў полі, створаным зарадам Q.
Няхай Wп1 і Wп2 — патэнцыяльныя энергіі перамешчанага зараду ў пунктах 1 і 2 электрастатычнага поля. Тады работа сілы поля
A12 = –ΔWп12 = –(Wп2 – Wп1),
(21.2)
дзе ΔWп12 — прырашчэнне патэнцыяльнай энергіі зараду q пры яго перамяшчэнні з пункта 1 у пункт 2.
Перапішам выраз (21.2) у выглядзе
A12 = Wп1 – Wп2
(21.3)
і прааналізуем яго для выпадку, калі на зарад q дзейнічае толькі сіла з боку электрастатычнага поля:
1) калі работа сілы поля A12 > 0 (перамяшчэнне дадатнага зараду q адбываецца ў напрамку ліній напружанасці поля), то патэнцыяльная энергія зараду памяншаецца: ΔWп12 < 0. Пры гэтым згодна з законам захавання энергіі павялічваецца кінетычная энергія цела c зарадам q: ;
2) калі работа сілы поля A12 < 0 (перамяшчэнне дадатнага зараду адбываецца супрацьлегла напрамку ліній напружанасці поля), то патэнцыяльная энергія зараду павялічваецца: ΔWп12 > 0. Пры гэтым кінетычная энергія зараджанага цела змяншаецца: ;
3) калі работа сілы поля A12 = 0 (перамяшчэнне зараду адбываецца перпендыкулярна напрамку ліній напружанасці поля), то патэнцыяльная энергія зараду не змяняецца.
![]()
Трэба падкрэсліць, што патэнцыяльная энергія — гэта энергія ўзаемадзеяння, і яе неабходна адносіць не да зараджанай часціцы або цела, а да сістэмы ў цэлым. У прыватнасці, для зараджанай часціцы (цела), якая знаходзіцца ў электрастатычным полі, гэта патэнцыяльная энергія ўзаемадзеяння зараджанай часціцы з полем, дакладней — з іншымі зараджанымі часціцамі і (або) целамі, якія з'яўляюцца крыніцамі гэтага поля. Коратка гэта прынята фармуляваць так: патэнцыяльная энергія зараду ў полі.
У якім выпадку (гл. мал. 115) пры перамяшчэнні дадатнага (адмоўнага) зараду паміж двума пунктамі поля патэнцыяльная энергія гэтага зараду: а) павялічваецца; б) памяншаецца; в) не змяняецца?