§ 21. Работа сілы аднароднага электрастатычнага поля. Патэнцыял
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 10 клас |
| Книга: | § 21. Работа сілы аднароднага электрастатычнага поля. Патэнцыял |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 6 Июль 2025, 08:50 |
Электрастатычнае поле, дзейнічаючы на змешчаныя ў ім зарады з пэўнай сілай, можа іх перамяшчаць. Вы ведаеце, што пры перамяшчэнні цела дзеючая на яго сіла выконвае работу. Высветлім, ад чаго залежыць работа сілы па перамяшчэнні электрычнага зараду ў электрастатычным полі.
Работа сілы аднароднага электрастатычнага поля. Разлікі і вынікі эксперыментаў даказалі, што работа сілы электрастатычнага поля пры перамяшчэнні зараду паміж двума пунктамі залежыць толькі ад становішча гэтых пунктаў і не залежыць ад формы траекторыі. Такой самай асаблівасцю, як вы ведаеце, валодае і гравітацыйнае поле. Фізічныя палі, работа сіл якіх не залежыць ад формы траекторыі, называюць патэнцыяльнымі.
Пакажам, што электрастатычнае поле патэнцыяльнае.
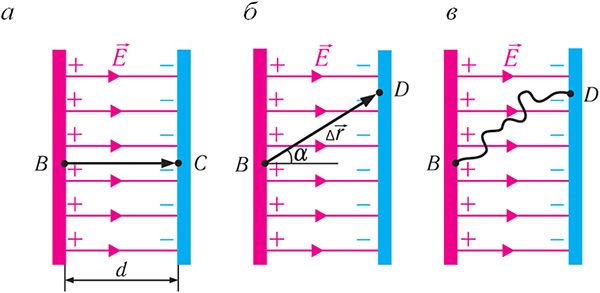
Няхай дадатны пробны зарад q0 перамяшчаюць у аднародным электрастатычным полі напружанасцю з пункта В у пункт С уздоўж лініі напружанасці дадзенага поля (мал. 114, а). Пры гэтым сіла, якой поле дзейнічае на зарад q, выконвае работу. У скалярным выглядзе выраз для работы мае выгляд A = FΔrcosα, дзе α — вугал паміж напрамкамі сілы
і перамяшчэння Δ
зараду. Модуль электрычнай сілы F = q0E, cosα = 1 (напрамкі сілы і перамяшчэння зараду супадаюць), а Δr = d, дзе d — адлегласць паміж пунктамі В і С. Тады работа сілы аднароднага электрастатычнага поля па перамяшчэнні зараду:
AВD = q0Ed.
(21.1)
![]()
Калі зарад перамяшчаюць па прамой з пункта В у пункт D пад вуглом α да напрамку напружанасці поля (мал. 114, б), то Δrcosα = d. Работа сілы поля па перамяшчэнні зараду і ў гэтым выпадку:
ABD= FΔrcosα = q0Ed.
Відавочна, што для перамяшчэння зараду ў адваротным напрамку (з пункта D у пункт В) знешняй сіле патрабуецца, пераадольваючы сілу поля, выканаць работу, мінімальнае значэнне якой будзе такім жа: = ABD, таму ABD = ‒ADB. Такім чынам, калі зарад вяртаецца ў пачатковы пункт, гэта значыць пры руху зараду па замкнутай траекторыі, работа сілы поля роўная нулю.
Дапусцім, што перамяшчэнне зараду q0 з пункта В у пункт D адбываецца ў аднародным электрастатычным полі напружанасцю па крывалінейнай траекторыі (мал. 114, в). У гэтым выпадку траекторыю можна разбіць на такія малыя ўчасткі, каб кожны з іх можна было лічыць прамалінейным. Калі падсумаваць работы сілы на кожным з гэтых участкаў, то атрымаем:
AВD = q0E(Δd1 + Δd2 + … Δdі + + Δdn) = q0Ed,
дзе Δdі = Δrіcosαі, Δrі — модуль перамяшчэння на i-м малым участку траекторыі, αi — вугал паміж напрамкамі перамяшчэння Δ і напружанасці
поля (i = 1, 2, 3, ..., n ).
Такім чынам, работа сілы аднароднага электрастатычнага поля па перамяшчэнні зараду з аднаго пункта поля ў другі не залежыць ад формы траекторыі, гэта значыць аднароднае электрастатычнае поле патэнцыяльнае.
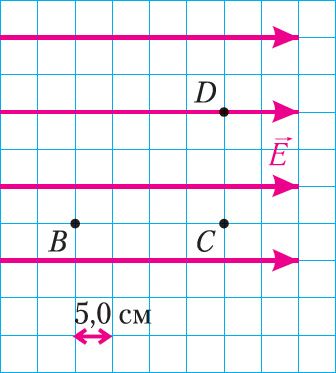
Якую работу выканае сіла аднароднага электрастатычнага поля, модуль напружанасці якога , пры перамяшчэнні зараду q = 2,4 нКл па адрэзку прамой (мал. 115), што злучае пункты: а) В і С; б) С і D; в) D і В?
Якую работу выканае сіла поля пры перамяшчэнні зараду па замкнутай траекторыі BCDB?
![]()
Патэнцыяльная энергія зараду ў электрастатычным полі. Выкарыстаўшы закон захавання энергіі, можна паказаць, што любое электрастатычнае поле з'яўляецца патэнцыяльным. Гэта азначае, што электрастатычнае і гравітацыйнае палі маюць падобныя ўласцівасці, якія вызначаюцца іх патэнцыяльным характарам. У дачыненні да электрастатычнага полі гэтыя ўласцівасці праяўляюцца ў наступным:
а) пунктавы электрычны зарад, які знаходзіцца ў любым пункце электрастатычнага поля, валодае патэнцыяльнай энергіяй узаемадзеяння з гэтым полем. Значэнне гэтай энергіі вызначаюць адносна адвольна выбранага нулявога пункта. У нулявым пункце патэнцыяльную энергію зараду прымаюць роўнай нулю. Патэнцыяльная энергія ўзаемадзеяння пунктавага зараду з электрастатычным полем роўная рабоце, якую выканала б сіла поля пры перамяшчэнні дадзенага зараду з пэўнага пункта поля ў нулявы пункт;
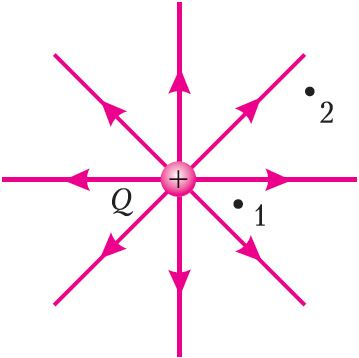
б) работа сілы поля па перамяшчэнні электрычнага зараду q з пункта 1 у пункт 2 (мал. 116) можа служыць мерай змены патэнцыяльнай энергіі гэтага зараду ў полі, створаным зарадам Q.
Няхай Wп1 і Wп2 — патэнцыяльныя энергіі перамешчанага зараду ў пунктах 1 і 2 электрастатычнага поля. Тады работа сілы поля
A12 = –ΔWп12 = –(Wп2 – Wп1),
(21.2)
дзе ΔWп12 — прырашчэнне патэнцыяльнай энергіі зараду q пры яго перамяшчэнні з пункта 1 у пункт 2.
Перапішам выраз (21.2) у выглядзе
A12 = Wп1 – Wп2
(21.3)
і прааналізуем яго для выпадку, калі на зарад q дзейнічае толькі сіла з боку электрастатычнага поля:
1) калі работа сілы поля A12 > 0 (перамяшчэнне дадатнага зараду q адбываецца ў напрамку ліній напружанасці поля), то патэнцыяльная энергія зараду памяншаецца: ΔWп12 < 0. Пры гэтым згодна з законам захавання энергіі павялічваецца кінетычная энергія цела c зарадам q: ;
2) калі работа сілы поля A12 < 0 (перамяшчэнне дадатнага зараду адбываецца супрацьлегла напрамку ліній напружанасці поля), то патэнцыяльная энергія зараду павялічваецца: ΔWп12 > 0. Пры гэтым кінетычная энергія зараджанага цела змяншаецца: ;
3) калі работа сілы поля A12 = 0 (перамяшчэнне зараду адбываецца перпендыкулярна напрамку ліній напружанасці поля), то патэнцыяльная энергія зараду не змяняецца.
![]()
Трэба падкрэсліць, што патэнцыяльная энергія — гэта энергія ўзаемадзеяння, і яе неабходна адносіць не да зараджанай часціцы або цела, а да сістэмы ў цэлым. У прыватнасці, для зараджанай часціцы (цела), якая знаходзіцца ў электрастатычным полі, гэта патэнцыяльная энергія ўзаемадзеяння зараджанай часціцы з полем, дакладней — з іншымі зараджанымі часціцамі і (або) целамі, якія з'яўляюцца крыніцамі гэтага поля. Коратка гэта прынята фармуляваць так: патэнцыяльная энергія зараду ў полі.
У якім выпадку (гл. мал. 115) пры перамяшчэнні дадатнага (адмоўнага) зараду паміж двума пунктамі поля патэнцыяльная энергія гэтага зараду: а) павялічваецца; б) памяншаецца; в) не змяняецца?
Патэнцыял электрастатычнага поля як яго энергетычная характарыстыка. З выразаў (21.1) і (21.2) вынікае, што патэнцыяльная энергія пробнага зараду q0 у дадзеным пункце поля прапарцыянальная велічыні гэтага зараду. Такім чынам, адносіны не залежаць ад зараду і з’яўляюцца энергетычнай характарыстыкай электрастатычнага поля, якая атрымала назву патэнцыял.
Патэнцыял электрастатычнага поля ў дадзеным пункце прасторы — фізічная скалярная велічыня, роўная адносінам патэнцыяльнай энергіі пробнага зараду, змешчанага ў дадзены пункт поля, да значэння гэтага зараду:
(21.4)
За адзінку патэнцыялу ў СІ прыняты вольт (В). Адзінка была названая ў гонар італьянскага вучонага Алясандра Вольта (1745–1827), які зрабіў важкі ўклад у вывучэнне электрычных з’яў. 1 В — патэнцыял такога пункта электрастатычнага поля, у якім зарад 1 Кл валодаў бы патэнцыяльнай энергіяй 1 Дж.
Патэнцыял φ электрастатычнага поля пунктавага зараду Q на адлегласці r ад яго ў вакууме або ў паветры вызначаюць суадносінамі
(21.5)
Знак заряду-крыніцы поля вызначае знак патэнцыялу гэтага поля.
Паколькі патэнцыяльная энергія зараду ў электрастатычным полі залежыць ад выбару нулявога пункта, то гэтая залежнасць захоўваецца і для патэнцыялу. Калі прыняць, што на бясконца вялікай адлегласці ад крыніцы поле адсутнічае, гэта значыць патэнцыяльная энергія сістэмы «зарад — электрастатычнае поле» на бясконцасці роўная нулю, то патэнцыял поля ў дадзеным пункце можна вызначыць наступным чынам:
.
Калі электрычнае поле створана ў аднародным асяроддзі з дыэлектрычнай пранікальнасцю ε, то патэнцыял поля
.
![]()
Варта адзначыць, што патэнцыял поля, стваранага дадатным зарадам, памяншаецца па меры аддалення ад зараду, а патэнцыял поля, створанага адмоўным зарадам, павялічваецца.
З формулы (21.5) вынікае, што ва ўсіх пунктах поля, якія знаходзяцца на адлегласці r ад пунктавага зараду Q, патэнцыял φ аднолькавы. Гэтыя пункты размешчаны на паверхні сферы радыусам R, цэнтр якой знаходзіцца ў тым жа пункце, што і зарад Q.
Патэнцыял поля, створанага раўнамерна зараджанай сферай радыусам R, зарад якой Q, у вакууме ў пунктах за сферай на адлегласці r > R ад яе цэнтра, вызначаюць па формуле У пунктах, якія знаходзяцца на паверхні і ўнутры сферы,
Электрастатычнае поле створана пунктавым нерухомым зарадам Q. Патэнцыял поля ў пункце, размешчаным ад зараду Q на адлегласці r = 27 см, φ = 80 В. У гэты пункт змяшчаюць пробны зарад q0. Вызначце: а) значэнне зараду, які стварае поле; б) значэнне пробнага зараду, калі яго патэнцыяльная энергія ў дадзеным пункце поля Wп = –0,8 мкДж.
![]()
Патэнцыял з'яўляецца скалярнай велічынёй. Таму, калі ў дадзеным пункце прасторы электрастатычнае поле створана сістэмай пунктавых зарадаў, то патэнцыял выніковага поля ў гэтым пункце роўны алгебраічнай суме патэнцыялаў палёў у гэтым жа пункце прасторы, якiя ствараюцца кожным з пунктавых зарадаў сістэмы паасобна :
φ = φ1 + φ2 + φ3 + … + φn,
т. е. для патэнцыялу выконваецца прынцып суперпазіцыі.
Геаметрычнае месца пунктаў у электрастатычным полі, патэнцыялы якіх аднолькавыя, называюць эквіпатэнцыяльнай паверхняй.
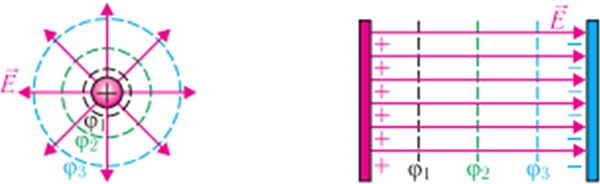
Выкарыстоўваючы эквіпатэнцыяльныя паверхні, можна адлюстроўваць графічна электрастатычныя палі. Праз кожны пункт поля праходзяць толькі адна лінія напружанасці і адна эквіпатэнцыяльная паверхня. У кожным пункце электрастатычнага поля лінія напружанасці і эквіпатэнцыяльная паверхня ўзаемна перпендыкулярныя (мал. 116.1). Адлюстраванне электрастатычнага поля з дапамогай эквіпатэнцыяльных паверхняў, як і тэрмін «патэнцыял», увёў нямецкі вучоны К. Ф. Гаўс у

![]()
1. Як можна вызначыць работу сілы аднароднага электрастатычнага поля па перамяшчэнні электрычнага зараду?
2. Як вы разумееце сцвярджэнне «электрастатычнае поле патэнцыяльнае»? Як звязана работа сілы электрастатычнага поля па перамяшчэнні электрычнага зараду са змяненнем патэнцыяльнай энергіі зараду ў гэтым полі?
3. Якія дзве фізічныя велічыні характарызуюць электрастатычнае поле ў любым яго пункце?
4. Што называюць патэнцыялам электрастатычнага поля?
5. Чаму роўны патэнцыял электрастатычнага поля пунктавага зараду Q на адлегласці r ад яго?
6. Як вызначаюць патэнцыял электрастатычнага поля, створанага некалькімі пунктавымі зарадамі?
![]()
7. Дакажыце, што работа сілы электрастатычнага поля па перамяшчэнні зараду па замкнутай траекторыі роўная нулю.
8. У чым праяўляецца падабенства электрастатычнага і гравітацыйнага палёў?
9. Дадатна зараджаная часціца перамяшчаецца пад дзеяннем толькі сіл электрастатычнага поля на некаторую адлегласць. У якім пункце траекторыі руху часціцы — пачатковым або канчатковым — патэнцыял поля вышэйшы, калі модуль яе скорасці: а) павялічваецца; б) памяншаецца?
10. Адмоўна зараджаная часціца перамяшчаецца са стану спакою пад дзеяннем толькі сіл электрастатычнага поля на некаторую адлегласць. У якім пункце траекторыі руху часціцы — пачатковым або канчатковым — патэнцыял поля вышэйшы?
11. Чаму роўны патэнцыял электрастатычнага поля раўнамерна зараджанай сферы радыусам R на адлегласці r ад яе цэнтра, калі: а) r ≤ R; б) r > R, а зарад сферы Q?
Прыклад 1. Электрастатычнае поле створана нерухомым пунктавым зарадам Q. У пункце, які знаходзіцца на адлегласці r = 80 см ад зараду, патэнцыял поля φ = 0,42 кВ. Вызначце модуль сілы, якая дзейнічае з боку поля на пунктавы зарад q = 1,5 нКл, змешчаны ў гэты пункт.
r = 80 см = 0,80 м
φ = 0,42 кВ = 4,2 · 102 В
q = 1,5 нКл = 1,5 · 10–9 Кл
Рашэнне. Модуль сілы, якой электрастатычнае поле зараду Q дзейнічае на зарад q2, можна вызначыць, выкарыстаўшы закон Кулона:
(1)
З формулы (21.5) для патэнцыялу поля пунктавага зараду знойдзем значэнне зараду:
(2)
Падставіўшы выраз (2) у формулу (1), атрымаем:
Адказ: F = 7,9 · 10–7 Н.
![]()
Прыклад 2. Электрон, рухаючыся са скорасцю, модуль якой = 4,0 · 105
, трапляе ў аднароднае электрастатычнае поле, напрамак ліній напружанасці якога супадае з напрамкам яго скорасці. Прайшоўшы адлегласць d =
d =
е = ‒1,6 · 10–19 Кл
mе = 9,1 · 10–Рашэнне. Да змены напрамку руху сіла аднароднага электрастатычнага поля выконвае адмоўную работу па тармажэнні электрона:
А = .
Гэтую работу таксама можна вызначыць па формуле А = eEd.
Значыць: = eEd. Тады E =
.
E=.
Згодна з законам захавання энергіі поўная энергія сістэмы «электрон — поле» застаецца нязменнай, гэта значыць ΔWп + ΔWк = 0. Такім чынам, ΔWп =, гэта значыць патэнцыяльная энергія электрона ўзрастае на велічыню
ΔWп = .
Адказ: E= , ΔWп
.
Прыклад 3. У цэнтры сферы з раўнамерна размеркаваным дадатным зарадам Q1 = 36 нКл знаходзіцца маленькі шарык з адмоўным зарадам, модуль якога |Q2| = 16 нКл. Вызначце патэнцыял электрастатычнага поля ў пункце, які знаходзіцца за сферай на адлегласці r =
Q 1 = 36 нКл = 3,6 · 10–8 Кл
Q 2 = ‒16 нКл = ‒1,6 · 10–8 Кл
r =Рашэнне. Патэнцыял у шукаемым пункце вызначым паводле прынцыпу суперпазіцыі: =
1 +
2, дзе
1 > 0 — патэнцыял электрастатычнага поля дадатна зараджанай сферы, а
2 < 0 — патэнцыял электрастатычнага поля адмоўна зараджанага шарыка. Паколькі
1 =
,
, то
.
.
Адказ: = 18В.
Практыкаванне 15
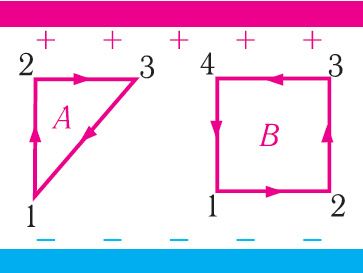
1. Ці залежыць работа сілы электрастатычнага поля ад траекторыі руху зараду? Параўнайце работу сілы электрастатычнага поля, утворанага зараджанымі пласцінамі, пры перамяшчэнні зараду q па контуры А і контуры В (мал. 117).
2. Адмоўны зарад, модуль якога |q| = 0,50 мкКл, перамясцілі ў аднародным электрастатычным полі на адлегласць d = 10 см у напрамку ліній напружанасці. Вызначце работу сілы поля, выкананую пры перамяшчэнні зараду, і змену патэнцыяльнай энергіі ўзаемадзеяння зараду з полем, калі модуль яго напружанасці .
3. Пунктавы зарад q = 5,0 нКл перамяшчаюць у аднародным электрастатычным полі, модуль напружанасці якога . Перамяшчэнне, модуль якога Δr = 8,0 см, утварае вугал α = 60° з напрамкамі ліній напружанасці поля. Вызначце работу сілы поля, змены патэнцыяльнай і кінетычнай энергій зараду, калі знешняя сіла забяспечвае толькі прамалінейнасць перамяшчэння зараду.
4. Работа, выкананая сілай электрастатычнага поля пры пераносе зараду q = 2,4 нКл з бясконцасці ў некаторы пункт поля, А = 72 нДж. Вызначце патэнцыял гэтага пункта поля. Што зменіцца, калі работу па пераносе першапачаткова нерухомага зараду выконвае знешняя сіла супраць сілы электрастатычнага поля? Мінімальнае значэнне работы знешняй сілы Азнешн = 72 нДж.
5. Модулі напружанасці двух пунктаў поля, стваранага нерухомым пунктавым зарадам, адрозніваюцца ў α = 9 разоў. Вызначце, у колькі разоў адрозніваюцца патэнцыялы гэтых пунктаў поля.
6. Электрастатычнае поле створана двума рознаіменнымі пунктавымі зарадамі, што знаходзяцца на адлегласці r = 80 см адзін ад аднаго, модулі якіх |Q1| = |Q2| = 6,4 нКл. Вызначце модуль напружанасці і патэнцыял у пункце прасторы, які знаходзіцца на сярэдзіне адрэзка, што злучае гэтыя зарады.
![]()
7. Адасобленая адмоўна зараджаная металічная сфера радыусам R =