§ 17. Узаемадзеянне пунктавых зарадаў. Закон Кулона

Прыклады рашэння задач

Прыклад 1. Два пунктавыя зарады знаходзяцца ў газе на адлегласці r1 = 42 см. Вызначце, на якой адлегласці павінны знаходзіцца гэтыя зарады ў гліцэрыне, каб модуль сіл іх электрастатычнага ўзаемадзеяння застаўся ранейшы. Дыэлектрычныя пранікальнасці газы ε1 = 2,0, гліцэрыны ε2 = 56,2.

Дадзена:
r1 = 42 см
Fк1 = Fк2
ε1 = 2,0
ε2 = 56,2
r2 — ?

Рашэнне. Паколькі Fк1 = Fк2, то, выкарыстаўшы закон Кулона, можна запісаць: k fraction numerator open vertical bar q subscript 1 close vertical bar times open vertical bar q subscript 2 close vertical bar over denominator straight epsilon subscript 1 r subscript 1 squared end fraction equals fraction numerator open vertical bar q subscript 1 close vertical bar times open vertical bar q subscript 2 close vertical bar over denominator straight epsilon subscript 2 r subscript 2 squared end fraction.

Значыць, r subscript 2 equals r subscript 1 square root of straight epsilon subscript 1 over straight epsilon subscript 2 end root.

r subscript 2 equals 42 space см space square root of fraction numerator 2 comma 0 over denominator 56 comma 2 end fraction end root equals 7 comma 9 space см.

Адказ: r2 = 7,9 см.

Прыклад 2. Пунктавыя зарады q1 = 3,4 нКл і q2 = –5,6 нКл знаходзяцца ў вакууме на адлегласці r = 36 см. Вызначце модуль і напрамак уздзеяння рэзультуючай сілы на зарад q3 = 3,2 нКл, змешчаны ў пункт прасторы, які знаходзіцца на сярэдзіне адрэзка, што злучае гэтыя зарады.

Дадзена:
q1 = 3,4 нКл = 3,4 · 10–9 Кл
q2 = –5,6 нКл = –5,6 · 10–9 Кл
r = 36 см = 0,36 м
q3 = 3,2 нКл = 3,2 · 10–9 Кл
F with rightwards arrow on top subscript straight р — ?

Рашэнне. Адлюструем на малюнку сілы F with rightwards arrow on top subscript 13 і F with rightwards arrow on top subscript 23, якія дзейнічаюць на пунктавы зарад q3 з боку пунктавых зарадаў q1 i q2 адпаведна. Пабудаваўшы вектарную суму сіл F with rightwards arrow on top subscript 13 i F with rightwards arrow on top subscript 23, вызначым, што рэзультуючая F with rightwards arrow on top subscript straight р гэтых сіл накіравана да зараду q2 (мал. 102).

Паколькі сілы F with rightwards arrow on top subscript 13 i F with rightwards arrow on top subscript 23 накіраваны аднолькава, то модуль рэзультуючай сілы F subscript straight р equals F subscript 13 plus F subscript 23 equals fraction numerator 4 k q subscript 3 over denominator r squared end fraction left parenthesis q subscript 1 plus open vertical bar q subscript 2 close vertical bar right parenthesis.

Такім чынам,

F subscript straight р equals fraction numerator 4 times 9 comma 0 times 10 to the power of 9 space begin display style fraction numerator straight Н times straight м squared over denominator Кл squared end fraction end style times 3 comma 2 times 10 to the power of negative 9 end exponent space Кл over denominator left parenthesis 0 comma 36 space straight м right parenthesis squared end fraction times left parenthesis 3 comma 4 times 10 to the power of negative 9 end exponent space Кл plus 5 comma 6 times 10 to the power of negative 9 end exponent space Кл right parenthesis equals 8 comma 0 times 10 to the power of negative 6 end exponent space straight Н equals 8 comma 0 space мкН.

Адказ: Fp = 8,0 мкН; сіла накіравана да заряду q2.

Адсылка да электроннага дадатку для павышанага ўзроўню

Прыклад 3. Дзве пацеркі, электрычныя зарады якіх q1 = 40 нКл i q2 = 90 нКл, замацаваны на неправодным стрыжні на адлегласці r = 40 см адна ад адной. Вызначце: а) дзе трэба размясціць трэцюю пацерку, якая мае зарад q3, каб яна была ў раўнавазе; б) якім павінен быць зарад q3 трэцяй пацеркі, каб рэзультуючая сіла электрастатычнага ўзаемадзеяння кожнай з трох пацерак з іншымі дзвюма была роўная нулю.

Дадзена:
q1 = 40 нКл = 4,0·10–8 Кл
q2 = 90 нКл = 9,0·10−8 Кл
r = 40 см = 0,40 м
х — ?
q3 — ?

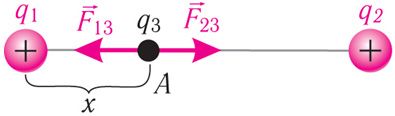
Рашэнне. а) Трэцяя пацерка, якая мае зарад q3, будзе знаходзіцца ў раўнавазе, калі яе змясціць у некаторы пункт А паміж зарадамі q1 i q2 на прамой, што злучае гэтыя зарады (мал. 102.1). Няхай зарад q3 < 0. Тады з боку зарадаў q1 i q2 на зарад q3 будуць дзейнічаць супрацьлегла накіраваныя кулонаўскія сілы прыцяжэння F with rightwards arrow on top subscript 13 i F with rightwards arrow on top subscript 23. Згодна з другім законам Ньютана гэтая пацерка будзе знаходзіцца ў спакоі, калі модулі сіл F13 i F23 роўныя. Тады, прыняўшы адлегласць ад зараду q1 да пункта А роўнай х, запішам: k fraction numerator q subscript 1 open vertical bar q subscript 3 close vertical bar over denominator x squared end fraction equals k fraction numerator q subscript 2 open vertical bar q subscript 3 close vertical bar over denominator open parentheses r minus x close parentheses squared end fraction. Паколькі k i q3 не роўныя нулю, то гэты выраз можна скараціць: q subscript 1 over x squared equals q subscript 2 over open parentheses r minus x close parentheses squared. Здабудзем з абедзвюх частак роўнасці квадратны корань open parentheses x greater than 0 comma space r minus x greater than 0 close parentheses colon space fraction numerator square root of q subscript 1 end root over denominator x end fraction equals fraction numerator square root of q subscript 2 end root over denominator r minus x end fraction. Адсюль:

x equals fraction numerator square root of q subscript 1 end root times r over denominator square root of q subscript 1 end root plus square root of q subscript 2 end root end fraction.

x equals fraction numerator square root of 4 comma 0 times 10 to the power of negative 8 end exponent space Кл end root times 0 comma 40 space straight м over denominator square root of 4 comma 0 times 10 to the power of negative 8 end exponent space Кл end root plus square root of 9 comma 0 times 10 to the power of negative 8 end exponent space Кл end root end fraction equals 0 comma 16 space straight м.

Мал.
Мал. 102.1
Мал.
Мал. 102.2

Такое ж значэнне х мы атрымаем, калі прымем, што зарад q3 пацеркі дадатны (праверце гэта самастойна).

б) Рэзультуючая сіла электрастатычнага ўзаемадзеяння кожнай з трох пацерак з іншымі дзвюма роўная нулю, калі, напрыклад, трэцяя пацерка прыцягвае другую сілай, модуль open vertical bar F with rightwards arrow on top subscript 32 close vertical bar якой роўны модулю сілы open vertical bar F with rightwards arrow on top subscript 12 close vertical bar, якой яе адштурхвае першая пацерка (мал. 103.2). Пры гэтым зарад трэцяй пацеркі павінен быць адмоўным, гэта значыць q3 < 0. Тады k fraction numerator q subscript 1 q subscript 2 over denominator r squared end fraction equals k fraction numerator q subscript 2 open vertical bar q subscript 3 close vertical bar over denominator open parentheses r minus x close parentheses squared end fraction. Адсюль open vertical bar q subscript 3 close vertical bar equals open parentheses r minus x close parentheses squared over r squared q subscript 1.

open vertical bar q subscript 3 close vertical bar equals open parentheses 0 comma 24 space straight м close parentheses squared over open parentheses 0 comma 44 space straight м close parentheses squared times 4 comma 0 times 10 to the power of negative 8 end exponent space Кл equals 1 comma 4 times 10 to the power of negative 8 end exponent space Кл space equals 14 space нКл.

Адказ: х = 16 см, адлегласць да пацеркі з зарадам q3 не залежыць ад значэння і знака яе зараду; калі зарад пацеркі q3 = –14 нКл, то рэзультуючая сіла электрастатычнага ўзаемадзеяння кожнай з трох пацерак з іншымі дзвюма роўная нулю.

Рис.
Рис. 102.3

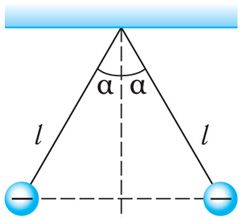
Прыклад 4. Два аднолькавыя праводныя маленькія шарыкі масай m = 20 мг кожны падвешаны ў паветры на лёгкіх нерасцяжных нітках даўжынёй l = 0,20 м, замацаваных у адным пункце падвесу. Адзін з шарыкаў адвялі ў бок, надалі яму зарад q < 0 і адпусцілі. Пасля сутыкнення шарыкі разышліся так, што вугал паміж ніткамі склаў 2α = 60° (мал. 102.3). Вызначце зарад, які быў нададзены першаму шарыку, а таксама колькасць залішніх электронаў на кожным з шарыкаў пасля іх сутыкнення.

Дадзена:
m = 20 мг = 2,0 · 10–5 кг
l = 0,20 м
2α = 60°
q — ?
N — ?

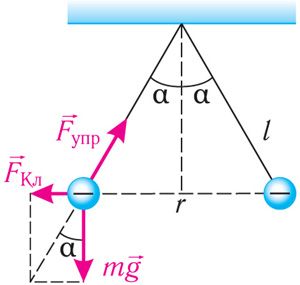
Рашэнне. Выкарыстаем закон захавання электрычнага зараду. Падчас сутыкнення двух аднолькавых праводных шарыкаў нададзены аднаму з іх зарад падзяліўся пароўну, і на кожным шарыку аказаўся залішні адмоўны зарад q subscript 1 equals q subscript 2 equals q over 2. На кожны шарык дзейнічаюць сіла цяжару F with rightwards arrow on top subscript straight ц equals m with rightwards arrow on top g, сіла электрастатычнага ўзаемадзеяння F with rightwards arrow on top subscript Кл і сіла пругкасці ніткі F with rightwards arrow on top subscript упр (мал. 102.4). Пасля сутыкнення шарыкі разышліся, і ўстанавілася раўнавага. Вектарная сума сіл, якія дзейнічаюць на кожны шарык, стала роўная нулю: m g with rightwards arrow on top plus F with rightwards arrow on top subscript Кл plus F with rightwards arrow on top subscript упр equals 0 with rightwards arrow on top. Модуль сілы электрастатычнага ўзаемадзеяння F subscript Кл equals k fraction numerator open vertical bar q subscript 1 close vertical bar times open vertical bar q subscript 2 close vertical bar over denominator r squared end fraction equals fraction numerator k q squared over denominator 4 r squared end fraction. Паколькі шарыкі разышліся сіметрычна адносна вертыкалі, што праходзіць праз пункт падвеса нітак, то fraction numerator r over denominator 2 l end fraction equals sin straight alpha (мал. 102.4). Такім чынам, F subscript Кл equals fraction numerator k q squared over denominator 16 l squared sin squared straight alpha end fraction. Паколькі fraction numerator F subscript Кл over denominator m g end fraction equals tg straight alpha, то fraction numerator k q squared over denominator 16 l squared sin squared straight alpha end fraction equals m g tg straight alpha, адкуль open vertical bar q close vertical bar equals 4 l sin straight alpha square root of fraction numerator m g tg straight alpha over denominator k end fraction end root. Прымем k equals 9 comma 0 times 10 to the power of 9 space fraction numerator straight Н times straight м squared over denominator Кл squared end fraction.

Мал.
Мал. 102.4

open vertical bar q close vertical bar equals 4 times 0 comma 20 space straight м times 0 comma 50 square root of fraction numerator 2 comma 0 times 10 to the power of negative 5 end exponent space кг space times 9 comma 8 begin display style straight м over straight с squared end style times 0 comma 58 over denominator 9 comma 0 times 10 to the power of 9 space begin display style fraction numerator straight Н times straight м squared over denominator Кл squared end fraction end style end fraction end root equals 4 comma 5 times 10 to the power of negative 8 end exponent space Кл equals 45 space нКл.

Колькасць залішніх электронаў на кожным шарыку N equals fraction numerator open vertical bar q close vertical bar over denominator 2 e end fraction.

N equals fraction numerator 4 comma 5 times 10 to the power of negative 8 end exponent space Кл over denominator 2 times 1 comma 6 times 10 to the power of negative 19 end exponent space Кл end fraction equals 1 comma 4 times 10 to the power of 11.

Адказ: q = ‒45 нКл, N = 1,4 · 1011.