§ 17. Узаемадзеянне пунктавых зарадаў. Закон Кулона
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 10 клас |
| Книга: | § 17. Узаемадзеянне пунктавых зарадаў. Закон Кулона |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 6 Июль 2025, 08:36 |
Электрычна зараджаныя целы (часціцы) узаемадзейнічаюць адно з адным. Але як вызначыць сілу, з якой адно зараджанае цела прыцягвае або адштурхвае другое?
Вы ўжо сустракаліся з фізічнымі мадэлямі пры вывучэнні механікі (матэрыяльны пункт) і малекулярнай фізікі (ідэальны газ). У электрастатыцы пры вывучэнні ўзаемадзеяння электрычна зараджаных цел эфектыўнай з’яўляецца мадэль «пунктавы зарад».
Пунктавы зарад — зарад такога зараджанага цела, памеры якога значна меншыя за адлегласць ад гэтага цела да пункта назірання і да іншых цел (гэта значыць памеры зараджанага цела ва ўмовах дадзенай задачы можна не прымаць пад увагу).
Успомніце, закон сусветнага прыцягнення таксама сфармуляваны для пунктавых цел (матэрыяльных пунктаў).
Закон Кулона. Кулон дэталёва даследаваў узаемадзеянне нерухомых пунктавых зарадаў. Ён шляхам доследаў вывучыў залежнасць сіл электрычнага ўзаемадзеяння цел ад модуляў зарадаў гэтых цел і адлегласці паміж імі.
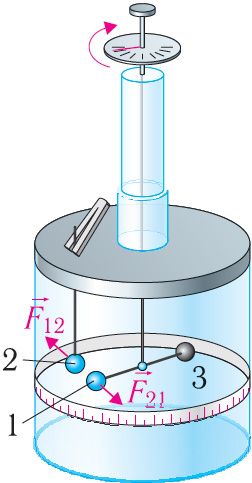
У сваіх доследах Кулон выкарыстоўваў спецыяльную прыладу — круцільныя вагі (мал. 98). Круцільныя вагі ўяўляюць з сябе два шкляныя цыліндры, унутры якіх на тонкай сярэбранай нітцы падвешаны лёгкі неправодны каромысел. На адным канцы каромысла замацаваны праводны шар 1, а на другім — папяровая процівага 3. Шар 1 можна зараджаць з дапамогай такога самага праводнага шара 2. Ён знаходзіцца на ізалюючым стрыжні, які замацаваны на накрыўцы ніжняга цыліндра. У час судакранання шара 1 з зараджаным шарам 2 зарад размяркоўваецца паміж імі пароўну, і шары адштурхваюцца.
![]()
Выкарыстоўваючы круцільныя вагі, Кулон атрымаў залежнасць модуля сіл узаемадзеяння двух зараджаных шароў ад велічынь зарадаў і ад адлегласці паміж імі. Паводле вугла закручвання ніткі, які адлічваецца па шкале прыбора, можна вызначыць сілу ўзаемадзеяння зараджаных шароў . Кулон вызначыў, што модуль сіл узаемадзеяння двух зараджаных шароў адваротна прапарцыянальны квадрату адлегласці паміж імі:
.
Для вымярэння залежнасці модуля сіл узаемадзеяння шароў ад іх зарадаў вучоны знайшоў просты спосаб. Разраджаючы шар 2 дотыкам рукі, а затым дакранаючыся ім да ўжо зараджанага шара 1, Кулон змог атрымаць на ім зарады, модуль якіх быў у 2, 4, 8 і г. д. разоў меншы за першапачатковы. Ён высветліў, што пры нязменнай адлегласці модуль сіл узаемадзеяння двух нерухомых невялікіх зараджаных цел прама прапарцыянальны здабытку модуляў электрычных зарадаў кожнага з іх: .
Абагульніўшы эксперыментальныя даныя, Кулон сфармуляваў закон, які атрымаў яго імя.
Закон Кулона: модулі сіл узаемадзеяння двух нерухомых пунктавых зараджаных цел у вакууме прама прапарцыянальныя здабытку модуляў зарадаў гэтых цел, адваротна прапарцыянальныя квадрату адлегласці паміж імі, а самі сілы накіраваны ўздоўж прамой, якая злучае гэтыя целы:
(17.1)
дзе k — каэфіцыент прапарцыянальнасці, які залежыць ад выбару адзінак фізічных велічынь; |q1| і |q2| — модулі пунктавых зарадаў; r — адлегласць паміж імі.
У СІ каэфіцыент прапарцыянальнасці
дзе — электрычная пастаянная.
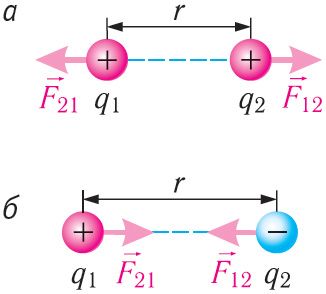
Сілы і
узаемадзеяння нерухомых пунктавых зарадаў (мал. 99) называюць кулонаўскімі сіламі. У адпаведнасці з трэцім законам Ньютана гэтыя сілы супрацьлегла накіраваныя
, а іх модулі роўныя. Адзначым, што сілы электрастатычнага ўзаемадзеяння з’яўляюцца сіламі адштурхвання для аднайменных зарадаў (мал. 99, а) і сіламі прыцяжэння для розна іменных (мал. 99, б).
Два маленькія дадатна зараджаныя шарыкі замацаваны на адлегласці r адзін ад аднаго. Як зменіцца модуль сіл электрастатычнага ўзаемадзеяння шарыкаў, калі: 1) паменшыць зарад кожнага шарыка ў чатыры разы; 2) павялічыць адлегласць паміж шарыкамі ў чатыры разы; 3) павялічыць зарад кожнага шарыка і адлегласць паміж імі ў два разы?
Як змяніліся б сілы электрастатычнага ўзаемадзеяння шарыкаў, калі б: 1) шарыкі былі зараджаныя адмоўна; 2) адзін з шарыкаў зараджаны адмоўна, а другі дадатна?
![]()
Цікава ведаць
Эксперыментальныя факты сведчаць пра тое, што ўздзеянне нерухомага у дадзенай інерцыяльнай сістэме адліку пунктавага зараду на пунктавы зарад, які рухаецца, можна апісаць законам Кулона з прымальнай дакладнасцю. Так, апісанне рассеяння α-частиц на ядрах атамаў золата ў доследах Рэзерфорда з дапамогай мадэлі пунктавага зараду, на які дзейнічае кулонаўская сіла з боку нерухомага ядра, адпавядае эксперыментальным даным у межах дакладнасці апошніх.
Два і больш зарадаў, якія рухаюцца ў дадзенай інерцыяльнай сістэме, не могуць характарызавацца толькі кулонаўскім узаемадзеяннем, бо кожны з іх стварае ў навакольнай прасторы магнітнае поле, якое дзейнічае магнітнай сілай на астатнія зарады, што рухаюцца ў ім.
Узаемадзеянне сістэмы пунктавых зарадаў. Эксперыментальным шляхам вызначылі, што сілы ўзаемадзеяння двух пунктавых зарадаў не змяняюцца пры з’яўленні трэцяга пунктавага зараду або любой колькасці пунктавых зарадаў. У гэтым выпадку сілы ўздзеяння ,
, ...,
кожнага з зарадаў q2, q3, …, qn на зарад q1 вызначаюць па законе Кулона. Рэзультуючая сіла з’яўляецца вектарнай сумай сіл, якімі кожны з гэтых зарадаў паасобку ўздзейнічае на зарад q1 (прынцып суперпазіцыі).
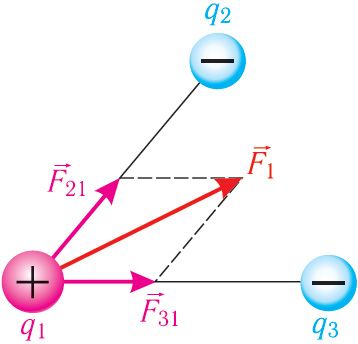
Выкарыстоўваючы прынцып суперпазіцыі і закон Кулона, можна апісаць электрастатычнае ўзаемадзеянне любой сістэмы пунктавых зарадаў. На малюнку 100 паказаны тры пунктавыя электрычныя зарады, якія ўзаемадзейнічаюць паміж сабой: q1 > 0, q2 < 0, q3 < 0. Рэзультуючай сіл, якія дзейнічаюць на зарад q1 з боку зарадаў q2 і q3, з’яўляецца сіла , роўная вектарнай суме сіл
і
:
. Сілы
и
уздзеяння зарадаў q2 і q3 на зарад q1 вызначаюць паводле закона Кулона.
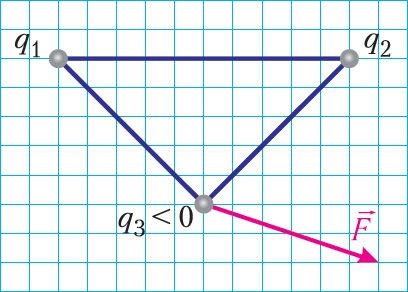
Пунктавыя зарады q1, q2 і q3 замацаваны ў вяршынях трохвугольніка. Напрамак рэзультуючай электрастатычнай сілы, якая дзейнічае на адмоўны зарад q3 з боку зарадаў q1 і q2, паказаны на малюнку 101. Якія знакі маюць зарады q1 і q2? У колькі разоў адрозніваюцца модулі зарадаў q1 і q2?
Цікава ведаць
Паняцце электрычнага зараду ў пэўнай ступені нагадвае паняцце гравітацыйнай масы. Электрычны зарад вызначае інтэнсіўнасць электрамагнітных узаемадзеянняў, а масса — гравітацыйных. Закон Кулона, які апісвае электрастатычнае ўзаемадзеянне, фармальна падобны на закон сусветнага прыцягнення Ньютана, які вызначае сілы гравітацыйнага ўзаемадзеяння:
У абодвух выпадках модуль сіл узаемадзеяння:
– адваротна прапарцыянальны квадрату адлегласці паміж матэрыяльнымі пунктамі;
– прама прапарцыянальны велічыням, якія характарызуюць тыя ўласцівасці цел (матэрыяльных пунктаў), якія вызначаюць узаемадзеянні, — масам у адным выпадку і электрычным зарадам — у другім.
Для вымярэння сіл электрычнага адштурхвання (Ш. Кулон, 1785) і гравітацыйнай пастаяннай (Г. Кавендыш, 1788 г.) вучоныя выкарыстоўвалі падобныя па будове эксперыментальныя прылады.
Аднак паміж сіламі гравітацыйнага і электрастатычнага ўзаемадзеянняў ёсць істотнае адрозненне. Ньютанаўскія сілы прыцягнення — гэта заўсёды сілы прыцяжэння. Кулонаўскія ж сілы ўзаемадзеяння зарадаў могуць быць як сіламі прыцяжэння (паміж рознаіменнымі зарадамі), так і сіламі адштурхвання (паміж аднайменнымі зарадамі).
![]()
Вядома, што маса электрона mе = 9,1 · 10–31 кг. У колькі разоў модуль сіл электрычнага адштурхвання паміж двума электронамі большы, чым модуль сіл іх гравітацыйнага прыцяжэння?
Дыэлектрычная пранікальнасць рэчыва. З доследаў вынікае, што ўзаемадзеянне электрычна зараджаных цел у паветры практычна не адрозніваецца ад іх узаемадзеяння ў вакууме. Калі зараджаныя целы знаходзяцца ў вадзе, газе, алеі або якім-небудзь іншым неправодным асяроддзі, то модуль сіл іх узаемадзеяння будзе меншы, чым у вакууме. Каб улічыць уплыў асяроддзя, увялі яго адмысловую характарыстыку, названую дыэлектрычнай пранікальнасцю.
Дыэлектрычная пранікальнасць рэчыва — фізічная велічыня, якая паказвае, у колькі разоў модуль сіл электрастатычнага ўзаемадзеяння зарадаў у дадзеным аднародным асяроддзі меншы, чым модуль сіл узаемадзеяння гэтых жа зарадаў у вакууме:
(17.2)
дзе F0 і F — модулі сіл электрастатычнага ўзаемадзеяння зарадаў у вакууме і ў аднародным асяроддзі адпаведна.
З улікам суадносін (17.2) закон Кулона можна запісаць наступным чынам:
Дыэлектрычная пранікальнасць вакууму роўная 1. За 1 прымаюць і дыэлектрычную пранікальнасць паветра, бо яна мае значэнне (пры нармальным атмасферным ціску) 1,0006. Дыэлектрычныя пранікальнасці іншых аднародных асяроддзяў заўсёды большыя за адзінку. Напрыклад, дыэлектрычная пранікальнасць вады 81, гліцэрыны — 56, а газы — 2.
Як і ў колькі разоў адрозніваюцца модулі сіл электрастатычнага ўзаемадзеяння двух пунктавых зарадаў, якія знаходзяцца на аднолькавай адлегласці адзін ад аднаго ў вадзе, газе і гліцэрыне?
Цікава ведаць
Дыэлектрычная пранікальнасць дыстыляванай вады пры тэмпературы 25 °С роўная 78,54, а пры тэмпературы 0 °С — 88. Звычайна без указання тэмпературы дыэлектрычную пранікальнасць вады лічаць роўнай 81.

1. Да якога віду ўзаемадзеянняў адносяць узаемадзеянне нерухомых электрычных зарадаў (зараджаных цел)?
2. Зарады якіх зараджаных цел можна лічыць пунктавымі?
3. Раскажыце пра эксперыменты Кулона па даследаванні ўзаемадзеяння электрычных зарадаў.
4. Сфармулюйце закон Кулона. Якія ўмовы прымяняльнасці закона Кулона?
5. Чаму роўны ў СІ каэфіцыент k? Выразіце найменне каэфіцыента прапарцыянальнасці k у законе Кулона ў асноўных адзінках СІ.
6. У чым сутнасць прынцыпу суперпазіцыі для электрычнага ўзаемадзеяння пунктавых зарадаў?
7. Што называюць дыэлектрычнай пранікальнасцю асяроддзя?
![]()
Прыклад 1. Два пунктавыя зарады знаходзяцца ў газе на адлегласці r1 = 42 см. Вызначце, на якой адлегласці павінны знаходзіцца гэтыя зарады ў гліцэрыне, каб модуль сіл іх электрастатычнага ўзаемадзеяння застаўся ранейшы. Дыэлектрычныя пранікальнасці газы ε1 = 2,0, гліцэрыны ε2 = 56,2.
r1 = 42 см
Fк1 = Fк2
ε1 = 2,0
ε2 = 56,2
Рашэнне. Паколькі Fк1 = Fк2, то, выкарыстаўшы закон Кулона, можна запісаць: .
Значыць, .
Адказ: r2 = 7,9 см.
Прыклад 2. Пунктавыя зарады q1 = 3,4 нКл і q2 = –5,6 нКл знаходзяцца ў вакууме на адлегласці r = 36 см. Вызначце модуль і напрамак уздзеяння рэзультуючай сілы на зарад q3 = 3,2 нКл, змешчаны ў пункт прасторы, які знаходзіцца на сярэдзіне адрэзка, што злучае гэтыя зарады.
q1 = 3,4 нКл = 3,4 · 10–9 Кл
q2 = –5,6 нКл = –5,6 · 10–9 Кл
r = 36 см = 0,36 м
q3 = 3,2 нКл = 3,2 · 10–9 Кл
Рашэнне. Адлюструем на малюнку сілы і
, якія дзейнічаюць на пунктавы зарад q3 з боку пунктавых зарадаў q1 i q2 адпаведна. Пабудаваўшы вектарную суму сіл
i
, вызначым, што рэзультуючая
гэтых сіл накіравана да зараду q2 (мал. 102).
Паколькі сілы i
накіраваны аднолькава, то модуль рэзультуючай сілы
.
Такім чынам,
Адказ: Fp = 8,0 мкН; сіла накіравана да заряду q2.
![]()
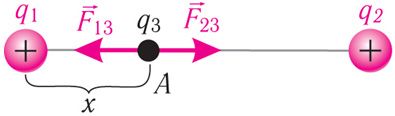
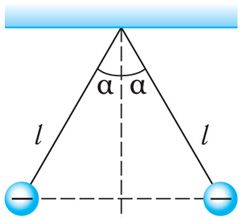
Прыклад 3. Дзве пацеркі, электрычныя зарады якіх q1 = 40 нКл i q2 = 90 нКл, замацаваны на неправодным стрыжні на адлегласці r = 40 см адна ад адной. Вызначце: а) дзе трэба размясціць трэцюю пацерку, якая мае зарад q3, каб яна была ў раўнавазе; б) якім павінен быць зарад q3 трэцяй пацеркі, каб рэзультуючая сіла электрастатычнага ўзаемадзеяння кожнай з трох пацерак з іншымі дзвюма была роўная нулю.
q1 = 40 нКл = 4,0·10–8 Кл
q2 = 90 нКл = 9,0·10−8 Кл
r = 40 см = 0,40 м
q3 — ?
Рашэнне. а) Трэцяя пацерка, якая мае зарад q3, будзе знаходзіцца ў раўнавазе, калі яе змясціць у некаторы пункт А паміж зарадамі q1 i q2 на прамой, што злучае гэтыя зарады (мал. 102.1). Няхай зарад q3 < 0. Тады з боку зарадаў q1 i q2 на зарад q3 будуць дзейнічаць супрацьлегла накіраваныя кулонаўскія сілы прыцяжэння i
. Згодна з другім законам Ньютана гэтая пацерка будзе знаходзіцца ў спакоі, калі модулі сіл F13 i F23 роўныя. Тады, прыняўшы адлегласць ад зараду q1 да пункта А роўнай х, запішам:
. Паколькі k i q3 не роўныя нулю, то гэты выраз можна скараціць:
. Здабудзем з абедзвюх частак роўнасці квадратны корань
. Адсюль:
Такое ж значэнне х мы атрымаем, калі прымем, што зарад q3 пацеркі дадатны (праверце гэта самастойна).
б) Рэзультуючая сіла электрастатычнага ўзаемадзеяння кожнай з трох пацерак з іншымі дзвюма роўная нулю, калі, напрыклад, трэцяя пацерка прыцягвае другую сілай, модуль якой роўны модулю сілы
, якой яе адштурхвае першая пацерка (мал. 103.2). Пры гэтым зарад трэцяй пацеркі павінен быць адмоўным, гэта значыць q3 < 0. Тады
. Адсюль
.
Адказ: х = 16 см, адлегласць да пацеркі з зарадам q3 не залежыць ад значэння і знака яе зараду; калі зарад пацеркі q3 = –14 нКл, то рэзультуючая сіла электрастатычнага ўзаемадзеяння кожнай з трох пацерак з іншымі дзвюма роўная нулю.
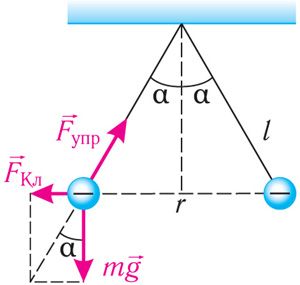
Прыклад 4. Два аднолькавыя праводныя маленькія шарыкі масай m = 20 мг кожны падвешаны ў паветры на лёгкіх нерасцяжных нітках даўжынёй l = 0,20 м, замацаваных у адным пункце падвесу. Адзін з шарыкаў адвялі ў бок, надалі яму зарад q < 0 і адпусцілі. Пасля сутыкнення шарыкі разышліся так, што вугал паміж ніткамі склаў 2α = 60° (мал. 102.3). Вызначце зарад, які быў нададзены першаму шарыку, а таксама колькасць залішніх электронаў на кожным з шарыкаў пасля іх сутыкнення.
m = 20 мг = 2,0 · 10–5 кг
l = 0,20 м
2α = 60°
N — ?
Рашэнне. Выкарыстаем закон захавання электрычнага зараду. Падчас сутыкнення двух аднолькавых праводных шарыкаў нададзены аднаму з іх зарад падзяліўся пароўну, і на кожным шарыку аказаўся залішні адмоўны зарад . На кожны шарык дзейнічаюць сіла цяжару
, сіла электрастатычнага ўзаемадзеяння
і сіла пругкасці ніткі
(мал. 102.4). Пасля сутыкнення шарыкі разышліся, і ўстанавілася раўнавага. Вектарная сума сіл, якія дзейнічаюць на кожны шарык, стала роўная нулю:
. Модуль сілы электрастатычнага ўзаемадзеяння
. Паколькі шарыкі разышліся сіметрычна адносна вертыкалі, што праходзіць праз пункт падвеса нітак, то
(мал. 102.4). Такім чынам,
. Паколькі
, то
, адкуль
. Прымем
.
Колькасць залішніх электронаў на кожным шарыку .
Адказ: q = ‒45 нКл, N = 1,4 · 1011.
Практыкаванне 13
1. Вызначце модуль сіл узаемадзеяння двух аднолькавых нерухомых пункта вых зарадаў q1 = q2 = 9,0 нКл, якія знаходзяцца на адлегласці r = 0,30 м у ваку уме. У колькі разоў паменшыцца ці павялічыцца модуль сіл узаемадзеяння гэтых зарадаў, калі змясціць іх у газу, дыэлектрычная пранікальнасць якой ε = 2,0?
2. Вызначце, у колькі разоў трэба павялічыць адлегласць паміж двума нерухомымі пунктавымі зарадамі, каб модуль сіл узаемадзеяння застаўся ранейшым пры павелічэнні колькаснага значэння аднаго з зарадаў α = 4 разы.
3. Два аднолькавыя маленькія праводныя шарыкі, зарады якіх адрозні ваюцца ў два разы, знаходзяцца на адлегласці r = 50 см. Вызначце адлегласць, на якую неабходна развесці шарыкі пасля судакранання, каб модуль сіл іх узаемадзеяння застаўся ранейшым.
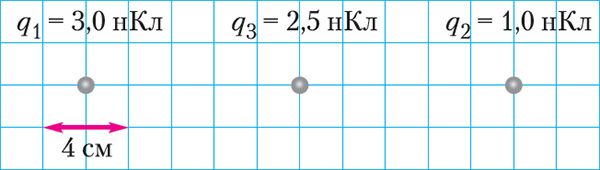
4. Пунктавыя зарады q1 і q2 замацаваны ў вакууме (мал. 103). Вызначце модуль і напрамак рэзультуючай сілы, якая дзейнічае на зарад q3, змешчаны ў пункт, які знаходзіцца на сярэдзіне адрэзка, што злучае гэтыя зарады.
5. Зарады двух аднолькавых маленькіх шарыкаў масай m = 40 г кожны аднолькавыя. Адлегласць паміж шарыкамі істотна перавышае іх памеры. Вызначце модуль зарадаў шарыкаў, калі кулонаўская сіла іх адштурхвання ўраўнаважвае сілу гравітацыйнага прыцяжэння гэтых шарыкаў.
6. Невялікі шарык, зарад якога q1 = 20 нКл і маса m = 60 мг, падвешаны ў паветры на шаўковай нітцы. Пасля таго як на вертыкалі, якая праходзіць праз цэнтр шарыка, на адлегласці r = 15 см ніжэй яго змясцілі другі маленькі шарык, зараджаны адмоўна, модуль сілы пругкасці ніткі павялічыўся ў два разы. Вызначце зарад другога шарыка.
![]()
7. Тры першапачаткова замацаваныя аднолькавыя пунктавыя зарады q1 = q2 = q3 = q0 = 1,0 мкКл размешчаны ў вяршынях роўнастаронняга трохвугольніка. Вызначце, які пунктавы зарад трэба змясціць у цэнтр трохвугольніка, каб уся сістэма знаходзілася ў раўнавазе пасля вызвалення першапачаткова замацаваных зарадаў.