§ 8. Вылічэнне значэння ліку π метадам Монтэ-Карла

8.3. Стварэнне дакументальнай матэматычнай мадэлі (этап 1)

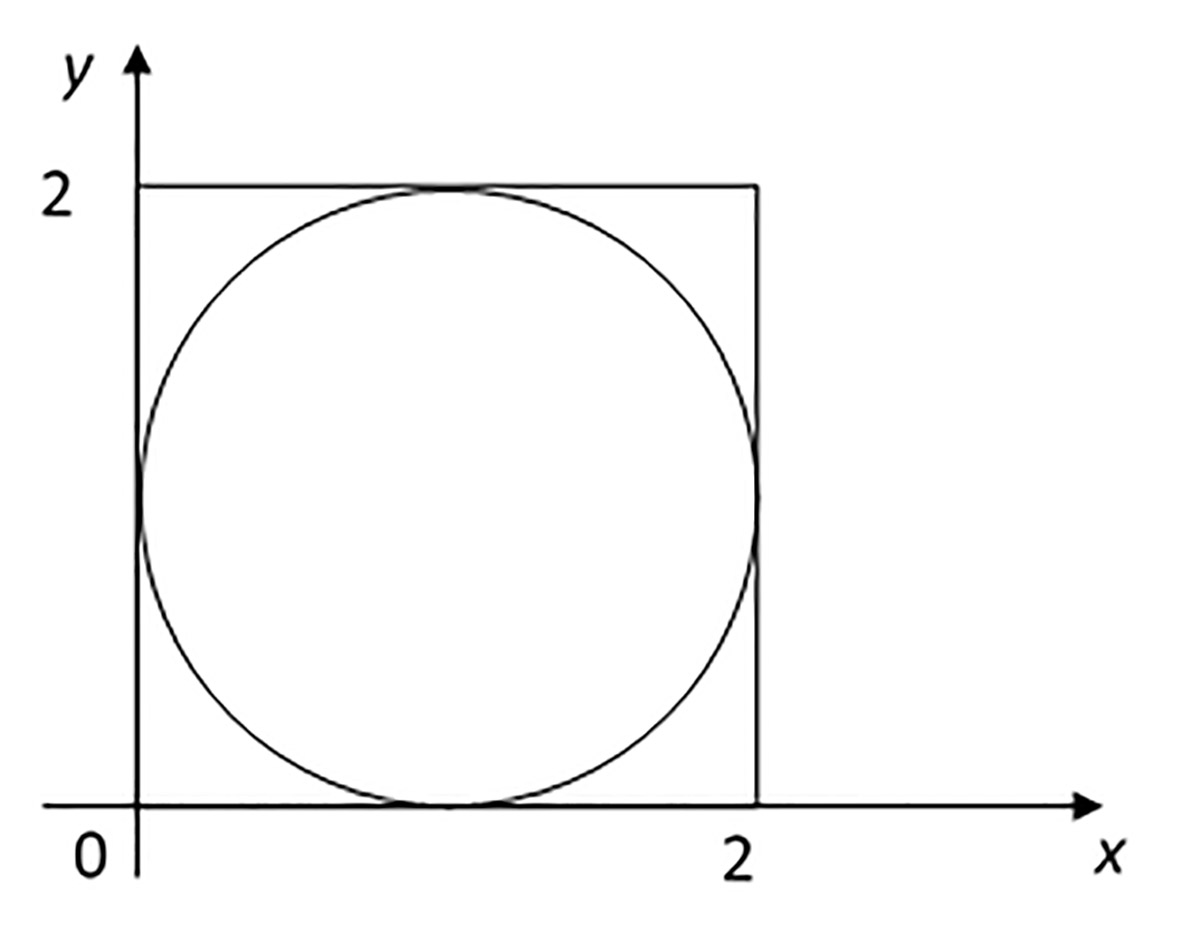
Так як значэнне радыусу круга абмежаванняў не мае, возьмем круг адзінкавага радыусу (r = 1). Тады мінімальны базавы прамавугольнiк будзе мець форму квадрата з бокам 2 (прыклад 8.1).

Плошча базавага квадрата S0 = 4.

Хай S — шуканая плошча круга.

Метадам Монтэ-Карла неабходна імітаваць працэс пасыпання базавага квадрата пунктамі-пясчынкамі, падлічваючы агульную колькасць n кропак і лік k кропак, якія трапілі ў круг (прыклад 8.2).

Для стварэння камп'ютарнай разліковай мадэлі можна выкарыстоўваць электронныя табліцы і мову праграміравання. Але ў электронных табліцах агульная колькасць n пунктаў будзе вызначацца лікам радкоў у разліковай табліцы, а ў праграме на мове Pascal — толькі лікам паўтораў цыклу. Таму выбіраем сістэму PascalABC.NET.

Прыклад 8.1. Пабудуем базавы квадрат i круг у прамавугольнай сiстэме каардынат наступным чынам.

Пример 8.2. Для вылічэння плошчы круга будзем выкарыстоўваць асноўную формулу метаду Монтэ-Карла . У нашым выпадку .

Для вылічэння значэння лiку  скарыстаемся выведзенай раней формулай , якая для адзінкавага круга атрымае выгляд . Выявілася, што для вылічэння значэння лiку  дастаткова вылічыць плошчу адзінкавага круга.