Печатать книгуПечатать книгу

§ 8. Вылічэнне значэння ліку π метадам Монтэ-Карла

Сайт: Профильное обучение
Курс: Інфармацыйныя тэхналогіі. 11 клас (Базавы ўзровень)
Книга: § 8. Вылічэнне значэння ліку π метадам Монтэ-Карла
Напечатано:: Гость
Дата: Пятница, 4 Апрель 2025, 16:40

Оглавление

8.1. Пастаноўка задачы (этап 1)

Задача. Метадам Монтэ-Карла вылічыць значэнне лiку .
Вядома больш за 15 метадаў вылічэння значэння лiку .

8.2. Выбар плана стварэння мадэлі (этап 2)

Геаметрычны метад Монтэ-Карла дазваляе вылiчыць плошчы плоскiх фiгур. Калi гэтым метадам знайсцi плошчу круга  зададзеннага радыусу , то, карыстаючыся вядомай формулай , можно знайсцi значэнне

.

Абярэм наступны план стварэння маделi:

3а) стварэнне дакументальнай матэматычнай мадэлі;
3б) стварэнне дакументальнай разліковай мадэлі;
3в) стварэнне камп'ютарнай разлiковай мадэлi.

Для вылiчэння плошчы круга варта пабудаваць чарцёж круга и базавага прамавугольнiка, падабраць формулы, таму спачатку будзем будаваць дакументальную матэматычную мадэль.

Затым варта падабраць падыходны праграмны сродак для стварэння камп'ютарнай мадэлi i пабудаваць формулы для камп'ютарных разлiкаў. Гэта азначае, што трэба стварыць дакументальную разлiковую мадэль.

У заключэнні разліковую мадэль трэба рэалізаваць на камп'ютары, г. зн. стварыць камп'ютарную мадэль.

8.3. Стварэнне дакументальнай матэматычнай мадэлі (этап 1)

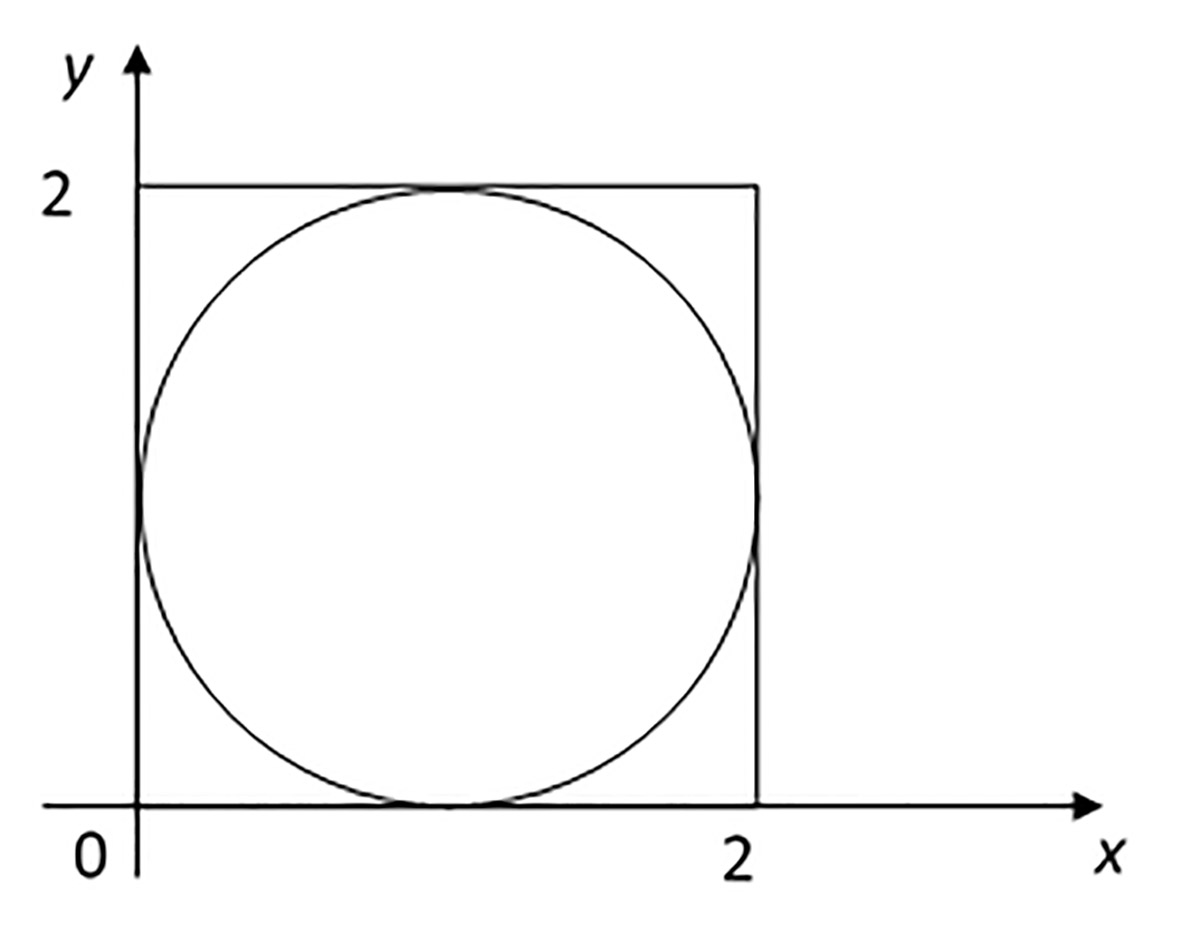
Так як значэнне радыусу круга абмежаванняў не мае, возьмем круг адзінкавага радыусу (r = 1). Тады мінімальны базавы прамавугольнiк будзе мець форму квадрата з бокам 2 (прыклад 8.1).

Плошча базавага квадрата S0 = 4.

Хай S — шуканая плошча круга.

Метадам Монтэ-Карла неабходна імітаваць працэс пасыпання базавага квадрата пунктамі-пясчынкамі, падлічваючы агульную колькасць n кропак і лік k кропак, якія трапілі ў круг (прыклад 8.2).

Для стварэння камп'ютарнай разліковай мадэлі можна выкарыстоўваць электронныя табліцы і мову праграміравання. Але ў электронных табліцах агульная колькасць n пунктаў будзе вызначацца лікам радкоў у разліковай табліцы, а ў праграме на мове Pascal — толькі лікам паўтораў цыклу. Таму выбіраем сістэму PascalABC.NET.

Прыклад 8.1. Пабудуем базавы квадрат i круг у прамавугольнай сiстэме каардынат наступным чынам.

Пример 8.2. Для вылічэння плошчы круга будзем выкарыстоўваць асноўную формулу метаду Монтэ-Карла . У нашым выпадку .

Для вылічэння значэння лiку  скарыстаемся выведзенай раней формулай , якая для адзінкавага круга атрымае выгляд . Выявілася, што для вылічэння значэння лiку  дастаткова вылічыць плошчу адзінкавага круга.

8.4. Стварэнне дакументальнай разліковай мадэлі (этап 2)

У праграме на мове Pascal варта арганізаваць цыкл for з лікам паўтораў n і ў ім генерыраваць выпадковыя каардынаты x і y пунктаў на базавым квадраце (прыклад 8.3).

Для падліку колькасці пунктаў, якія трапілі на адзінкавы круг, у цыкле варта выкарыстоўваць аператар if з умовай (x – 1)2 + (y – 1)2 ≤ 1 траплення пункту ў круг і пры выкананні гэтай умовы аператарам k:=k+1 арганізаваць накапленне значэнняў пераменнай k, як лічыльніка. Пасля цыкла неабходна арганізаваць вывядзенне выніку на экран (прыклад 8.4).

Прыклад 8.3. Для генерацыі каардынатаў пунктаў скарыстаемся функцыяй random (). Функцыя генерыруе выпадковыя сапраўдныя лікі ад 0 да 1, а каардынаты пунктаў-пясчынак на базавым квадраце павінны прымаць значэнні ад 0 да 2. Тады каардынаты пунктаў трэба вылічыць, выкарыстоўваючы выраз 2*random().

Прыклад 8.4. Для параўнання выведзем на экран разлічанае значэнне ліку  і фактычнае значэнне, якое захоўваецца ў сістэме PascalABC.NET як значэнне пераменнай з імем pi.

8.5. Стварэнне камп'ютарнай разліковай мадэлі (этап 3)

У сістэме PascalABC.NET аб'явім пераменныя n і k тыпу integer для захоўвання колькасці пунктаў-пясчынак на базавым квадраце і на крузе адпаведна, а таксама пераменныя s, x і y тыпу real для захоўвання значэнняў плошчы круга і каардынатаў пунктаў-пясчынак адпаведна.

У асноўным раздзеле праграмы, задаем пачатковыя значэннi і арганізуем цыкл (пример 8.5). Далей падлічваем вынік, выводзім яго і дакладнае значэнне лiку p на экран:

s := 4 * k / n;
writeln('Вынiк pi = ',s);
writeln('Дакладна pi = ',pi);

Прыклад 8.5. Задаем пачатковыя значэннi:

n := 1000;
k := 0;

У цыкле for з пачатковым значэннем пераменнай цыклу 1 і канчатковым значэннем n надаем выпадковыя значэннi каардынатам чарговага пункту:

x := 2 * random();
y := 2 * random();

З дапамогай умоўнага аператара if арганізуем падлік колькасці k пунктаў, якія трапілі ў круг:

if sqr(x-1)+sqr(y-1)<=1 then k:=k+1;

Засталося падлічыць плошчу круга па асноўнай формуле метаду.

8.6. Праверка адэкватнасці мадэлі (этап 4)

Адэкватнасць мадэлі правяраецца параўнаннем атрыманага значэння ліку p з дакладным. Пры колькасці паўтораў 1000 разлічанае значэнне павінна знаходзіцца ў межах ад 3,0 да 3,3 (прыклад 8.6).

Прыклад 8.6. Кожны новы запуск праграмы мяняе разлічанае значэнне, так як кожны раз выкарыстоўваецца новы набор з 1000 пунктаў-пясчынак з іншымі выпадковымі каардынатамі.

8.7. Атрыманне рашэння задачы з дапамогай мадэлі (этап 5)

У выніку некалькіх запускаў праграмы можна заўважыць, што для ліку p дакладна вызначаецца толькі цэлая частка значэння — лiк 3.

Удакладніць вынік дазваляе павелічэнне колькасці n пунктаў-пясчынак. Тэарэтычна, калі павялічыць лік n пунктаў-пясчынак у 100 разоў, дакладнасць выніку павялічыцца на 1 дзесятковы разрад направа (прыклад 8.7).

Прыклад 8.7. Павялічым лік n у 100 разоў, дапісваючы ў праграме нулі ў яго значэнні справа. У выніку некалькіх запускаў праграмы можна пераканацца, што ў значэнні ліку p вызначаюцца ўжо два разраду — 3,1.

Павялічым лік n яшчэ ў 100 разоў. Дакладнасць вылічэнняў павялічваецца да трох разрадаў — 3,14. Але пры гэтым расце і час выканання праграмы.

Практыкаваннi

  

1. Пералічыце этапы мадэлявання ў задачы вылічэння значэння ліку p метадам Монтэ-Карла.

2. Увядзіце тэкст праграмы montekarlo1 у сістэму PascalABC.NET у адпаведнасці з указаннямі, прыведзенымі ў параграфе.

3. Правядзіце этапы 4 і 5 мадэлявання ў адпаведнасці з указаннямі, прыведзенымі ў параграфе.

4. Стварыце мадэль для вылічэння значэння ліку p метадам Монтэ-Карла ў электронных табліцах, пабудаваўшы рабочую табліцу памерам у 1000 радкоў для падліку колькасці k. Параўнайце вынік з атрыманым раней.