§ 3. Ператварэнні энергіі пры гарманічных ваганнях
Практыкаванне 3
1. У якіх пунктах траекторыі пры ваганнях матэматычнага маятніка максімальная энергія:
а) кінетычная Wк;
б) патэнцыяльная Wп? Чаму яна роўна?
2. Матэматычны маятнік масай m = 100 г пры праходжанні становішча раўнавагі мае скорасць, модуль якой . Вызначыце:
а) поўную энергію Wмех маятніка;
б) максімальную вышыню hmax, на якую паднімаецца маятнік.
3. Матэматычны маятнік масай m = 100 г ввыводзяць са становішча раўнавагі, паднімаючы яго на вышыню h = 10 см над пачатковым узроўнем. Вызначыце:
а) измяненне патэнцыяльнай энергіі маятніка ΔWп пры яго адхіленні ад становішча раўнавагі;
б) яго максімальную кінетычную энергію (Wк)max.
4. Цела выконвае гарманічныя ваганні. Вызначыце адносіну кінетычнай энергіі да яе патэнцыяльнай энергіі для момантаў часу, калі зрух цела ад становішча раўнавагі роўны:
а) б)
в) x = A.
5. Груз масай m = 250 г ыконвае гарманічныя ваганні на спружыне жорсткасцю з амплітудай A = 3,6 см. Вызначыце поўную механічную энергію ваганняў W, патэнцыяльную Wп і кінетычную Wк энергіі ў момант часу, калі зрух грузу ад становішча раўнавагі х = 2,2 см. Патэнцыяльную энергію ў становішчы раўнавагі лічыць роўнай нулю.
6. Груз масай m = 100 г, які знаходзіцца на гладкай гарызантальнай паверхні, замацаваны на спружыне жорсткасцю прымацаванай да апоры. Яго зрушваюць са становішча раўнавагі на адлегласць х1 = 5,0 см і надаюць яму ў напрамку ад становішча раўнавагі скорасць, модуль якой
. Чаму роўны патэнцыяльная Wп і кінетычная Wк энергіі грузу ў гэты момант часу? Запішыце кінематычны закон яго руху.
7. Спружынны маятнік, які знаходзіцца на гладкай гарызантальнай паверхні, вывелі са становішча раўнавагі і без штуршка адпусцілі. Праз якую частку n перыяду Т кінетычная энергія прымацаванага да спружыны цела будзе роўна патэнцыяльнай энергіі Wп дэфармаванай спружыны?
8. Вызначыце поўную механічную энергію Wмех гарманічных ваганняў матэрыяльнага пункта, калі вядомы яго маса m, частата і амплітуда А ваганняў.
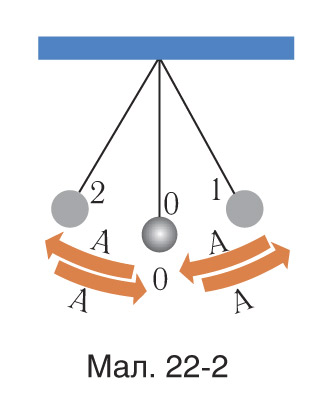
9. Запоўніце ў сшытку прыведзеную табліцу для ваганняў матэматычнага маятніка, паказанага на малюнку 22-2, калі маса шарыка , вышыня яго пад’ёму ад становішча раўнавагі
|
Становішча маятніка |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
10.Вызначыце амплітуду гарманічных ваганняў цела, калі поўная механічная энергія ваганняў , а максімальная сіла, якая дзейнічае на цела, —
.
11. Вертыкальны спружынны маятнік выконвае гарманічныя ваганні з амплітудай . Вызначыце зрушэнне
маятніка ад становішча раўнавагі ў пункце, у якім на яго дзейнічае вяртаючая сіла, модуль якой
, калі поўная механічная энергія маятніка
.
12.Матэрыяльны пункт масай выконвае гарманічныя ваганні з перыядам T і пачатковай фазай
. Максімальная кінетычная энергія пункта, што вагаецца, роўна
. Вызначыце амплітуду А ваганняў, модуль максімальнай скорасці
пункта і запішыце кінематычны закон яго руху
.
13.Куля масай m=10г, якая рухаецца гарызантальна са скорасцю, модуль якой , трапіла ў падвешаны на лёгкай нітцы драўляны шар масай m=1,0кг і захрасла ў ім. Пры гэтым нітка адхілілася ад вертыкалі на вугал
. Вызначыце перыяд T ваганняў шара.
14. Целу масай , падвешанаму на спружыне жорсткасцю
, у становішчы раўнавагі надаюць скорасць
, накіраваную вертыкальна ўніз. Вызначыце шлях, пройдзены целам за прамежак часу ад
да
, лічачы ваганні, што ўзніклі, гарманічнымі
15. Няхай перыяд ваганняў матэматычнага маятніка ў шахце глыбінёй роўны T. Вызначыце, на якую вышыню H над паверхняй Зямлі неабходна падняць гэты маятнік, каб перыяд яго ваганняў не змяніўся