§ 3. Ператварэнні энергіі пры гарманічных ваганнях
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 11 клас |
| Книга: | § 3. Ператварэнні энергіі пры гарманічных ваганнях |
| Напечатано:: | Гость |
| Дата: | Пятница, 4 Июль 2025, 11:43 |
|
Пры гарманічных ваганнях поўная механічная энергія сістэмы застаецца нязменнай, хоць скорасць грузу і яго зрух непарыўна змяняюцца з цягам часу. Якія ператварэнні энергіі назіраюцца ў сістэме пры гэтым? Як вылічыць кінетычную або патэнцыяльную энергію ў любы момант часу? |
Механічная энергія сістэмы роўна суме яе кінетычнай і патэнцыяльнай энергій. Кінетычнай энергіяй цела валодае з прычыны свайго руху, а патэнцыяльная энергія вызначаецца ўзаемадзеяннем цела з іншымі целамі ці сілавымі палямі. Механічная энергія замкнутай сістэмы, у якой не дзейнічаюць сілы трэння (супраціўлення), захоўваецца.
Прывесці ў рух вагальную сістэму можна або шляхам адхілення яе ад становішча раўнавагі, або надаваннем целу пачатковай скорасці (г. зн. пасродкам штуршка). У першым выпадку мы надаём сістэме дадатковую патэнцыяльную энергію, а ў другім — дадатковую кінетычную энергію.
Калі сілу трэння можна не ўлічваць, то пры ваганнях механічная энергія сістэмы захоўваецца. Пры гэтых умовах для дадзенай сістэмы выконваецца закон захавання механічнай энергіі:
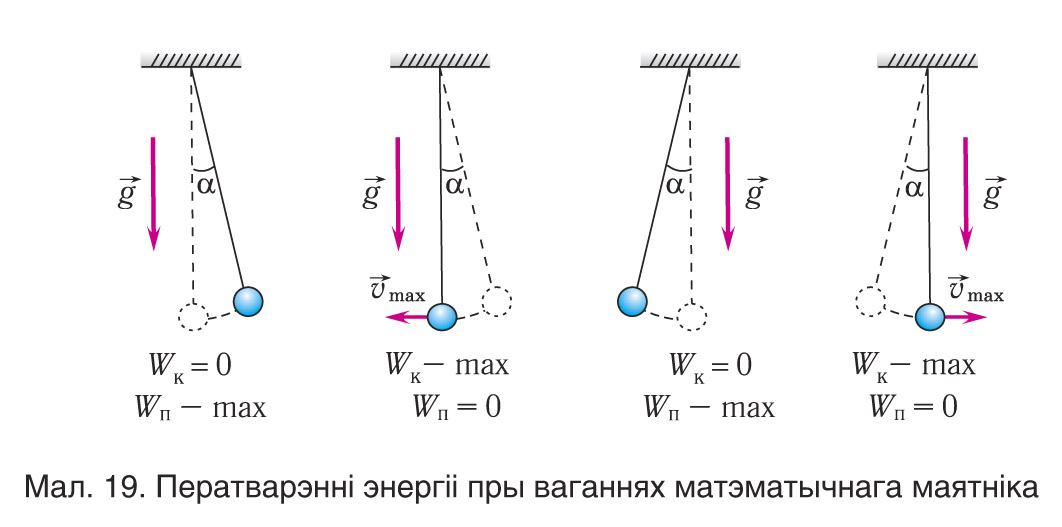
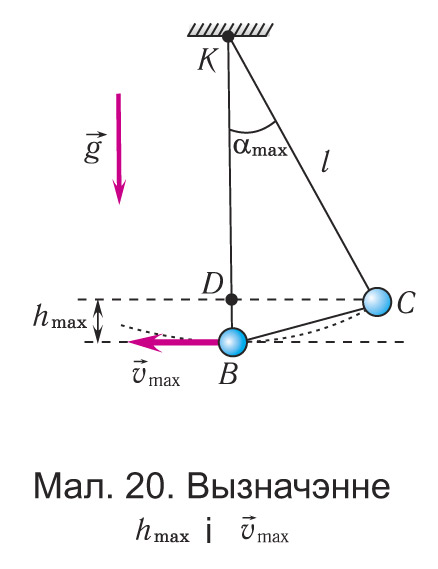
Разгледзім ператварэнні энергіі пры ваганнях матэматычнага маятніка. Выберам пачатак адліку патэнцыяльнай энергіі такім чынам, каб у становішчы раўнавагі яна была роўна нулю. Пры адхіленні маятніка на вугал (мал. 19, 20), які адпавядае яго максімальнаму зруху ад становішча раўнавагі (цела ў пункце С), патэнцыяльная энергія маятніка максімальная, а кінетычная энергія роўна нулю:
Паколькі ў момант праходжання становішча раўнавагі (цела ў пункце В) патэнцыяльная энергія маятніка роўна нулю Wп = 0, то з закону захавання механічнай энергіі вынікае (гл. мал. 20), што (Wк)В = (Wп)С, г. зн. што кінетычная энергія маятніка (а значыць, і скорасць) у гэты момант будзе максімальная:
Такім чынам, у становішчы раўнавагі патэнцыяльная энергія маятніка цалкам пераходзіць у кінетычную, а ў становішчах максімальнага адхілення — кінетычная энергія цалкам пераходзіць у патэнцыяльную. Прыраўнаваўшы поўныя механічныя энергіі маятніка ў пунктах С і В, атрымаем:
| (1) |
Адсюль знойдзем модуль максімальнай скорасці маятніка:
| (2) |
У любым прамежкавым становішчы
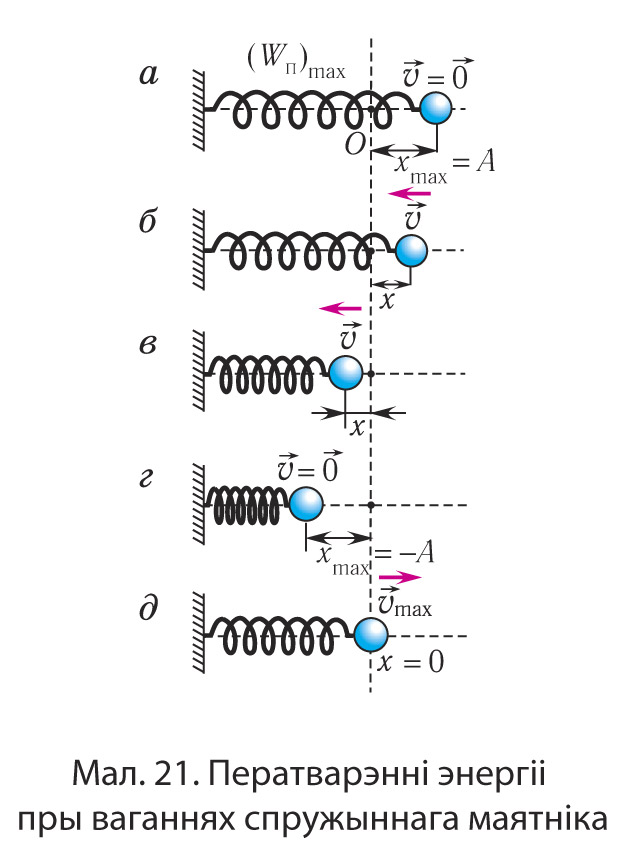
Пакажам, што аналагічныя ператварэнні энергіі маюць месца і для спружыннага маятніка (мал. 21).
У крайніх пунктах, калі x = ±A і скорасць маятніка v = 0, кінетычная энергія грузу цалкам пераходзіць у патэнцыяльную энергію дэфармаванай спружыны (гл. мал. 21, а, г)
|
|
Такім чынам, механічная энергія маятніка прапарцыянальна квадрату амплітуды яго ваганняў.
У становішчы раўнавагі, калі x = 0, уся энергія маятніка пераходзіць у кінетычную энергію грузу (гл. мал. 21, д):
|
|
дзе υmax — модуль максімальнай скорасці грузу пры ваганнях. У прамежкавых пунктах поўная энергія:
|
|
З улікам выразаў кінематычнага закону руху грузу и проекции скорости груза
, а таксама для
, знаходзім яго патэнцыяльную энергію
і кінетычную энергію:
у адвольны момант часу t .
Тады поўная механічная энергія спружыннага маятніка ў гэты ж момант часу ёсць велічыня пастаянная і роўная:
Такім чынам, пачатковае зрушэнне вызначае максімальную патэнцыяльную, а скорасць υmax вызначае максімальную кінетычную энергію цела, што вагаецца.
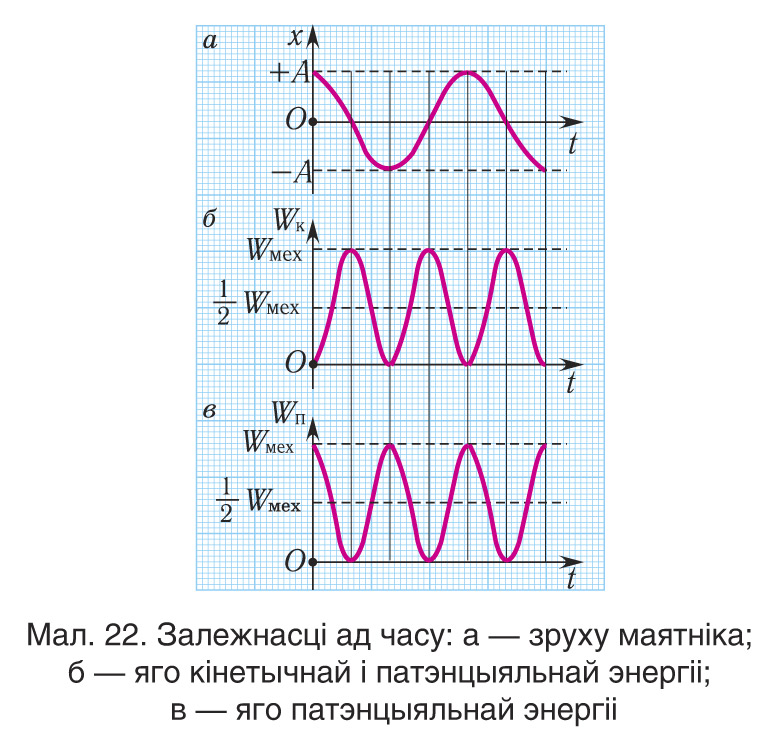
Пры адсутнасці ў сістэме страт энергіі працэс ваганняў суправаджаецца толькі пераходам патэнцыяльнай энергіі ў кінетычную і назад. Такія ператварэнні энергіі адбываюцца
з удвая большай частатой (мал. 22, а, б), чым самі ваганні. Сапраўды, двойчы за перыяд механічная энергія будзе цалкам ператварацца ў патэнцыяльную (у двух крайніх становішчах) і двойчы за перыяд — у кінетычную (пры праходжанні праз становішча раўнавагі) (мал. 22, в).
Пытаннi да параграфа
1. Якой энергіяй валодае матэматычны маятнік пры праходжанні становішча раўнавагі?
2. Якой энергіяй валодае спружынны маятнік пры найбольшым зруху ад становішча раўнавагі?
3. Чым адрозніваюцца патэнцыяльныя энергіі матэматычнага і спружыннага маятнікаў?
4. Як змяняецца энергія маятніка пры ваганнях?
5. Запішыце формулы для вызначэння механічнай энергіі цела, што вагаецца, пры праходжанні ім становішча раўнавагі і пры максімальным зруху з яго.
Прыклад рашэння задачы
1. Вызначыце поўную механічную энергію W ваганняў грузу масай m = 100 г на спружыне, калі ён выконвае гарманічныя ваганні з цыклічнай частатой і амплітудай А = 4,0 см.
m = 100 г = 0,10 кг
A=4,0 см=0,40 м
Рашэнне
Энергія ваганняў грузу:
дзе k — жорсткасць спружыны.
Паколькі цыклічная частата ваганняў грузу вызначаецца
, то
.
Канчаткова,
Адказ: W = 12 мДж.
1-1. Матэматычны маятнік пры ваганнях ад аднаго крайняга становішча да другога зрушваецца на адлегласць і пры праходжанні становішча раўнавагі дасягае скорасці, модуль якой
. Вызначыце перыяд T ваганняў маятніка.
Рашэнне
Па законе захавання механічнай энергіі
Адкуль
Адказ:
1-2. Груз масай знаходзіцца на гладкай гарызантальнай паверхні і прымацаваны да апоры на лёгкай спружыне жорсткасцю
. Яго зрушваюць на адлегласць х = 3,00 см ад становішча раўнавагі і надаюць у напрамку ад становішча раўнавагі скорасць, модуль якой
. Вызначыце патэнцыяльную
і кінетычную энергію
грузу ў пачатковы момант часу. Запішыце кінематычны закон руху грузу
.
Рашэнне
Патэнцыяльная энергія грузу вызначаецца выразам
,
Кінетычная энергія грузу вызначаецца выразам
,
Пачатковае зрушэнне грузу не з’яўляецца амплітудай, паколькі разам з пачатковым адхіленнем грузу надалі і скорасць. Аднак поўная энергія можа быць выражана праз амплітуду ваганняў
Адкуль
Цыклічная частата
У пачатковы момант часу каардыната грузу
.
Адкуль пачатковая фаза
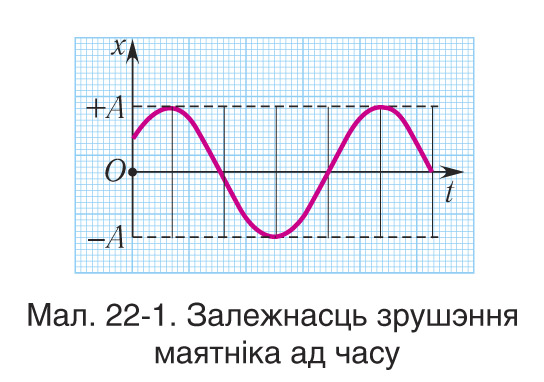
Тады закон гарманічных ваганняў мае выгляд (мал. 22-1):
Адказ: ,
,
Практыкаванне 3
1. У якіх пунктах траекторыі пры ваганнях матэматычнага маятніка максімальная энергія:
а) кінетычная Wк;
б) патэнцыяльная Wп? Чаму яна роўна?
2. Матэматычны маятнік масай m = 100 г пры праходжанні становішча раўнавагі мае скорасць, модуль якой . Вызначыце:
а) поўную энергію Wмех маятніка;
б) максімальную вышыню hmax, на якую паднімаецца маятнік.
3. Матэматычны маятнік масай m = 100 г ввыводзяць са становішча раўнавагі, паднімаючы яго на вышыню h = 10 см над пачатковым узроўнем. Вызначыце:
а) измяненне патэнцыяльнай энергіі маятніка ΔWп пры яго адхіленні ад становішча раўнавагі;
б) яго максімальную кінетычную энергію (Wк)max.
4. Цела выконвае гарманічныя ваганні. Вызначыце адносіну кінетычнай энергіі да яе патэнцыяльнай энергіі для момантаў часу, калі зрух цела ад становішча раўнавагі роўны:
а) б)
в) x = A.
5. Груз масай m = 250 г ыконвае гарманічныя ваганні на спружыне жорсткасцю з амплітудай A = 3,6 см. Вызначыце поўную механічную энергію ваганняў W, патэнцыяльную Wп і кінетычную Wк энергіі ў момант часу, калі зрух грузу ад становішча раўнавагі х = 2,2 см. Патэнцыяльную энергію ў становішчы раўнавагі лічыць роўнай нулю.
6. Груз масай m = 100 г, які знаходзіцца на гладкай гарызантальнай паверхні, замацаваны на спружыне жорсткасцю прымацаванай да апоры. Яго зрушваюць са становішча раўнавагі на адлегласць х1 = 5,0 см і надаюць яму ў напрамку ад становішча раўнавагі скорасць, модуль якой
. Чаму роўны патэнцыяльная Wп і кінетычная Wк энергіі грузу ў гэты момант часу? Запішыце кінематычны закон яго руху.
7. Спружынны маятнік, які знаходзіцца на гладкай гарызантальнай паверхні, вывелі са становішча раўнавагі і без штуршка адпусцілі. Праз якую частку n перыяду Т кінетычная энергія прымацаванага да спружыны цела будзе роўна патэнцыяльнай энергіі Wп дэфармаванай спружыны?
8. Вызначыце поўную механічную энергію Wмех гарманічных ваганняў матэрыяльнага пункта, калі вядомы яго маса m, частата і амплітуда А ваганняў.
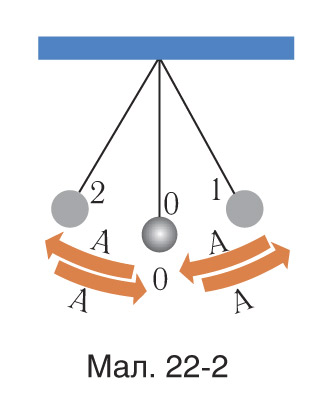
9. Запоўніце ў сшытку прыведзеную табліцу для ваганняў матэматычнага маятніка, паказанага на малюнку 22-2, калі маса шарыка , вышыня яго пад’ёму ад становішча раўнавагі
|
Становішча маятніка |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
10.Вызначыце амплітуду гарманічных ваганняў цела, калі поўная механічная энергія ваганняў , а максімальная сіла, якая дзейнічае на цела, —
.
11. Вертыкальны спружынны маятнік выконвае гарманічныя ваганні з амплітудай . Вызначыце зрушэнне
маятніка ад становішча раўнавагі ў пункце, у якім на яго дзейнічае вяртаючая сіла, модуль якой
, калі поўная механічная энергія маятніка
.
12.Матэрыяльны пункт масай выконвае гарманічныя ваганні з перыядам T і пачатковай фазай
. Максімальная кінетычная энергія пункта, што вагаецца, роўна
. Вызначыце амплітуду А ваганняў, модуль максімальнай скорасці
пункта і запішыце кінематычны закон яго руху
.
13.Куля масай m=10г, якая рухаецца гарызантальна са скорасцю, модуль якой , трапіла ў падвешаны на лёгкай нітцы драўляны шар масай m=1,0кг і захрасла ў ім. Пры гэтым нітка адхілілася ад вертыкалі на вугал
. Вызначыце перыяд T ваганняў шара.
14. Целу масай , падвешанаму на спружыне жорсткасцю
, у становішчы раўнавагі надаюць скорасць
, накіраваную вертыкальна ўніз. Вызначыце шлях, пройдзены целам за прамежак часу ад
да
, лічачы ваганні, што ўзніклі, гарманічнымі
15. Няхай перыяд ваганняў матэматычнага маятніка ў шахце глыбінёй роўны T. Вызначыце, на якую вышыню H над паверхняй Зямлі неабходна падняць гэты маятнік, каб перыяд яго ваганняў не змяніўся