§ 3. Ператварэнні энергіі пры гарманічных ваганнях
|
Пры гарманічных ваганнях поўная механічная энергія сістэмы застаецца нязменнай, хоць скорасць грузу і яго зрух непарыўна змяняюцца з цягам часу. Якія ператварэнні энергіі назіраюцца ў сістэме пры гэтым? Як вылічыць кінетычную або патэнцыяльную энергію ў любы момант часу? |
Механічная энергія сістэмы роўна суме яе кінетычнай і патэнцыяльнай энергій. Кінетычнай энергіяй цела валодае з прычыны свайго руху, а патэнцыяльная энергія вызначаецца ўзаемадзеяннем цела з іншымі целамі ці сілавымі палямі. Механічная энергія замкнутай сістэмы, у якой не дзейнічаюць сілы трэння (супраціўлення), захоўваецца.
Прывесці ў рух вагальную сістэму можна або шляхам адхілення яе ад становішча раўнавагі, або надаваннем целу пачатковай скорасці (г. зн. пасродкам штуршка). У першым выпадку мы надаём сістэме дадатковую патэнцыяльную энергію, а ў другім — дадатковую кінетычную энергію.
Калі сілу трэння можна не ўлічваць, то пры ваганнях механічная энергія сістэмы захоўваецца. Пры гэтых умовах для дадзенай сістэмы выконваецца закон захавання механічнай энергіі:
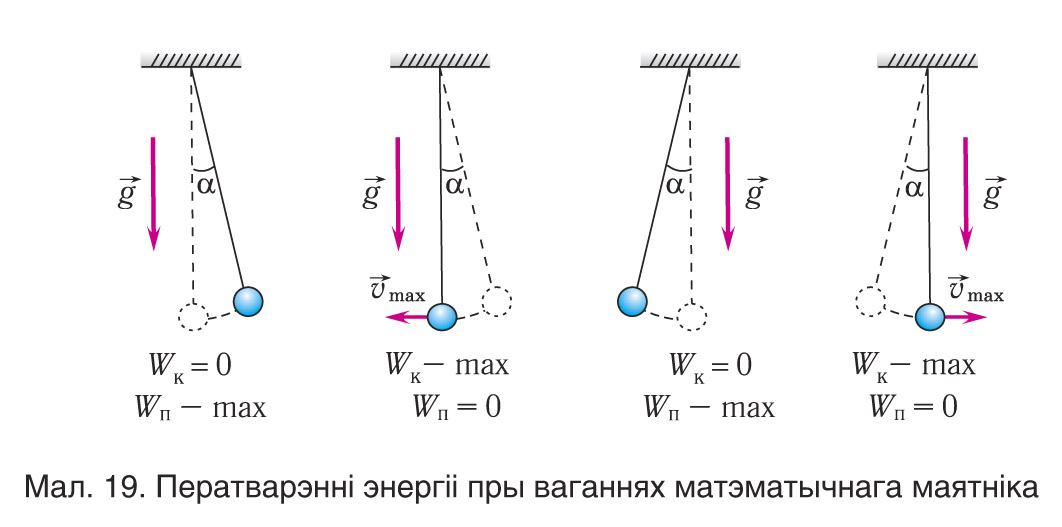
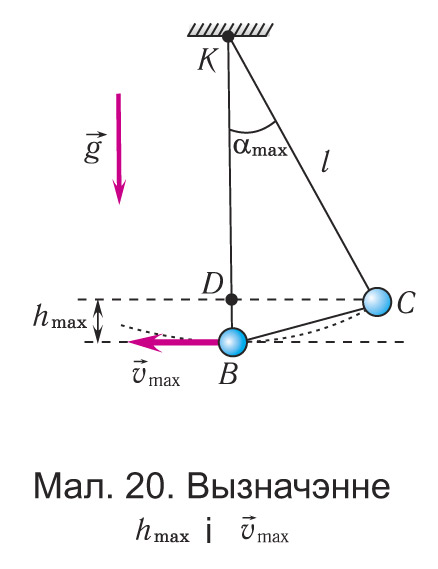
Разгледзім ператварэнні энергіі пры ваганнях матэматычнага маятніка. Выберам пачатак адліку патэнцыяльнай энергіі такім чынам, каб у становішчы раўнавагі яна была роўна нулю. Пры адхіленні маятніка на вугал (мал. 19, 20), які адпавядае яго максімальнаму зруху ад становішча раўнавагі (цела ў пункце С), патэнцыяльная энергія маятніка максімальная, а кінетычная энергія роўна нулю:
Паколькі ў момант праходжання становішча раўнавагі (цела ў пункце В) патэнцыяльная энергія маятніка роўна нулю Wп = 0, то з закону захавання механічнай энергіі вынікае (гл. мал. 20), што (Wк)В = (Wп)С, г. зн. што кінетычная энергія маятніка (а значыць, і скорасць) у гэты момант будзе максімальная:
Такім чынам, у становішчы раўнавагі патэнцыяльная энергія маятніка цалкам пераходзіць у кінетычную, а ў становішчах максімальнага адхілення — кінетычная энергія цалкам пераходзіць у патэнцыяльную. Прыраўнаваўшы поўныя механічныя энергіі маятніка ў пунктах С і В, атрымаем:
| (1) |
Адсюль знойдзем модуль максімальнай скорасці маятніка:
| (2) |
У любым прамежкавым становішчы
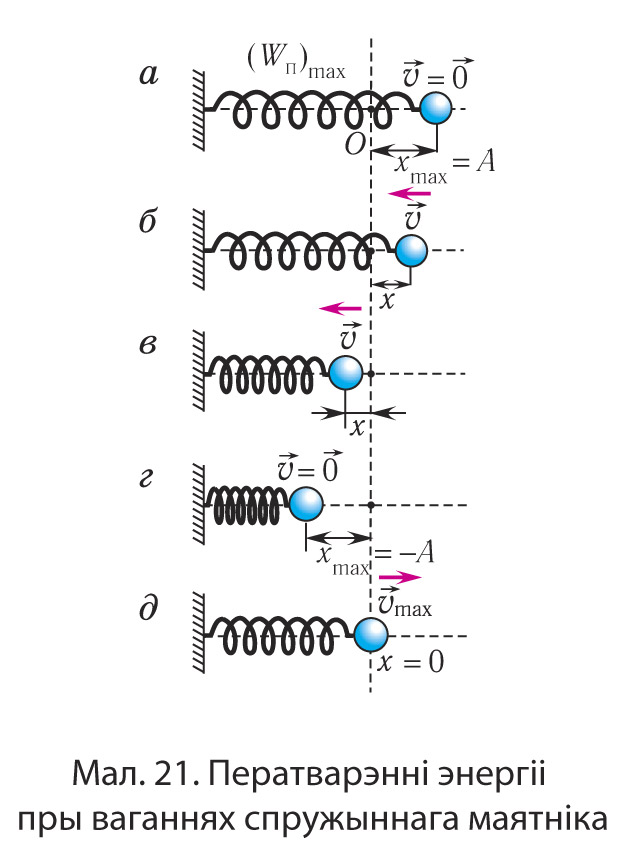
Пакажам, што аналагічныя ператварэнні энергіі маюць месца і для спружыннага маятніка (мал. 21).
У крайніх пунктах, калі x = ±A і скорасць маятніка v = 0, кінетычная энергія грузу цалкам пераходзіць у патэнцыяльную энергію дэфармаванай спружыны (гл. мал. 21, а, г)
|
|
Такім чынам, механічная энергія маятніка прапарцыянальна квадрату амплітуды яго ваганняў.
У становішчы раўнавагі, калі x = 0, уся энергія маятніка пераходзіць у кінетычную энергію грузу (гл. мал. 21, д):
|
|
дзе υmax — модуль максімальнай скорасці грузу пры ваганнях. У прамежкавых пунктах поўная энергія:
|
|
З улікам выразаў кінематычнага закону руху грузу и проекции скорости груза
, а таксама для
, знаходзім яго патэнцыяльную энергію
і кінетычную энергію:
у адвольны момант часу t .
Тады поўная механічная энергія спружыннага маятніка ў гэты ж момант часу ёсць велічыня пастаянная і роўная:
Такім чынам, пачатковае зрушэнне вызначае максімальную патэнцыяльную, а скорасць υmax вызначае максімальную кінетычную энергію цела, што вагаецца.
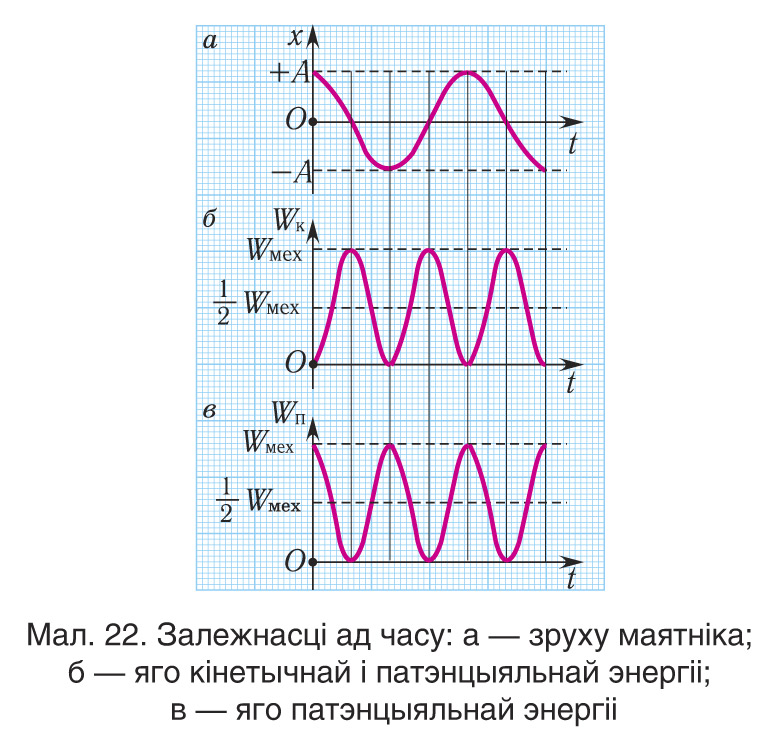
Пры адсутнасці ў сістэме страт энергіі працэс ваганняў суправаджаецца толькі пераходам патэнцыяльнай энергіі ў кінетычную і назад. Такія ператварэнні энергіі адбываюцца
з удвая большай частатой (мал. 22, а, б), чым самі ваганні. Сапраўды, двойчы за перыяд механічная энергія будзе цалкам ператварацца ў патэнцыяльную (у двух крайніх становішчах) і двойчы за перыяд — у кінетычную (пры праходжанні праз становішча раўнавагі) (мал. 22, в).