§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле
Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?
Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца (1853–1928).
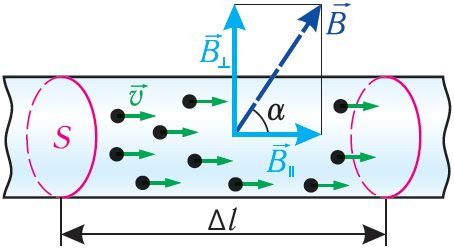
Модуль силы Лоренца можно определить по формуле «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«msub»«mi»F«/mi»«mi mathvariant=¨normal¨»§#1051;«/mi»«/msub»«mo»=«/mo»«mfrac»«msub»«mi»F«/mi»«mi mathvariant=¨normal¨»§#1040;«/mi»«/msub»«mi»N«/mi»«/mfrac»«/mrow»«/mstyle»«/math» , где N — общее число свободных заряженных одинаковых частиц на прямолинейном участке проводника длиной Δl (рис. 167). Если модуль заряда одной частицы q, а модуль суммарного заряда всех частиц Nq, то согласно определению силы тока «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«mi»I«/mi»«mo»=«/mo»«mfrac»«mrow»«mi»N«/mi»«mi»q«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math», где Δt — промежуток времени, за который заряженная частица проходит участок проводника длиной Δl. Тогда
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«msub»«mi»F«/mi»«mi mathvariant=¨normal¨»§#1051;«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«mi»B«/mi»«mi»I«/mi»«mo»§#8710;«/mo»«mi»l«/mi»«mo»§#160;«/mo»«mi»sin§#945;«/mi»«/mrow»«mi»N«/mi»«/mfrac»«mo»=«/mo»«mfrac»«mrow»«mi»B«/mi»«mi»N«/mi»«mi»q«/mi»«mo»§#8710;«/mo»«mi»l«/mi»«mo»§#160;«/mo»«mi»sin§#945;«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«mi»N«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mfrac»«mrow»«mi»B«/mi»«mi»q«/mi»«mo»§#8710;«/mo»«mi»l«/mi»«mo»§#160;«/mo»«mi»sin§#945;«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«mo».«/mo»«/mrow»«/mstyle»«/math»
Поскольку «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«mfrac»«mrow»«mo»§#8710;«/mo»«mi»l«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mi»§#965;«/mi»«/mrow»«/mstyle»«/math» – модуль средней скорости упорядоченного движения заряженной частицы в стационарном* электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«msub»«mi»F«/mi»«mi mathvariant=¨normal¨»§#1051;«/mi»«/msub»«mo»=«/mo»«mi»B«/mi»«mi»q«/mi»«mi»§#965;«/mi»«mo»§#160;«/mo»«mi»sin§#945;«/mi»«mo»,«/mo»«/mrow»«/mstyle»«/math»
(30.1)
где α — угол между направлениями индукции магнитного поля «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover»«mi»B«/mi»«mo»§#8594;«/mo»«/mover»«/mstyle»«/math» и скорости «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover»«mi»§#965;«/mi»«mo»§#8594;«/mo»«/mover»«/mstyle»«/math» упорядоченного движения заряженной частицы.
Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.
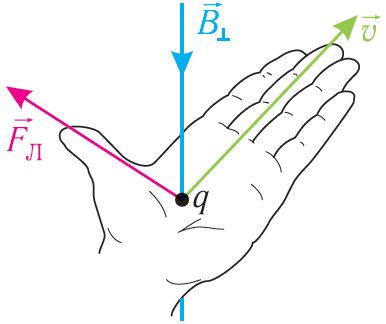
Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.
Сила Лоренца перпендикулярна как направлению скорости «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover»«mi»§#965;«/mi»«mo»§#8594;«/mo»«/mover»«/mstyle»«/math» движения частицы, так и направлению индукции «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover»«mi»B«/mi»«mo»§#8594;«/mo»«/mover»«/mstyle»«/math» магнитного поля.
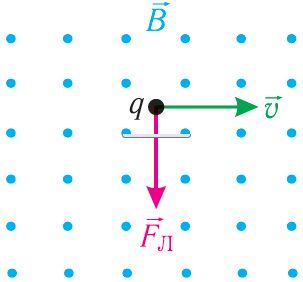
На рисунке 169 представлены направления индукции «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover»«mi»B«/mi»«mo»§#8594;«/mo»«/mover»«/mstyle»«/math» магнитного поля, скорости «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover»«mi»§#965;«/mi»«mo»§#8594;«/mo»«/mover»«/mstyle»«/math» движения частицы в данный момент времени и силы Лоренца «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1051;«/mi»«/msub»«/mstyle»«/math», действующей на частицу со стороны магнитного поля. Определите знак заряда частицы.
* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑