Физика. 10 класс

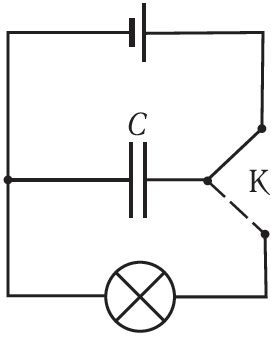
Убедиться в том, что заряженный конденсатор обладает энергией, можно на опыте. Соберём электрическую цепь, состоящую из источника тока, конденсатора и электрической лампы. Схема цепи представлена на рисунке 125. Зарядим конденсатор, подсоединив его к источнику тока. Затем, отключив конденсатор от источника тока, подсоединим его к лампе. При этом наблюдаем кратковременную вспышку света. В данном случае во время разрядки конденсатора энергия, запасённая им при зарядке, превращается во внутреннюю энергию спирали лампы, часть этой энергии расходуется на излучение света. При прохождении электрического тока по цепи с источником тока конденсатор заряжался, т. е. на его обкладках накапливались электрические заряды. При этом в окружающем конденсатор пространстве возникло электростатическое поле. Суммарный электрический заряд обеих обкладок конденсатора до его зарядки, во время зарядки и после разрядки конденсатора равен нулю. Единственное изменение, которое произошло при разрядке конденсатора, заключается в том, что исчезло электростатическое поле, которое создавалось зарядами обеих обкладок конденсатора. Следовательно, энергией обладало электростатическое поле, образованное зарядами обкладок заряженного конденсатора.

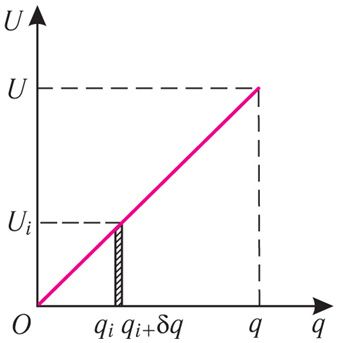
Если форма и размеры обкладок конденсатора, а также расстояние между ними и диэлектрические свойства среды, заполняющей пространство между обкладками, остаются неизменными, то напряжение на конденсаторе прямо пропорционально модулю заряда его обкладок «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»U«/mi»«mo»=«/mo»«mfrac»«mn»1«/mn»«mi»C«/mi»«/mfrac»«mi»q«/mi»«/math» (рис. 125.1). Чтобы увеличить модуль заряда на обкладках от q_i до q_i + δq, внешней силе необходимо совершить работу «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨normal¨»§#948;«/mi»«msubsup»«mi»A«/mi»«mi»i«/mi»«mi»§#1074;§#1085;§#1077;§#1096;«/mi»«/msubsup»«mo»=«/mo»«msub»«mi»U«/mi»«mi»i«/mi»«/msub»«mo»§#183;«/mo»«mi mathvariant=¨normal¨»§#948;«/mi»«mi»q«/mi»«/math» по перемещению бесконечно малой положительной порции заряда δq с отрицательной обкладки на положительную. Этой работе на рисунке 125.1 соответствует площадь заштрихованного столбика. Полная же работа А_внеш по зарядке конденсатора до напряжения U равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости U(q). В данном случае — площади треугольника, равной половине произведения его основания на высоту:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»A«/mi»«mi»§#1074;§#1085;§#1077;§#1096;«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«mi»q«/mi»«mi»U«/mi»«/mrow»«mn»2«/mn»«/mfrac»«mo».«/mo»«/math»