§ 12. Работа в термодинамике
В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.
Работа в термодинамике. Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.
Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.
Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.
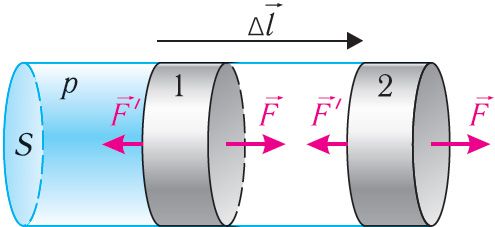
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре р. В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние Δl. Модуль силы давления газа на поршень F = pS. Эта сила совершила работу по перемещению поршня, равную
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»A«/mi»«mn»12«/mn»«/msub»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mi»F«/mi»«mi mathvariant=¨normal¨»§#916;«/mi»«mi»l«/mi»«mi»cos§#945;«/mi»«/math»,
где «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»§#945;«/mi»«/math» — угол между направлениями силы «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«/math» и перемещения поршня «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«mover»«mi»l«/mi»«mo»§#8594;«/mo»«/mover»«/math».
Поскольку в рассматриваемом примере α = 0 и cosα = 1, то
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»A«/mi»«mn»12«/mn»«/msub»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mi»p«/mi»«mi»S«/mi»«mi mathvariant=¨normal¨»§#916;«/mi»«mi»l«/mi»«/math».
Произведение SΔl определяет изменение объёма ∆V = V2 – V1, где V1 — начальный объём газа; V2 — объём газа в конечном состоянии (см. рис. 66).
Таким образом, работа силы давления газа при его изобарном расширении:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»A«/mi»«mn»12«/mn»«/msub»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mi»p«/mi»«mi mathvariant=¨normal¨»§#916;«/mi»«mi»V«/mi»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mi»p«/mi»«mo»(«/mo»«msub»«mi»V«/mi»«mn»2«/mn»«/msub»«mo»§#8211;«/mo»«msub»«mi»V«/mi»«mn»1«/mn»«/msub»«mo»)«/mo»«/math».
(12.1)
Так как давление р газа — величина положительная, то из формулы (12.1) следует, что A12 > 0.
При изобарном расширении газа из состояния 1 в состояние 2 работа силы «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mo»`«/mo»«/math» (см. рис. 66):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»A«/mi»«msub»«mo»`«/mo»«mn»12«/mn»«/msub»«mo»=«/mo»«mo»§#160;«/mo»«mi»F«/mi»«mo»`«/mo»«mi mathvariant=¨normal¨»§#916;«/mi»«mi»l«/mi»«mi»cos§#946;«/mi»«/math»,
где «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»F«/mi»«mo»`«/mo»«/math» — модуль силы, действующей на газ со стороны поршня (внешняя сила); «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»§#946;«/mi»«/math» — угол между направлениями силы «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mrow»«mi»F«/mi»«mo»`«/mo»«/mrow»«mo»§#8594;«/mo»«/mover»«/math» и перемещения «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«mover»«mi»l«/mi»«mo»§#8594;«/mo»«/mover»«/math» поршня.
Перемещение «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«mover»«mi»l«/mi»«mo»§#8594;«/mo»«/mover»«/math» поршня одно и то же, а сила давления «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«/math» газа на поршень и сила давления «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mrow»«mi»F«/mi»«mo»`«/mo»«/mrow»«mo»§#8594;«/mo»«/mover»«/math» поршня на газ — силы, подчиняющиеся третьему закону Ньютона:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mo»-«/mo»«mover»«mrow»«mi»F«/mi»«mo»`«/mo»«/mrow»«mo»§#8594;«/mo»«/mover»«/math».
Следовательно, работы «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»A«/mi»«msub»«mo»`«/mo»«mn»12«/mn»«/msub»«/math» и «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»A«/mi»«mn»12«/mn»«/msub»«/math» отличаются только знаком («math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»cos§#946;«/mi»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mi»cos«/mi»«mn»180«/mn»«mo»§#176;«/mo»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mo»-«/mo»«mn»1«/mn»«/math»):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»A«/mi»«msub»«mo»`«/mo»«mn»12«/mn»«/msub»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mo»-«/mo»«msub»«mi»A«/mi»«mn»12«/mn»«/msub»«mo»§#160;«/mo»«mo»=«/mo»«mo»§#160;«/mo»«mo»-«/mo»«mi»p«/mi»«mo»§#8710;«/mo»«mi»V«/mi»«/math».
Таким образом, можно сделать следующие выводы.
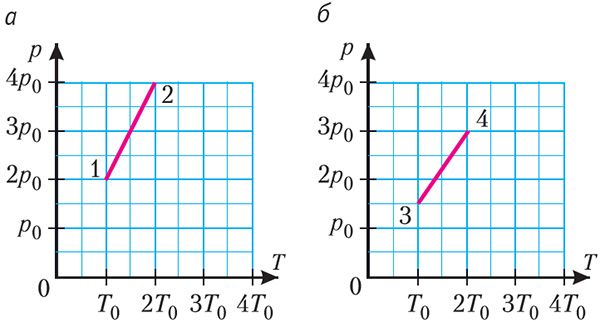
На рисунке 67, а представлен процесс перехода идеального газа определённой массы из состояния 1 в состояние 2, а на рисунке 67, б — процесс перехода этого же газа из состояния 3 в состояние 4. Сравните работы, совершённые силой давления газа в обоих процессах, и изменения значений его внутренней энергии.