Математика 11 класс (IT-практикум)

• Онлайн-сервис Google сайты
• математическая среда GeoGebra

Используя учебный материал §7 учебного пособия «Геометрия. 11 класс», а также ресурсы сети Интернет, соберите информацию для наполнения информационной страницы «Правильные многогранники».

На странице сайта должна быть изложена следующая информация:
   – определение правильных многогранников; какие геометрические тела к ним относятся; каковы их параметры; почему их называют платоновыми телами;
   – изображения правильных многогранников (3D-модели);
   – из каких плоских фигур состоит каждый правильный многогранник;
   – каковы свойства правильных многогранников. 

Примечание. Рекомендуется ознакомиться с информацией в статье «Динамическая математическая программа GeoGebra».

Разместите собранную вами информацию на странице сайта, используйте для вставки информации блоки с панели «Вставка».

Например, информацию о параметрах правильных многогранников можно разместить в виде списка или таблицы: название многогранника, число его вершин, ребер, граней, число сторон у граней и число ребер, примыкающих к одной вершине.

Также можно добавить информацию о каждом правильном многограннике: почему он так называется и из каких фигур он состоит. 

Для добавления изображений (3D-моделей) правильных многогранников используйте инструментарий математической среды GeoGebra.

Перейдите по ссылке GeoGebra.

Для построения тетраэдра нажмите кнопку  и выберите команду .
Далее задайте на плоскости основания две точки – длину ребра. 
Тетраэдр построен (посмотреть модель).

 Примечание. Также можно воспользоваться установленной на компьютер программой GeoGebra Classic 6 (  – команда «Перспективы» – 3D графика);
   – зарегистрируйтесь или войдите с помощью учетной записи Google – это нужно для сохранения результатов ваших построений и перехода на русскоязычный интерфейс приложения: кнопка   (правый верхний угол) – команда  («Войти»); выберите вариант Google.

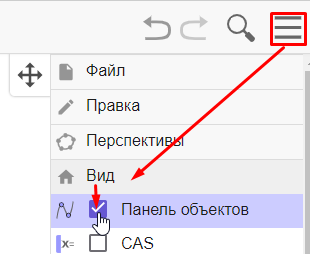
Скройте лишние элементы на чертеже:

   – систему координат: нажмите в правом верхнем углу кнопку  (панель параметров объектов), выберите команду «Оси» и один из понравившихся режимов отображения.  

   – панель объектов: нажмите в правом верхнем углу кнопку   , выберите команду «Вид» и уберите галочку напротив фразы «Панель объектов».

Примечание. После выполнения построения определенным инструментом его надо выключать, чтобы не «засорять» чертеж ненужными объектами.
Выключение инструмента можно выполнить нажатием кнопки Esc на клавиатуре или выбором инструмента .

Сохраните свой чертеж с названием «Тетраэдр»:  –  .
Скопируйте ссылку на чертеж для публикации на сайте ( – ).

Встройте ваш чертеж на информационную страницу «Правильные многогранники» сайта «Математика с компьютером» (вкладка «Вставка» – «Встроить» – Встроить URL).

Примечание. Можно сначала сохранить свой чертеж на компьютере, а потом загрузить его в свой аккаунт на сайте GeoGebra.org. 

Для построения гексаэдра на новом чертеже (  – Файл – Создать) нажмите кнопку  и выберите команду .

Далее задайте на плоскости основания две точки – длину ребра. 
Гексаэдр (куб) построен. 

Повторите п. 5 для данного чертежа (название модели «Гексаэдр или куб»).

Для построения октаэдра на новом чертеже (  – Файл – Создать) задайте на плоскости основания две точки – длину ребра.
Далее в строке «Ввод» на панели объектов добавьте «Октаэдр[A, B]» и нажмите ввод. 

Примечание. A, B – это точки на плоскости основания, которые задали длину ребра. 
Октаэдр построен. 

Повторите п. 5 для данного чертежа (название модели «Октаэдр»).

Для построения додекаэдра на новом чертеже (  – Файл – Создать) задайте на плоскости основания две точки – длину ребра.
Далее в строке «Ввод» на панели объектов добавьте «Додекаэдр[A, B]» и нажмите ввод. 

Примечание. A, B – это точки на плоскости основания, которые задали длину ребра. 
Додекаэдр построен (посмотреть). 

Повторите п. 5 для данного чертежа (название модели «Додекаэдр»).

Для построения икосаэдра на новом чертеже (  – Файл – Создать) задайте на плоскости основания две точки – длину ребра.
Далее в строке «Ввод» на панели объектов добавьте «Икосаэдр[A, B]» и нажмите ввод. 

Примечание. A, B – это точки на плоскости основания, которые задали длину ребра. 
Икосаэдр построен. 

Повторите п. 5 для данного чертежа (название модели «Икосаэдр»).

Для доступа пользователей к новым материалам сайта нажмите кнопку «Опубликовать».

Учитель математики может использовать информационную страницу «Правильные многогранники» в образовательном процессе.

1. Видео «GeoGebra за 19 минут»