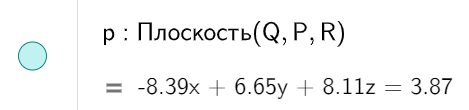Математика 11 класс (IT-практикум)

Опишем последовательность действий в программе для выполнения чертежа:

   –  Построение основания призмы – произвольного треугольника.
   –  Построение прямой, содержащей ребро АА₁.
   –  Построение призмы.
   –  Построение точек, определяющих секущую плоскость.
   –  Построение секущей плоскости.
   –  Выделение многоугольника, являющегося сечением призмы.

Примечание. Рекомендуется ознакомиться с информацией в статье «Динамическая математическая программа GeoGebra».

Для организации работы с заданием выполните следующие действия:

   – перейдите по ссылке на сайт GeoGebra.
   Также можно воспользоваться установленной на компьютер программой GeoGebra Classic 6 (  – команда «Перспективы» – 3D графика);
   – зарегистрируйтесь или войдите с помощью учетной записи Google – это нужно для сохранения результатов ваших построений и перехода на русскоязычный интерфейс приложения: кнопка   (правый верхний угол) - команда  («Войти»); выберите вариант Google.

Примечание. Переключение интерфейса программы на русский язык обычно происходит после авторизации.
Если это не произошло, нажмите: кнопка    (правый верхний угол) – команда  ( Настройки) – , в выпадающем меню выберите вариант «Русский» – Сохранить изменения. 

В плоскости основания постройте произвольный треугольник: на панели инструментов нажмите кнопку   и выберите команду  (последовательно выполните щелчки на месте нахождения вершин треугольника, последний щелчок делается снова на первую вершину треугольника).

Примечание. После выполнения построения определенным инструментом построения его надо отключать, чтобы не «засорять» чертеж ненужными объектами.

Отключение инструмента можно выполнить нажатием кнопки Esc на клавиатуре или выбором инструмента.

Для построения призмы необходимо определить положение любой вершины верхнего основания. 

Примечание. Согласно особенностям работы в программе GeoGebra, произвольно построить точку в пространстве нельзя – она должна принадлежать какому-то геометрическому объекту.

Постройте прямую, содержащую ребро АА₁.
Так как данное ребро перпендикулярно плоскости основания, то для его построения нажмите кнопку   и выберите команду  (последовательно нажмите на точку А и плоскость основания).

Примечание. Не забывайте отключать режим инструментов для построения (кнопка Esc на клавиатуре). 

Для построения призмы нажмите кнопку    и выберите команду .
Выполните щелчок мыши по треугольнику основания и «вытяните» его вдоль прямой, проходящей через точку А, на высоту призмы.
Призма построена.

По условию задачи призма имеет название ABCA₁B₁C₁.
Переименуйте вершину верхнего основания на А₁ (прямая АF). 
Для изменения имени точки выполните на ней щелчок, наберите с клавиатуры новое имя A₁ и нажмите Enter.
Через пару секунд название поменяется на выбранное.

Поменяйте остальные имена вершин верхнего основания.

Примечание. Имена геометрических объектов в программе набираются буквами латинского алфавита. 

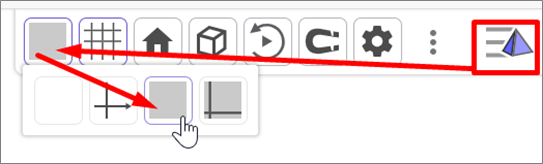
Для установки на чертеже точек, которые определяют сечение, нажмите кнопку  и выберите команду .

Установите точки и переименуйте их в соответствии с условием задачи. 

Примечание. Скройте координатные оси и прямую АА₁.
Для этого нажмите в правом верхнем углу кнопку  (панель параметров объектов), выберите команду «Оси» и один из понравившихся режимов отображения. 

Чтобы скрыть прямую АА₁, найдите ее описание на панели объектов слева и выполните щелчок на цветовом круге возле описания.

Для построения секущей плоскости нажмите кнопку , выберите команду  и нажмите поочередно на точки Р, Q и R.
Построена секущая плоскость.
Примечание. Не забывайте отключать режим инструментов для построения (кнопка Esc на клавиатуре).

Рассмотрите внимательно ваш чертеж и ответьте на вопросы:
В каких точках плоскость пересекает ребра призмы?
Какая фигура получилась в сечении?

Примечание. Для изменения статического положения построенного чертежа в пространстве нужно нажать левую кнопку мыши и выполнить движение в сторону по или против часовой стрелке (вращение чертежа).

Для выделения многоугольника, являющегося сечением призмы, выберите команду   , подведите курсор к линии, которая определяет сечение внутри призмы.
Как только линия появится – выполните по ней щелчок.

Сечение построено. 
Интерактивный чертеж к заданию (clck.ru/3ExeNw)

Примечание. На предложенном автором интерактивном чертеже внизу окна есть инструмент, позволяющий посмотреть этапы построения чертежа.  

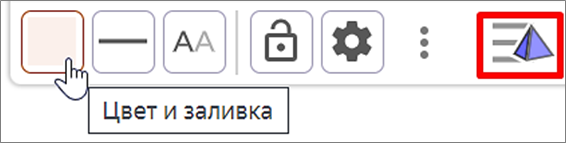
Теперь можно скрыть секущую плоскость и увеличить интенсивность заливки многоугольника, который является сечением призмы.

Для того чтобы скрыть секущую плоскость, найдите описание плоскости на панели объектов слева и выполните щелчок на цветовом круге возле описания.

Для изменения цвета заливки призмы, линий и точек нажмите в правом верхнем углу кнопку  (панель параметров объектов) и выберите команду «Цвет и заливка».
Уменьшите интенсивность / измените цвет заливки сечения.

Измените положение точек, определяющих плоскость сечения. 
Посмотрите, как будет изменяться внешний вид сечения.

Ответьте на вопрос: Какие фигуры получаются в сечении призмы плоскостью?

Сохраните свой чертеж с названием «Сечение прямой призмы плоскостью»:  – .
Скопируйте ссылку на чертеж для публикации на сайте ( – ).

Разместите ссылку на интерактивный чертеж на сайте «Математика с компьютером».

Для этого:
   – перейдите по ссылке sites.google.com и выберите ваш сайт;
   – откроется редактор сайта.
   Перейдите на страницу «Многогранники».
   На вкладке «Вставка» выберите блок «Текст» и добавьте название вашей интерактивной модели.
   Далее выберите блок «Встроить» и добавьте ссылку из буфера памяти на вашу модель;
   – для доступа пользователей к новым материалам на сайте нажмите кнопку «Опубликовать».

Учитель математики может использовать интерактивную модель «Сечение прямой призмы плоскостью» при изучении темы «Призма».

Посмотреть модель. 

1. Видео «GeoGebra за 19 минут»