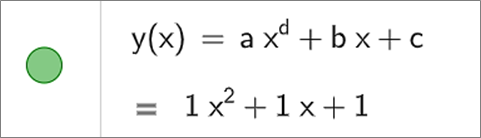ЗАДАНИЕ 13
|
С помощью динамической математической среды GeoGebra создайте интерактивную модель «График производной функции». | |
|---|---|
| Программное обеспечение |
математическая среда GeoGebra |
| Дополнительная информация |
Статья «Динамическая математическая программа GeoGebra». |
| Этапы выполнения задания | |
| Комментарий для выполнения задания |
С помощью производной можно увидеть все изменения функции или насколько быстро меняется значение у с изменением значений х. Пусть нарисован график некоторой функции y = f(x). Отметим на графике точку А с абсциссой x0. Проведем в этой точке касательную к графику функции. Мы хотим оценить, насколько увеличилось значение функции при незначительных изменениях аргумента. Для этого рассмотрим тангенс угла наклона прямой к положительному направлению оси Ох. Вспомним, что прямая (касательная) задается уравнением y = kx + b (величина k в этом уравнении называется угловым коэффициентом прямой. k равен тангенсу угла наклона прямой к оси Ох). |
| 1 |
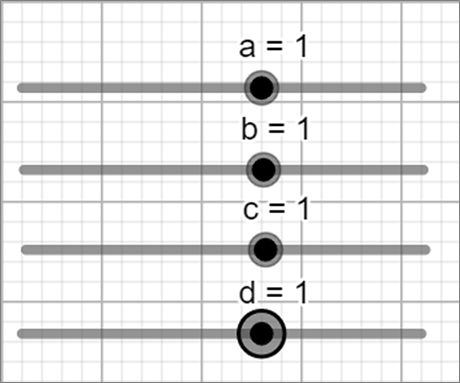
Опишем последовательность наших действий в программе для выполнения чертежа: - Добавление 4 ползунков (a, b, c, d). Примечание. Рекомендуется ознакомиться с информацией в статье «Динамическая математическая программа GeoGebra» и посмотреть видео «Геометрическое значение производной в GeoGebra» (см. помощь) |
| 2 |
Для организации работы с заданием выполните следующие действия: – перейдите по ссылке на сайт GeoGebra. Примечание. Переключение интерфейса программы на русский язык обычно происходит после авторизации. |
| 3 |
На панели инструментов нажмите кнопку Аналогично добавим еще 3 ползунка. Примечание. После выполнения построения определенным инструментом его надо выключать, чтобы не «засорять» чертеж ненужными объектами. |
| 4 |
В области со списком объектов (слева) найдите поле «Ввод» и добавьте в него функцию (наберите текст), коэффициентами которой будут добавленные ползунки (например, у = axd + bx + c). Примечание. Для набора математических выражений используйте буквы латинского (английского) алфавита; После ввода формулы сразу же нарисуется график в специальной области справа. Переместите ползунок d на 2. Примечание. Обратите внимание, программа также прописывает уравнение функции, которая сейчас построена. |
| 5 |
Выберите инструмент Через точку А проводим касательную к графику функции – команда С помощью команды |
| 6 |
В поле «Ввод» (область со списком объектов) добавьте точку В(x(А),k).(координаты не менять!) Для данной точки установите параметр «Оставлять след» (контекстное меню точки – команда «Оставлять след»). 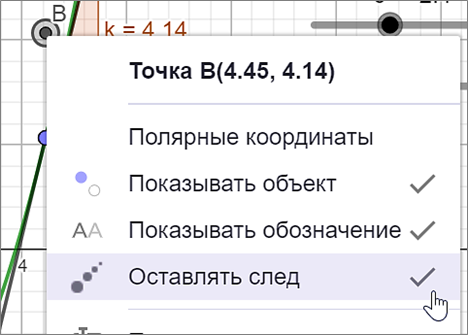 |
| 7 |
Измените формулу функции (переместите ползунки). Примечание. Для удобства построения следа запустите анимацию точки A. |
| 8* |
С помощью команды Примечание. Сначала через точку А необходимо провести прямую, параллельную оси Ох |
| 9 |
Сохраните свой чертеж с названием «График производной функции»: |
| 10 |
Разместите ссылку на интерактивный чертеж на сайте «Математика с компьютером». Для этого: |
| 11 |
Учитель математики может использовать интерактивную модель «График производной функции» при изучении раздела «Производная». |
| 12 |
Измените значения ползунков. Выполните исследование полученных функций. |
| Помощь | |
|
1. Видео «GeoGebra за 19 минут» 2. Видео «Геометрическое значение производной в GeoGebra» (качество 480 р)
|
|