ЗАДАНИЕ 14
|
А) Выполните в динамической математической среде GeoGebra интерактивный геометрический чертеж для иллюстрации теоремы Фалеса: если на одной стороне угла отложить последовательно два отрезка разной длины и через их концы провести параллельные прямые, пересекающие другую сторону угла, то на другой стороне угла отложатся отрезки, пропорциональные данным. | |
|---|---|
| Программное обеспечение |
математическая среда GeoGebra |
| Дополнительная информация |
Статья «Динамическая математическая программа GeoGebra». |
| Этапы выполнения задания | |
| Комментарий для выполнения задания |
В качестве образца будет поэтапно описано выполнение задания А). Примечание. Рекомендуется предварительно ознакомиться с информацией в статье «Динамическая математическая программа GeoGebra». |
| 1 |
Они похожи на действия по построению этого чертежа на листе бумаги. Теперь надо доказать, что Для этого надо найти отношение (частное) этих отрезков (при любом положении точек частное длин отрезков должно быть одинаковым). Посмотреть чертеж |
| 2 |
Для организации работы с заданием выполните следующие действия: – перейдите по ссылке на сайт GeoGebra, скачайте и установите на компьютер программу GeoGebra Classic 6 (geogebra.org/download); Примечание. Переключение интерфейса программы на русский язык обычно происходит после авторизации. |
| 3 |
Настройте внешний вид программы для геометрического чертежа (скройте с области построения координатные оси и сетку).
|
| 4 |
На панели инструментов нажмите кнопку Аналогично постройте луч АС. |
| 5 | Выберите инструмент |
| 6 |
На панели инструментов нажмите кнопку Примечание. После выполнения построения определенным инструментом его надо выключать, чтобы не «засорять» чертеж ненужными геометрическими объектами. |
| 7 |
На панели инструментов нажмите кнопку Примечание. Не забывайте выключать инструмент (кнопка Esc на клавиатуре). |
| 8 |
На пересечении луча АС и прямой, параллельной ВС, поставьте точку E (выберите инструмент |
| 9 |
Далее надо найти длины отрезков для нахождения их частного. Длина отрезка будет отображаться на панели объектов слева. Также информация о длине отрезка появляется на самом чертеже. Аналогично найдите длины отрезков AC и CE. |
| 10 |
Аналогично вычислите отношения длин сторон AE и EС. Убедитесь, что отношения между собой равны. |
| 11 |
Чертеж является динамичным. Если переместить по прямой точку D, то будут изменяться не только длины отрезков, но и отношения этих отрезков. |
| 12 | Сохраните рисунок. Его можно использовать при объяснении, обобщении и систематизации соответствующих тем. |
| 13 | Самостоятельно выполните задание Б) С помощью инструментов динамической математической среды GeoGebra разделите отрезок на пять равных частей. |
| Помощь | |
|
1. Видео «GeoGebra за 19 минут» 2. Видео «Математика 8 (геометрия, задание 14)»
|
|
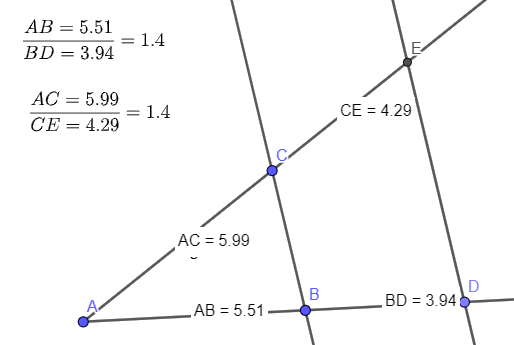

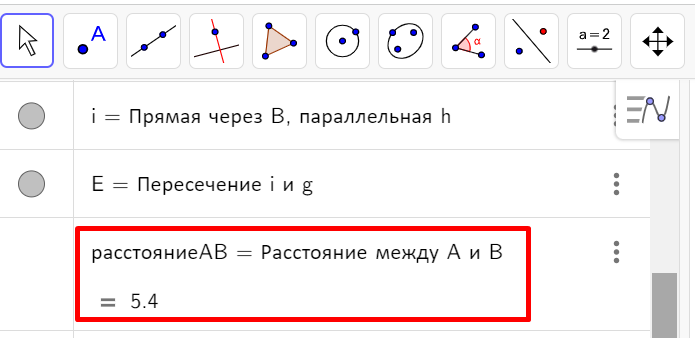
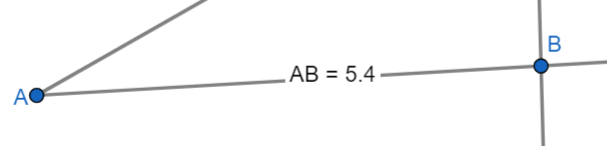
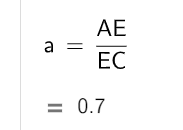 Для вычисления отношения между длинами сторон в свободное текстовое поле на панели объектов слева с помощью клавиатуры введите: АВ/BD и нажмите кнопку Enter.
Для вычисления отношения между длинами сторон в свободное текстовое поле на панели объектов слева с помощью клавиатуры введите: АВ/BD и нажмите кнопку Enter.