Фізіка. 11 клас

Тэорыя Бора прапанавала фізікам карыстацца па панядзелках,
серадах і пятніцах класічнымі законамі,
а па аўторках, чацвяргах і суботах — квантавымі.

Вільям Брэг-старэйшы

Мадэль атама Бора не змагла даць вычарпальныя адказы на пытанні аб устойлівасці атама, аб дыскрэтнасці спектра яго выпраменьвання. Толькі з развіццём квантавай механікі з выкарыстаннем новага матэматычнага апарата ўдалося пабудаваць завершаную мадэль будовы атама, якая дазваляе зразумець законы мікрасвету.

У класічнай механіцы рух часціцы апісваецца заданнем яе каардынат і імпульсу (скорасці) у кожным пункце траекторыі. Каб разлічыць параметры руху любой складанай сістэмы, дастаткова задаць каардынаты і імпульсы (скорасці) ўсіх часціц, якія ўваходзяць у сістэму, у пачатковы момант часу і ўмовы, пры якіх адбываецца рух (дзеючыя сілы, палі). Пасля гэтага, выкарыстаўшы ўраўненні руху (другі закон Ньютана), можна знайсці каардынаты і імпульсы (скорасці) у любы момант часу, г. зн. вызначыць, дзе будзе знаходзіцца часціца ў той ці іншы момант часу.

Пры пераходзе ў абсяг мікрасвету аказваецца, што такі спосаб немагчыма прымяніць. Для апісання з'яў мікрасвету была распрацавана квантавая механіка. Квантавая механіка — раздзел фізікі, у якім вывучаюцца ўласцівасці і паводзіны мікрачасціц, а таксама сувязь велічынь, якія характарызуюць часціцы, з фізічнымі велічынямі, якія непасрэдна вымяраюцца ў эксперыментах.

Вынікі эксперыментаў паказваюць, што мікрааб’екты маюць адначасова карпускулярныя і хвалевыя ўласцівасці. Так, напрыклад, электрон з'яўляецца часціцай, якая мае пэўную масу і зарад, але пры яго руху вакол ядра неабходна ўлічваць яго хвалевыя ўласцівасці, паколькі ў яго адсутнічае пэўная траекторыя руху і дакладнае размяшчэнне ў прасторы. Для тлумачэння падвойных паводзін мікрааб’ектаў патрабаваўся кардынальны перагляд існуючых уяўленняў.

У квантавай механіцы рух часціцы апісваецца хвалевай функцыяй  — функцыяй каардынат і часу. Ведаючы хвалевую функцыю часціцы, выкарыстаўшы вымяральныя прыборы, можна атрымаць звесткі аб паводзінах гэтай часціцы і аб выніках любога яе ўзаемадзеяння. Пры гэтым хвалевая функцыя характарызуе імавернасць любога выніку вымярэння. Квадрат яе модуля  вызначае імавернасць знаходжання часціцы ў наваколлі пункта з каардынатамі (x,y,z) у момант часу t. У квантавай механіцы, нават калі задаць усе пачатковыя ўмовы ў нейкі момант часу і цалкам рашыць сістэму ўраўненняў для хвалевых функцый, можна ўстанавіць толькі імавернасць тых ці іншых працэсаў. Напрыклад, імавернасць выявіць электрон ў дадзеным месцы можа апынуцца ў 10 разоў большай за імавернасць яго знаходжання ў іншым месцы. Аднак прадказаць яго становішча са стопрацэнтнай дакладнасцю, як гэта было ў класічнай механіцы, ужо нельга.

Электроны ў атаме набліжана разглядаюцца як «размазаныя» ў прасторы і ўтвараючыя вакол ядра электроннае воблака (гл. мал. 198-1). Электроннае воблака, якое адпавядае асноўнаму стану, канцэнтруецца ў абсягу, які знаходзіцца дастаткова блізка да ядра. Для ўзбуджаных станаў яно размяркоўваецца на ўсё большыя адлегласці ад ядра. Слабей за ўсё звязаны з ядром электроны самай знешняй абалонкі, якія вызначаюць памеры атама ў цэлым.

У залежнасці ад таго, што і як вымяраецца ў пэўным стане часціцы, на першы план выступаюць то яе карпускулярныя ўласцівасці, то яе хвалевыя ўласцівасці. Прымяненне хвалевай функцыі дазваляе апісаць як карпускулярныя, так і хвалевыя ўласцівасці мікрачасціц.

Найважнейшым фізічным палажэннем квантавай механікі з'яўляецца знакаміты прынцып няпэўнасці Гейзенберга, згодна з якім:

ні пры якім павелічэнні дакладнасці вымярэнняў немагчыма дабіцца таго, каб здабытак няпэўнасцей вымярэння каардынаты і імпульсу часціцы стаў меншым за пастаянную Планка.

Такім чынам, у квантавай механіцы для сістэмы, якая знаходзіцца ў некаторым вядомым стане, можна прадказаць вынікі вымярэнняў або яе становішча, або яе імпульсу паасобку. Імавернасная інтэрпрэтацыя прадказвае, што вымярэнні аднолькавым дэтэктарам для аднолькавых часціц у аднолькавых станах адной і той жа велічыні будуць даваць розныя вынікі. У прыватнасці, імавернасць каардынаты вызначаецца як .

Адна з найважнейшых высноў квантавай механікі заключаецца ў тым, што існуе самы нізкі ўзровень энергіі, якому адпавядае асноўны стан сістэмы. У гэтым стане сістэма валодае мінімальнай кінетычнай энергіяй, прычым  ≠ 0.. 

Табліца 9-1. Квантавыя лікі
Квантавы лік	Сімвал	Значэнні	Поўны лік значэнняў
Галоўны	n	1,2,3 ...
Арбітальны	l	0,1, ... , n - 1	n (пры зададзеным n)
Магнітны	ml	- l, - l + 1, ... l - 1	2l +1 (пры зададзеным l)
Спінавы	ms		2

У квантавай механіцы для задання кожнага стану электрона ў атаме неабходны чатыры розныя квантавыя лікі n, l, m_l, m_s. У табліцы 9-1 дадзены дапушчальныя значэнні ўсіх чатырох квантавых лікаў электрона.

Разгледзім асновы квантава-механічнага апісання найбольш простага атама — атама вадароду. Квантавы лік з мадэлі атама Бора захоўваецца пад назвай галоўнага квантавага ліку. Ён прымае цэлалікавыя значэнні ад 1 да . Ад яго залежаць поўная энергія стану атама вадароду:

, .

Лік l называецца арбітальным квантавым лікам і (пры зададзеным ) прымае цэлалікавыя значэнні: 

.

Лік m_l называецца магнітным квантавым лікам і (пры зададзеным l ) прымае цэлалікавыя значэнні ад -l да +l :

.

Для апісання станаў электрона ў атаме ўводзіцца яшчэ адзін квантавы лік — спінавы , які прымае два значэнні:

.

Гэта звязана з тым, што пры зададзеных n, l, m_l электрон можа знаходзіцца ў двух розных станах, якія характарызуюцца праекцыяй спіна.

Аўстрыйскі фізік-тэарэтык Вольфганг Паўлі прапанаваў простае правіла (прынцып забароны Паўлі) — у адным і тым жа квантавым стане можа знаходзіцца не больш за азін электрон.

Паводле гэтага прынцыпу два электроны не могуць мець аднолькавыя наборы квантавых лікаў, і на яго аснове тлумачыцца наяўнасць груп з 2, 8, 18 і 32 элементаў перыядычнай табліцы Мендзялеева.

Гэтыя групы элементаў з'яўляюцца вынікам прынцыпу забароны Паўлі, а таксама квантава-механічнага правіла, згодна з якім значэнне квантавага ліку l не перавышае n-1(0 ≤ l ≤ n-1), а квантавы лік m пабягае шэраг цэлалікавых значэнняў ад -l 
да  +l +l (- l ≤ m ≤ + l).

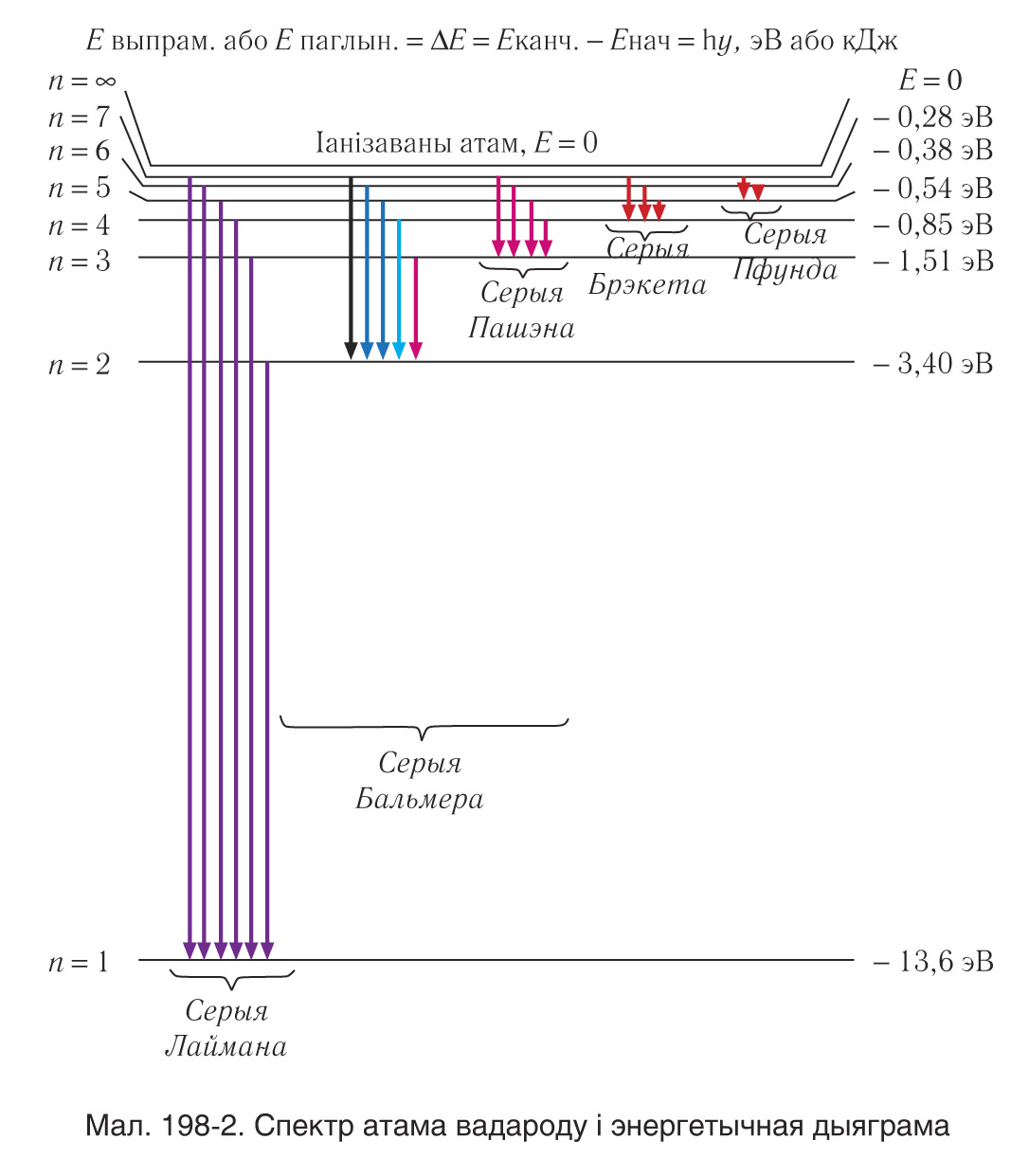
Атам вадароду можа мець адно і тое ж значэнне энергіі, знаходзячыся ў розных станах (мал. 198-2). Энергія атама вадароду залежыць толькі ад галоўнага квантавага ліку n , але ўзроўню энергіі з зададзеным n адпавядаюць некалькі станаў, якія адрозніваюцца значэннямі l, m_l, m_s. Станы з зададзенымі значэннямі n, l прынята абазначаць як 1_s, 2_s, 2_p, 3_s, .., дзе лічбы абазначаюць значэнні n, а літары  s,p,d,f, ...— адпаведныя значэнні l = 0,1,2,3, ... . Узровень, якому адпавядае толькі адзін квантавы стан, называецца нявыраджаным.

Поўны лік усіх магчымых станаў электрона з рознымі l і m пры фіксаваным значэнні галоўнага квантавага ліку n, атрымліваецца роўным n². З улікам двух магчымых значэнняў спіна агульны лік электронаў у абалонцы аказваецца роўным 2n². Гэта і ёсць максімальны лік электронаў у абалонцы з нумарам n.

Спектр выпраменьвання (паглынання) атама вадароду можна цалкам апісаць як вынік пераходаў атама з адных станаў, апісваемых квантавымі лікамі n, l, m_l, m_s, у іншыя, апісваемыя іншым наборам. Аднак, як даказана тэарэтычна і пацверджана эксперыментальна, дазволены не ўсе пераходы, а толькі тыя, што задавальняюць правілы адбору.

Правілы адбору датычацца змяненняў арбітальнага l і магнітнага m_s квантавых лікаў пры пераходах з выпраменьваннем (г. зн. выпусканнем або паглынаннем). Іх змяненне задавальняе ўмовы:

, .

У той жа час правіла адбору не накладвае ніякіх абмежаванняў на змяненні галоўнага квантавага ліку n.

Сукупнасць электронаў у шматэлектронным атаме, якія маюць адзін і той жа галоўны квантавы лік, называюць электроннай абалонкай або слоем.

Асноўныя законы квантавай механікі былі адкрыты ў 1900—1928 гг. У гэты ж час адбылося яе станаўленне як новай навукі — паўнапраўнага раздзела тэарэтычнай фізікі. У гэты час былі прапанаваны новыя фундаментальныя ідэі — кванта энергіі і святла, стацыянарных станаў атамных сістэм і пераходаў паміж імі, прынцыпу адпаведнасці і карпускулярна-хвалевага дуалізму для выпраменьвання і мікрачасціц.

Рашыўшы задачу апісання найпрасцейшага з атамаў — атама вадароду, квантавая механіка ў цяперашні час прымяняецца для рашэння разнастайных праблем фізікі мікраскапічных з'яў — у тэорыі атамаў і малекул, ядзер, элементарных часціц, у тэорыі сутыкненняў і тэорыі выпраменьвання. Як было вызначана, квантавыя ўласцівасці часціц праяўляюцца ў такіх фізічных з'явах, як звышправоднасць, ферамагнетызм, звышцякучасць.

У 1932 г. Вернеру Гейзенбергу была прысуджана Нобелеўская прэмія па фізіцы за распрацоўку асноў квантавай механікі. У 1933 г. «за адкрыццё новых форм атамнай тэорыі» Эрвін Шродзінгер быў удастоены Нобелеўскай прэміі па фізіцы. У 1945 г. В. Паўлі была прысуджана Нобелеўская прэмія па фізіцы за адкрыццё прынцыпу забароны. У 1954 г. М. Борн быў узнагароджаны Нобелеўскай прэміяй за фундаментальныя даследаванні ў квантавай механіцы, асабліва за статыстычную інтэрпрэтацыю хвалевай функцыі.