Фізіка. 11 клас

Змяненне ўяўленняў аб уласцівасцях прасторы і часу выклікала з’яўленне новых поглядаў на сувязь энергіі цела з яго масай. У чым сутнасць знакамітай формулы Эйнштэйна Е0 = mc2? Дзе яна знаходзіць сваё прымяненне?

Сфармуляваныя Эйнштэйнам пастулаты, пакладзеныя ў аснову спецыяльнай тэорыі адноснасці (СТА), прывялі да перагляду ім поглядаў на класічную (ньютанаўскую) механіку. Класічныя выразы для імпульсу і энергіі былі зменены для новай, удакладненай формы запісу законаў захавання імпульсу і энергіі. Такім чынам, тэорыя адноснасці запатрабавала перагляду і ўдакладнення законаў механікі, від якіх заставаўся нязменным з часоў Ньютана.

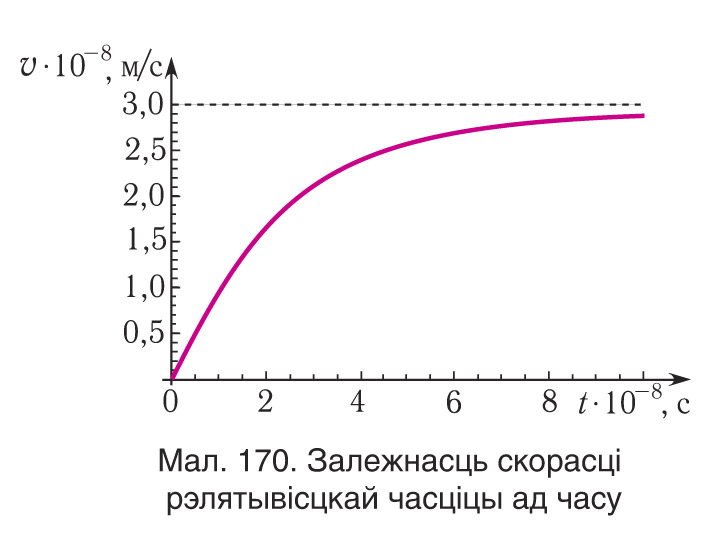
Неабходнасць змянення дынамікі відавочная хаця б таму, што паводле законаў Ньютана любое цела можна ў прынцыпе разагнаць да любой скорасці. Прыкладзём да цела масай m, якое знаходзіцца ў стане спакою, пастаянную сілу . Выкарыстаўшы другі закон Ньютана, знойдзем, што да моманту часу t цела набудзе скорасць . Такім чынам, у рамках класічнай механікі пры  скорасць цела v перавысіла б скорасць святла c, што супярэчыць вынікам эксперыментаў і асноўным палажэнням СТА. Залежнасць скорасці v цела ад часу t у рэлятывісцкім выпадку паказана на малюнку 170.

Якія ж суадносіны дынамікі неабходна было змяніць пры пераходзе ад механікі Ньютана да СТА, а якія засталіся нязменнымі?
Захавалі свой выгляд законы змянення імпульсу і энергіі цела:

,

(1)

дзе  A — работа, якую выконвае сіла .

Змяніліся суадносіны, якія выражаюць залежнасць імпульсу і энергіі цела ад яго скорасці:

, .

Ураўненні дынамікі трэба змяніць так, каб яны заставаліся нязменнымі пры пераходзе ад адной інерцыяльнай сістэмы адліку да іншай паводле прынцыпу адноснасці. У выпадку малых скарасцей (v << c) ураўненні рэлятывісцкай дынамікі павінны пераходзіць у класічныя, бо ў гэтай галіне іх справядлівасць пацвярджаецца шматлікімі эксперыментамі.

У СТА эфектыўна вукарыстоўваецца фундаментальная дынамічная суадносіна, якая звязвае поўную энергію E і  імпульс  свабоднай часціцы масай , якая рухаецца са скорасцю :

(1-1)

прычым маса m тут — тая ж самая велічыня, што і ў класічнай механіцы.

Выраз для імпульсу  у класічнай механіцы не задавальняе прынцыпы СТА, законы захавання энергіі і імпульсу, а таксама суадносіну (1-1). Таму ў СТА рэлятывісцкі імпульс вызначаецца новым выразам:

.

(1-2)

Асабліва важна адзначыць, што формулы (1-1) і (1-2) апісваюць рух часціц ва ўсім інтэрвале магчымых скарасцей:. Пры руху са скорасцю распаўсюджвання святла (v = c) модуль імпульсу і энергія звязаны суадносінай:

.

(1-3)

Падставіўшы выраз (1-3) у формулу (1-1), атрымаем:

.

Адкуль вынікае, што маса часціцы, якая рухаецца са скорасцю святла ў вакууме, роўна нулю.

Для часціц з ненулявой масай выразім энергію і імпульс праз масу і скорасць. Падставім выраз (1-2) у (1-1):

.

Адсюль атрымаем:

,

(1-4)

дзе лорэнцаўскі множнік.

Падставіўшы выраз (1-4) у (1-2), атрымаем:

.

(1-5)

Такім чынам, для цел, якія рухаюцца са скарасцямі, блізкімі да скорасці распаўсюджвання святла ў вакууме, іх энергія і імпульс вызначаюцца суадносінамі (1-4) і (1-5).

Асноўнае ўраўненне рэлятывісцкай дынамікі па-ранейшаму запісваецца ў выглядзе:

,

(1-6)

дзе:

.

Найважнейшым адрозненнем СТА ад класічнай механікі з’яўляецца тое, што энергія цела не ператвараецца ў нуль, нават калі яно знаходзіцца ў спакоі (v = 0) У гэтым выпадку энергія спакою E₀ цела прапарцыянальна яго масе:

(2)

Такім чынам, у целе, якое знаходзіцца ў стане спакою, хаваецца велізарны запас энергіі. Цяжка пераацаніць практычнае значэнне гэтай нескладанай формулы, паколькі менавіта яна паказала на ўзаемасувязь энергіі і масы рэчыва. Чалавецтва даведалася аб магчымасці атрымання энергіі з рэчыва. На гэтай формуле заснавана ўся энергетыка, у якой энергія спакою паліва пераходзіць у іншыя віды энергіі.
З роўнасці (2) вынікае, што змяненне энергіі спакою цела на  звязана са змяненнем яго масы на  дзе:

.

(3)

Сцверджанне аб тым, што энергія спакою прапарцыянальна масе, а змяненне энергіі спакою звязана са змяненнем масы, называюць законам узаемасувязі масы і энергіі.
Цяжка пераацаніць практычнае значэнне гэтага закону для сучаснай энергетыкі. З яго вынікае, што цела масай m = 1,0 г валодае энергіяй спакою:

.

Гэта энергія эквівалентна энергіі, якая вылучаецца пры згаранні 2000 тон нафты. Так, дзякуючы прагрэсу фізікі ў 1905 г. чалавецтва даведалася аб практычна «невычэрпных» запасах энергіі, якая ўтрымліваецца ў любым рэчыве.

Формула (3) прымяняльная да ўсіх з’яў, у якіх змяняецца ўнутраная энергія рэчыва. Пры працэсах, што адбываюцца на атамна-малекулярным узроўні, змяненні масы зусім малыя. Так, пры поўным ператварэнні лёду ў ваду адноснае змяненне масы  пры награванні на  жалезнага бруска  Пры хімічных рэакцыях адноснае змяненне масы крыху вышэйшае. Напрыклад, пры згаранні метану ў кіслародзе  Для ядзерных рэакцый сітуацыя зусім іншая. Для іх характэрны велічыні  у дзясяткі мільёнаў разоў большыя, чым для хімічных рэакцый.

Згодна з СТА маса часціцы з’яўляецца мерай энергіі, што змяшчаецца ў часціцы ў стане спакою, мерай энергіі спакою. Гэта ўласцівасць масы была невядома ў класічнай механіцы.

Маса элементарнай часціцы з’яўляецца адной з яе найважнейшых характарыстык, якую імкнуцца вымераць найбольш дакладна. Яе вызначаюць з формулы (1-1)

.

(3-1)

пасродкам вымярэння энергіі і модуля імпульсу часціцы.

У СТА, гэтаксама як і ў класічнай механіцы, маса ізаляванай сістэмы цел захоўваецца, г. зн. не змяняецца з цягам часу.

Кінетычную энергію E_к вызначаюць як рознасць поўнай энергіі E і энергіі спакою E₀:

.

(3-2)

У выпадку, калі скорасць часціцы імкнецца да скорасці распаўсюджвання святла, кінетычная энергія часціцы імкнецца да бясконцасці. Гэта азначае, што часціцу, якая мае некаторую масу, немагчыма разагнаць да скорасці распаўсюджвання святла.

Атрыманыя формулы прымяняльныя да любога складанага цела, што складаецца з многіх часціц, прычым пад масай m трэба разумець поўную масу цела, а пад скорасцю  — яго скорасць руху як цэлага. Энергія цела ў стане спакою змяшчае ў сабе, акрамя энергій спакою часціц, што ў яго ўваходзяць, таксама кінетычную энергію часціц і энергію іх узаемадзеяння.

Пры малых скарасцях (v << c), г. зн.  і для релятывісцкага множніка γ можна карыстацца прыбліжанай суадносінай  пры x<< 1. (Можаце праверыць гэту суадносіну лікава на калькулятары, напрыклад пры)

Тады:

.

(3-3)

Выраз для рэлятывісцкага імпульсу (1-5) і рэлятывісцкай кінетычнай энергіі (3-2) пераходзяць у класічныя, якія выкарыстоўваюцца ў класічнай механіцы:

, .

Як бачым, тэорыя Эйнштэйна не супярэчыць тэорыі Ньютана. Больш за тое, яна «змяшчае» яе ў сабе як прыватны выпадак пры малых скарасцях.

Згодна з прынцыпам адпаведнасці любая новая фізічная тэорыя, якая прэтэндуе на больш глыбокае апісанне фізічных з'яў (адпаведна і на больш шырокую галіну прымянення), павінна ўключаць у сябе класічную (ньютанаўскую) тэорыю як гранічны выпадак.

Гэты прынцып выказвае патрабаванне пераемнасці ведаў. У адпаведнасці з ім, новая тэорыя павінна ўключаць у сябе папярэднюю тэорыю і абазначаць межы прымяняльнасці яе ідэй і метадаў разліку. Пры скарасцях руху  законы рэлятывісцкай механікі пераходзяць у законы класічнай механікі. На практыцы ўсе формулы СТА пераходзяць у формулы класічнай механікі, у здагадцы, што  .