Физика. 11 класс

Законы отражения и преломления света широко используются для управления ходом световых пучков. Для отражения света в приборах применяются зеркала и призмы, для преломления — призмы, плоскопараллельные пластинки, линзы. Зеркала, призмы, пластинки и линзы являются элементами, комбинируя которые создают различные оптические приборы.

Рассмотрим отдельные элементы оптических приборов.

Плоскопараллельная пластинка

Рассмотрим ход светового луча от источника в плоскопараллельной пластинке  толщиной, находящейся в воздухе (рис. 138, а). Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом  на первую границу, имеем (рис. 138, б)

sinα = nsinγ, nsinα1 = sinγ1

Здесь γ — угол преломления на первой границе,  α₁— угол падения на вторую границу, γ₁ — угол преломления на второй границе,  —  абсолютный показатель преломления вещества пластинки.

Накрест лежащие углы γ и α₁ при параллельных прямых  AD и BK (перпендикулярах к первой и второй параллельным границам) равны, т.е. α₁ = γ. Следовательно, sinα = nsinγ = nsinα₁  = sinγ₁. Откуда следует, что:

α = γ1.

(1)

Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается на некоторое расстояние h=BC перпендикулярно своему начальному направлению (см. рис. 138, б)

Соответственно, все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом не равным нулю, будут также казаться смещенными.

Как видно из рисунка 138, а лучи, отраженные от верхней и нижней граней пластинки параллельны друг другу на выходе из неe.

Найдем, от каких параметров пластинки зависит смещение h луча.

Из   следует, что:

h= BC = ABsin(α - γ).

Из  имеем:

Откуда:

С учетом закона преломления  и тригонометрического тождества sin²γ + cos²γ  = 1 находим:

.

Окончательно, расстояние h между направлениями входящего и выходящего лучей можно определить из соотношения:

.

(1-1)

Как видно из соотношения (1-1), смещение h луча при данном угле падения α зависит от толщины d пластинки и ее показателя преломления n.

Трехгранная призма

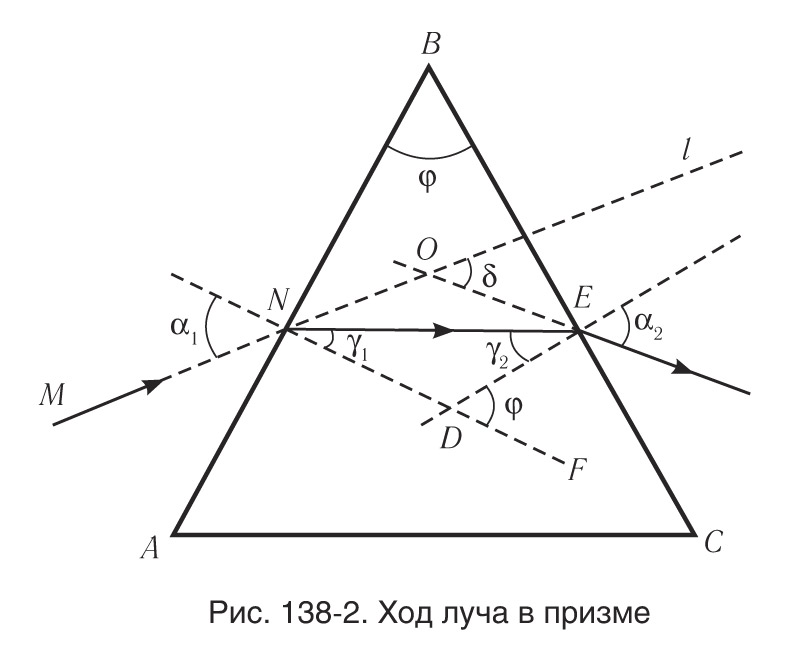
Рассмотрим ход луча в трехгранной призме. Пусть световой луч NM падает под углом α₁ на боковую грань трехгранной призмы ABC, сечение которой показано на рисунке 138-2. Призма, изготовленная из вещества с абсолютным показателем преломления n₂, находится в среде с абсолютным показателем преломления n₁. Грани призмы, проходя через которые лучи света преломляются, называются преломляющими. Грань, лежащая напротив преломляющего угла, называется основанием призмы. Угол φ при вершине B   называется преломляющим углом призмы.

Пусть луч  и  лежат в одной плоскости — плоскости листа книги. Из закона преломления света находим угол преломления γ₁:

.

(1-2)

Если показатель призмы n₂ > n₁, то преломленный луч  падает на вторую боковую грань призмы под углом γ₂. Полного отражения на второй преломляющей грани не происходит при условии , и луч выходит из призмы под углом α₂. Его находим из закона преломления: 

.

(1-3)

Отклонение от начального направления луча  вследствие преломлений на гранях призмы определяется LOE = δ (см. рис. 138-2). Угол  между направлениями входящего и выходящего лучей называется углом отклонения. Рассмотрим . В нем . По теореме о внешнем угле треугольника находим:

γ1 + γ2 = φ.

(1-4)

Применим эту же теорему к :

(α1 - γ1) + (α2 - γ2) = δ.

(1-5)

Из формул (1-4) и (1-5) определим связь угла падения α₁, угла преломления α₂ с преломляющим углом призмы φ и углом отклонения δ выходящего луча от начального направления:

δ = α1 + α2 - φ.

(1-6)

В результате получили систему уравнений (1-2), (1-3), (1-4), (1-6):

(1-7)

Система уравнений (1-7) позволяет решить задачу на прохождение луча света через трехгранную призму без полного отражения на ее гранях.

Если угол падения α₁ на грань призмы и преломляющий угол призмы φ малы, то малыми будут и углы γ₁, γ₂, α₂  . Поэтому в законах преломления (1-2) и (1-3) отношение синусов можно заменить отношением углов, выраженных в радианах, т.е. 

.

(1-8)

Подставляя выражения для (1-8) α₁ и α₂ в соотношение (7), находим:

.

(1-9)

Из соотношения (1-9) следует, что: во-первых, чем больше преломляющий угол φ, тем больше угол отклонения δ лучей призмой; во-вторых, угол отклонения δ лучей увеличивается с ростом абсолютного показателя преломления n₂ вещества призмы. Как видно из рисунка 138-2, луч света, проходя через трехгранную призму, отклоняется к ее утолщенной части, если абсолютный показатель преломления вещества призмы больше абсолютного показателя преломления окружающей среды (n₁ > n₂).

Трехгранная призма (рис. 139). Как видно из рисунка 139 луч света, проходя через трехгранную призму, отклоняется от своего начального направления распространения к основанию (утолщенной части) призмы. Подчеркнем, что это справедливо в том случае, если абсолютный показатель преломления вещества призмы больше абсолютного показателя преломления окружающей среды . Обратите внимание (см. рис. 139), что если на призму падает луч белого света, то после прохождения призмы на экране наблюдается разноцветная полоска, содержащая набор цветов — от красного до фиолетового. Исаак Ньютон, впервые проделавший данный эксперимент, назвал эту полоску спектром. Порядок следования цветов в спектре легко запомнить с помощью известной фразы:           красный — 770—630 нм                    каждый           оранжевый — 630—590 нм                охотник           желтый — 590—570 нм                      желает           зеленый — 570—495 нм                     знать,           голубой, синий — 495—435 нм         где сидят           фиолетовый — 435—390 нм              фазаны