§ 26. Алгебра логікі

26.1. Лагічныя выказванні

Працэсар камп’ютара выконвае арыфметычныя і лагічныя аперацыі над двайковымі кодамі.

Для таго каб мець уяўленне пра будову камп’ютара, неабходна пазнаёміцца не толькі з арыфметычнымі, але і з асноўнымі лагічнымі элементамі, якія ляжаць у аснове яго пабудовы.

Для разумення прынцыпу работы такіх элементаў разгледзім асноўныя паняцці алгебры логікі.

Алгебра логікі (англ. algebra of logic) — адзін з асноўных раздзелаў матэматычнай логікі, у якім метады алгебры выкарыстоўваюцца ў лагічных пераўтварэннях.

Аналогію паміж алгебрай і логікай паклаў у аснову свайго лагічнага вучэння заснавальнік алгебры логікі англійскі матэматык і логік Д. Буль (1815—1864).

Любое выказванне Буль запісваў з дапамогай сімвалаў распрацаванай ім мовы і атрымліваў «ураўненні», праўдзівасць ці непраўдзівасць якіх можна было даказаць, зыходзячы з пэўных лагічных законаў.

Лагічнае выказванне — любы апавядальны сказ, у адносінах да якога можна адназначна сцвярджаць, што яго змест праўдзівы — 1 ці непраўдзівы — 0.

Сучасная алгебра логікі з’яўляецца раздзелам матэматычнай логікі і вывучае лагічныя аперацыі над выказваннямі з пункту гледжання іх праўдзівага значэння.

Праўдзівасць ці непраўдзівасць выказванняў залежыць ад праўдзівасці і непраўдзівасці зыходных (простых) выказванняў і сэнсу лагічных аперацый над выказваннямі (прыклад 26.1). Такім чынам, вызначэнне праўдзівасці некаторага лагічнага выразу — гэта вызначэнне значэння некаторай лагічнай функцыі.

Лагічная функцыя — функцыя, якая прымае значэнні 0 ці 1 у выніку лагічных аперацый над лагічнымі пераменнымі.

Спосабы задання лагічнай функцыі:

1) слоўнае апісанне;

2) табліца праўдзівасці;

3) формула, запісаная з дапамогай літар, знакаў лагічных аперацый і дужак;

4)  кімбінацыйная схема, складзеная з лагічных элементаў;

5)  каардынатны спосаб (карта Карно);

6)  дыяграма Вена (Эйлера).

(Разгледзьце прыклад 26.2.)

Вобласці ўжывання алгебры логікі:

1) у якасці сродку алгарытмічнага апісання ў мовах праграміравання для вызначэння лагічных умоў;

2) для фарміравання лагічных выказванняў у матэматычнай логіцы, лінгвістыцы, тэорыі штучнага інтэлекту;

3) у распрацоўцы і апісанні дыскрэтных тэхнічных сістэм;
пры аналізе і сінтэзе лагічных устройстваў.

Пример 26.1. Логические высказывания.

  1. «Мінск — сталіца Грэцыі» — зыходнае выказванне, значэнне якога непраўдзівае ( A = 0). «НЯпраўда, што Мінск — сталіца Грэцыі» — выказванне, значэнне якога праўдзівае (begin mathsize 14px style top enclose A end style = 1).
  2. «Мінск — сталіца Беларусі», «Масква — сталіца Расіі» — зыходныя выказванні, значэнне якіх праўдзівае (A = 1, B = 1). «Мінск — сталіца Беларусі І Масква — сталіца Расіі» — выказванне, значэнне якога праўдзівае (A & B = 1 ).
  3. «Мінск — сталіца Беларусі», «Масква — сталіца Балгарыі» — зыходныя выказванні. Значэнне першага выказвання праўдзівае, а другога непраўдзівае (A = 1, B = 0). Мінск — сталіца Беларусі АБО Масква — сталіца Балгарыі» — выказванне, значэнне якога праўдзівае (A V B = 1).

Карта Карно — табліца, пабудаваная так, што ў яе суседнія клеткі трапляюць сумежныя наборы пераменных функцый — наборы, якія адрозніваюцца значэннем адной пераменнай (у адзін набор гэта пераменная ўваходзіць у прамой форме, а ў іншы — у адваротнай).

Карты Карно былі прапанаваны ў 1952 г. Эдвардам В. Вейчам (амерыканскім вучоным у галіне кібернетыкі) і ўдасканалены ў 1953 г. Морысам Карно, каб спрасціць праектаванне лічбавых сістэм.

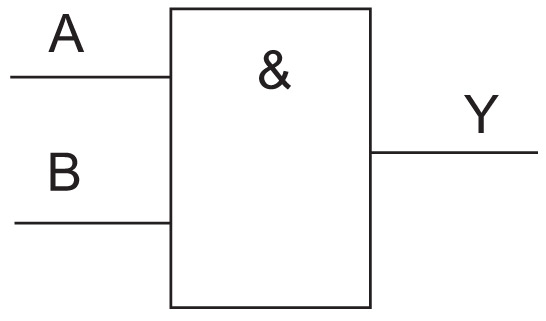
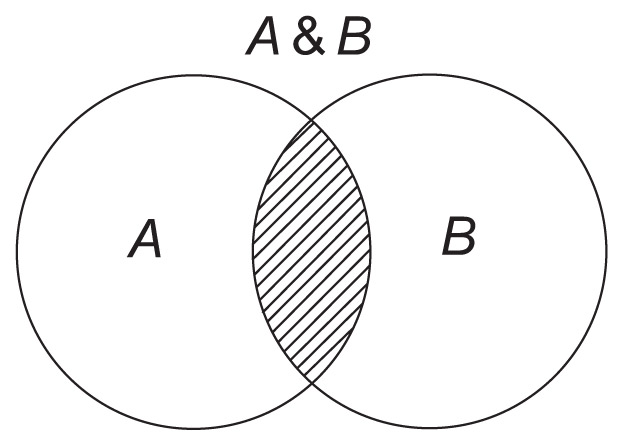
Морыс Карно — амерыканскі фізік

Прымер 26.2. Спосабы задання лагічнай функцыі.

1. Функцыя дзвюх пераменных прымае значэнне 1, калі гэтыя пераменныя роўныя 1, а ва ўсіх іншых выпадках функцыя роўная 0.

 2.

A

B

A & B

0

0

0

0

1

0

1

0

0

1

1

1

3. Y = A & B

4. 

5. 

 

A

begin mathsize 14px style top enclose A end style

B

1

0

begin mathsize 14px style top enclose straight B end style

0

0

6. 

Аналіз лагічных устройстваў — гэта пошук аналітычнага выразу, які апісвае работу сістэмы.

Сінтэз лагічных устройстваў — адваротная задача: стварэнне тэхнічнага ўстройства на аснове матэматычнага апісання сродкамі алгебры логікі.

У камп’ютарных устройствах ужываюцца электрычныя схемы, якія складаюцца з мноства пераключальнікаў. Пераключальнік можа знаходзіцца толькі ў двух станах: замкнутым і разамкнутым. У першым выпадку ток праходзіць, у другім — не. Апісваць работу такіх схем вельмі зручна з дапамогай алгебры логікі. У залежнасці ад становішча пераключальнікаў можна атрымаць ці не атрымаць сігналы на выхадах.