§ 18. Сортировка одномерного массива

18.5. Быстрая сортировка

Рассмотрим еще один алгоритм сортировки, который является существенным улучшением алгоритма сортировки обменом. Сортировка обменом является одним из самых неэффективных алгоритмов сортировки. Однако усовершенствованный алгоритм позволяет получить результат намного быстрее, поэтому, его изобретатель Чарльз Хоар назвал этот алгоритм быстрой сортировкой (quicksort). Высокая производительность достигается за счет того, что происходит обмен элементов на больших расстояниях.

В массиве выбирается некоторый элемент, называемый опорным. Для остальных элементов производятся перестановки таким образом, чтобы слева от опорного находились элементы не больше его, а справа — не меньше. Тем самым массив разбивается на две части:

  • не отсортированные элементы слева от опорного элемента;
  • не отсортированные элементы справа от опорного элемента.

В дальнейшем для каждой части действия повторяются. Следует заметить, что конечная позиция опорного элемента необязательно совпадает с его позицией до перестановок элементов.

Рассмотрим ее работу на том же массиве а = {9, 6, 0, 2, 7, 3, 1, 5} (пример 18.14).

Формальное описание алгоритма:

1. Заведем два указателя: левый и правый, которые позволят перемещаться по элементам массива с начала и с конца.

2. В качестве опорного элемента выберем элемент, стоящий на среднем месте.

3. Слева от опорного элемента найдем не меньший, а справа — не больший, чем опорный, и поменяем их местами.

4. Обмен элементов производим, пока указатель из левой части не станет больше указателя из правой части.

5. Рекурсивно обрабатываем 2 части массива: от начала до значения правого указателя и от значения левого указателя до конца.

Рекурсивная функция быстрой сортировки приведена в примере 18.15.

В худшем случае алгоритм требует порядка n2 операций сравнения и столько же перестановок элементов в массиве. Однако такие случаи встречаются нечасто (пример 18.16). В среднем, если при каждом рекурсивном вызове массив делится на две почти равные части, то количество требуемых операций будет порядка nk, где значение k определяется из равенства 2k = n. Значение k также определяет размер дополнительной памяти для хранения стека рекурсивных вызовов.

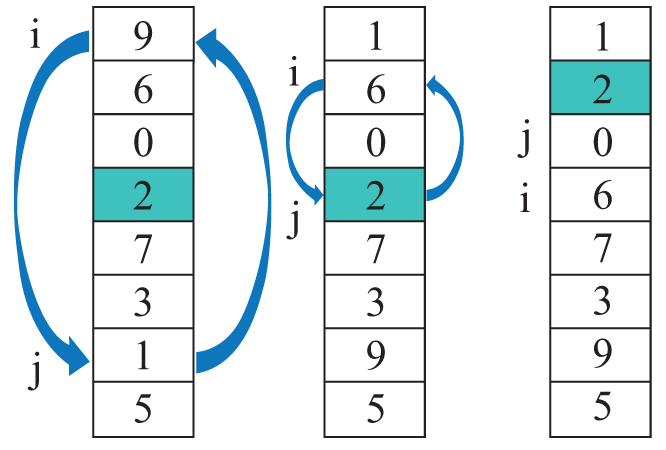
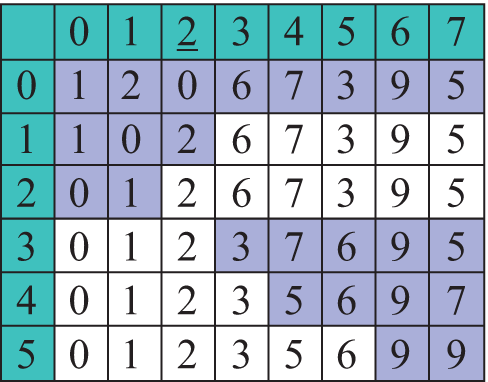
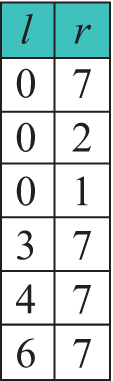
Пример 18.14. Быстрая сортировка. Первый проход по массиву.

Переменные i и j — индексы элементов, подлежащих обмену. Сначала i = l = 0, j = r = 7 (переменные l и r — левая и правая границы обрабатываемой части массива). В конце i = 3, j = 2 (i > j), поэтому обмены больше не производятся. Дальше функция по отдельности работает на подмассивах c границами [0, 2] и [3,7].

Дальнейшие этапы работы алгоритма:

   

Пример 18.15. Функция быстрой сортировки.

void quicksort(vector <int> &d, int l, int r) {

  int pivot = d[(l + r) / 2];

  int i = l, j = r;

  while (i <= j) {

    while (d[i] < pivot)

      i++;

    while (d[j] > pivot)

      j--;

    if (i <= j) {

      swap (d[i], d[j]);

      i++;

      j--;

    }

  }

  if (l < j)

    quicksort(d, l, j);

  if (i < r)

    quicksort(d, i, r);

}

В ранних реализациях быстрой сортировки, как правило, опорным выбирался первый элемент. Такой выбор снижал производительность на отсортированных массивах. Для улучшения эффективности может выбираться средний, случайный элемент или (для больших массивов) медиана[1] первого, среднего и последнего элементов.

Пример 18.16. Примеры ситуаций, когда быстрая сортировка не эффективна:

  • если она применяется для сортировки уже отсортированных массивов;
  • если после обменов получается, что один из подмассивов для нового рекурсивного вызова состоит из одного элемента, а другой из n – 1 элемента;
  • если количество элементов мало (n < 32).

Рекурсивные вызовы являются затратными операциями, и для небольших массивов их количество будет близким к количеству элементов. Поэтому в случае небольших объемов данных  используют нерекурсивные методы сортировки, например сортировку вставками или выбором.

*В математике для определения числа k(2k = n) пользуются функцией log[2]. Алгоритм быстрой сортировки в среднем использует порядка nlogn   сравнений и обменов[3], а также порядка  дополнительной памяти.

[1] Медианой трех различных значений будет то, которое не равно ни минимальному, ни максимальному. Например, для значений 3, 100 и 25 медианой будет 25.

[2] Если 2k = n, то log2n = k.

[3] Кормен, Т. Алгоритмы: построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн., 3-е издание. — М.: «Вильямс», 2013.