§ 18. Сортировка одномерного массива
| Сайт: | Профильное обучение |
| Курс: | Информатика. 10 класс (Повышенный уровень) |
| Книга: | § 18. Сортировка одномерного массива |
| Напечатано:: | Гость |
| Дата: | Среда, 20 Август 2025, 21:19 |
18.1. Понятие сортировки массива
|
Сортировкой называется процесс упорядочения последовательности элементов по какому-либо признаку. С сортировкой вы уже сталкивались при работе с электронными таблицами. Там можно было упорядочить числовые значения в порядке возрастания или убывания, а строковые — в алфавитном (или обратном алфавитному) порядке (пример 18.1). В отсортированном виде хранятся данные в списке контактов в смартфоне (в алфавитном порядке) или письма в электронном почтовом ящике (в порядке получения), данные в различных справочниках и энциклопедиях. Задача сортировки состоит в такой перестановке элементов последовательности, чтобы для двух соседних элементов выполнялось условие того, что они находятся в порядке. Порядок элементов определяет функция сравнения, которая на любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно. Таким образом, сортировка множества элементов возможна тогда, когда для этого множества введено понятие порядка. Порядок, при котором на первом месте в отсортированной последовательности будет находиться самый маленький элемент, а каждый следующий будет больше предыдущего, называют возрастающим. Если на первом месте будет самый большой элемент, а каждый следующий будет меньше, то такой порядок называют убывающим. Часто среди элементов сортируемой последовательности могут оказаться равные по значению элементы. В этом случае принято говорить о порядке неубывания (невозрастания). В общем случае элементы могут быть не равны по значению, но считаться равными относительно функции сравнения (пример 18.2). Сортировка массива — расположение его элементов в некотором заданном порядке. В отсортированном массиве поиск элемента можно осуществлять, не просматривая весь массив. Например, в случае сортировки в порядке возрастания минимальный элемент массива всегда будет находиться на первом месте. Задача сортировки, как и любая другая задача, может решаться множеством способов, каждый из которых имеет как достоинства, так и недостатки. На сегодняшний день известно более десятка различных алгоритмов сортировки и их модификаций. Выбор алгоритма сортировки определяется особенностями решаемой задачи. Алгоритм сортировки — алгоритм для упорядочения элементов в списке. В случае, когда элемент списка имеет несколько полей, поле, служащее критерием порядка, называется ключом сортировки. При выборе метода сортировки необходимо учитывать следующие моменты: объем требуемой памяти и скорость работы. При сортировке массива желательно использовать как можно меньше дополнительной памяти, поэтому обычно рассматриваются алгоритмы, которые упорядочивают массив перестановками его элементов (без использования еще одного массива). Оценить скорость работы метода сортировки можно, оценив количество требуемых операций сравнения и (или) операций перестановок элементов. Ниже рассматриваются методы сортировки линейного массива по возрастанию (неубыванию). Сортировка по убыванию (невозрастанию) производится аналогично. Сортировка с использованием функции сравнения будет показана в конце параграфа. |
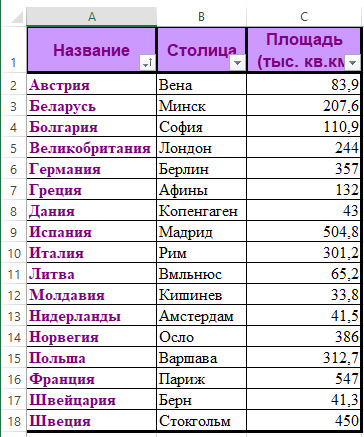
Пример 18.1. Сортировка в электронной таблице. Функцией сравнения в первом случае будет функция, сравнивающая строки лексикографически. Во втором случае сравниваются числовые значения. Первые прототипы современных методов сортировки появились уже в XIX в., когда были изобретены сортировочные машины. Первая такая машина была изобретена Германом Холлеритом (1860–1929). Устройство называлось табулятор, патент на который был получен в 1884 г. Затем в течение пяти лет Г. Холлерит запатентовал перфоратор, сортировку и перфокарту. Табулятор использовался для обработки данных переписи населения в США в 1890 г. При работе табулятор размещал перфокарты по 26 ячейкам «сортировального ящика» (слева) в зависимости от того, d каком месте перфокарты было сделано отверстие. Машина позволяла обрабатывать до 80 перфокарт за час. Созданная Г. Холлеритом в 1896 г. фирма Tabulating Machine Company по производству счетно-аналитических машин со временем слилась с другими компаниями в одну, которая с 1924 г. называется International Business Machines (IBM). До 1921 г. Холлерит оставался консультантом этой фирмы. Пример 18.2. Пусть элементами последовательности являются натуральные числа. Требуется расположить элементы последовательности так, чтобы в начале стояли четные числа, а затем нечетные. Для сортировки в таком порядке можно, например, сравнивать остатки от деления числа на 2. В этом случае четное число (остаток 0) меньше нечетного (остаток 1). Любые два четных числа так же, как и любые два нечетных числа, будут равны относительно функции сравнения. Работа сортировальной машины Г. Холлерита основывалась на методах поразрядной сортировки. Другие известные методы сортировок появились с развитием ЭВМ. По некоторым источникам[1], именно программа сортировки стала первой программой для вычислительных машин. Некоторые конструкторы ЭВМ, в частности разработчики EDVAC, называли задачу сортировки данных наиболее характерной нечисловой задачей для вычислительных машин. В 1945 г. Джон фон Нейман для тестирования ряда команд для EDVAC разработал программы сортировки методом слияния. В том же году немецкий инженер Конрад Цузе разработал программу для сортировки методом простых вставок. В 1959 г. был разработан метод Шелла, в 1962 г. появился алгоритм быстрой сортировки Хоара. Возникшие позже алгоритмы во многом являлись вариациями уже известных методов. Одной из последних разработок является алгоритм Timsort — гибридный алгоритм сортировки, сочетающий сортировку вставками и сортировку слиянием. Опубликован в 2002 г. Тимом Петерсом (американский разработчик ПО, внес большой вклад в язык программирования Python). В настоящее время Timsort является стандартным алгоритмом сортировки в Python и др. Основная идея алгоритма в том, что в реальном мире сортируемые массивы данных часто содержат в себе упорядоченные подмассивы. На таких данных Timsort существенно быстрее многих алгоритмов сортировки.[1] Дональд Е. Кнут. Искусство программирования. Т. 3. Сортировка и поиск. М: ООО «И.Д. Вильямс», 2018. – 832 с. |
18.2. Сортировка выбором
|
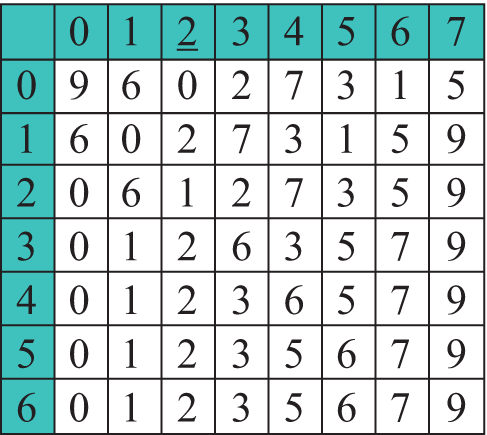
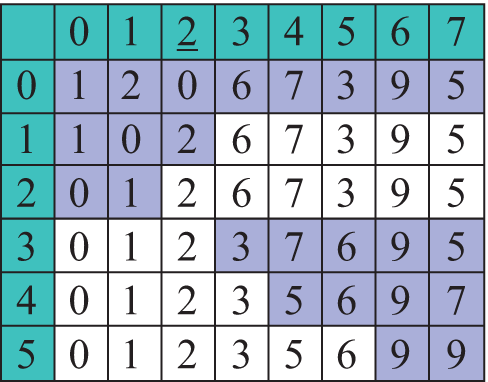
Давайте представим, что перед нами поставлена задача расставить N чисел по возрастанию. Как бы мы ее решали? Наверное, пришлось бы сначала найти минимальное из всех чисел и поставить его на первое место в последовательности. Затем из еще неотсортированных элементов надо было бы опять выбрать минимальный элемент и поставить его после уже отсортированной части и т. д. (пример 18.3) Рассмотрим работу данного метода на массиве a = {9, 6, 0, 2, 7, 3, 1, 5}. Минимальный элемент на каждом шаге подчеркнут (пример 18.4). Цветом выделен тот элемент, который на текущем шаге меняется местами с минимальным. Примененный метод называется сортировкой выбором. Название метода определяется тем, что на каждом шаге мы находим (выбираем) минимальный элемент из еще неотсортированной части массива (пример 18.5). Формальное описание алгоритма. На i-м шаге (i = 0, …, n - 1) выполняем: 1. Выбираем из элементов с индексами от i до n–1 минимальный. Посчитаем количество сравнений, которые пришлось сделать для упорядочения массива. На первом шаге для нахождения максимального элемента необходимо (n – 1) сравнений, на втором — (n – 2), на третьем (n – 3), ..., на последнем шаге — одно сравнение. Найдем сумму: n – 1 + n – 2 + n – 3 ... + 1 = |
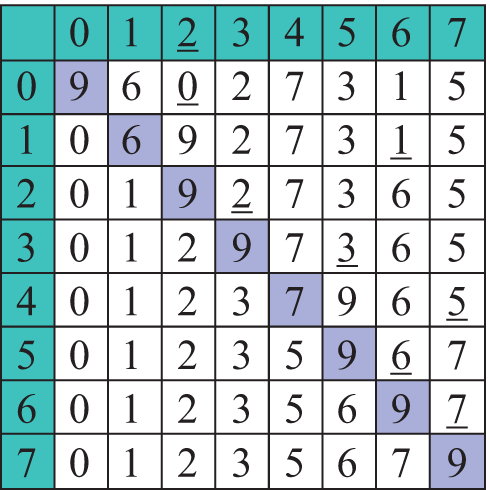
Пример 18.3. Демонстрация сортировки чисел на примере детской игрушки, в которой нужно выбирать и расставлять числа по своим местам: Пример 18.4. Сортировка массива методом выбора: Пример 18.5. Программа алгоритма сортировки методом выбора:
Тестирование. Внутренний цикл for является не чем иным, как алгоритмом поиска минимального элемента среди элементов с номерами от k + 1 до n – 1. Сумму количества сравнений можно получить исходя из того, что числа n – 1, n – 2, … 1 образуют арифметическую прогрессию. Сумма элементов этой арифметической прогрессии равна
|
18.3. Сортировка обменом
|
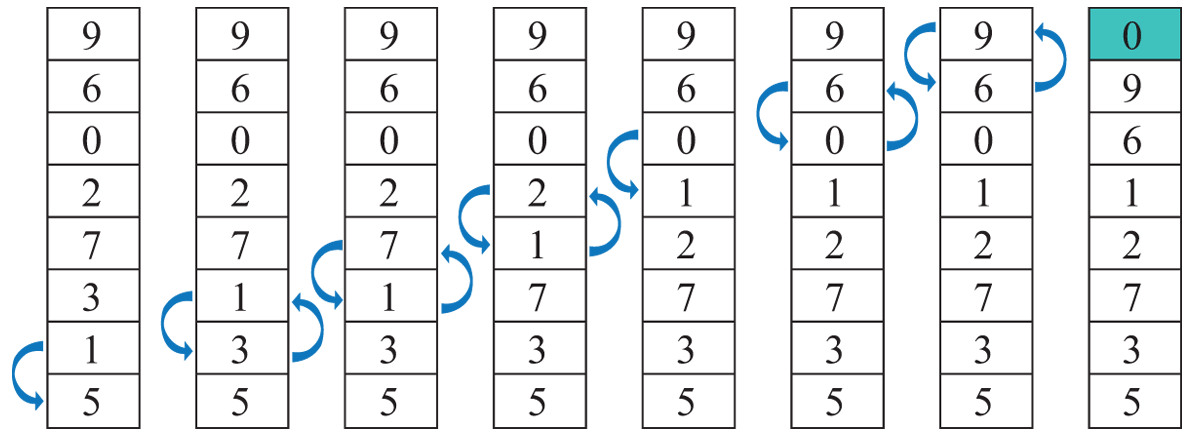
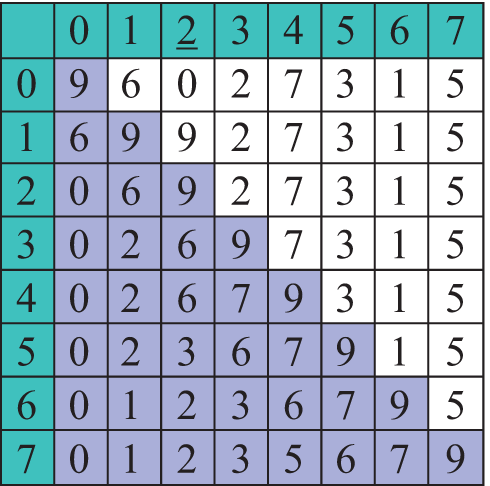
Рассмотрим еще один метод сортировки, который называется сортировка обменом. Название метода определяется тем, что алгоритм основывается на обмене местами двух элементов массива. Меняются местами те два соседних элемента в массиве, которые стоят «не в порядке». Рассмотрим его на примере того же массива a = {9, 6, 0, 2, 7, 3, 1, 5} (пример 18.6). Цветом выделен тот элемент, правее которого просматривать массив нет необходимости, поскольку элементы, стоящие там, уже отсортированы. Формальное описание алгоритма. На i-м шаге (i = 1, …, n – 1) выполняем: 1. Сравниваем первые два элемента. Если первый больше второго, то меняем их местами. 2. Затем сравниваем второй и третий, третий и четвертый, ..., i и i + 1, при необходимости меняя их местами. 3. После первого шага самый большой элемент массива перемещается на последнее место. Массив будет отсортирован после просмотра, в котором участвуют только первый и второй элементы. Фрагмент программы, содержащий алгоритм сортировки обменом, приведен в примере 18.7. Число сравнений в данном алгоритме, как и в алгоритме сортировки выбором, равно При каждом сравнении возможна перестановка двух элементов в массиве. Поэтому количество перестановок (в худшем случае) будет равно количеству сравнений, т. е. порядка n2 операций. На последних двух проходах в примере 18.6 массив не менялся. Заметим, что если на каком-то шаге алгоритма элементы массива уже упорядочены, то при последующих проходах по массиву перестановки больше выполняться не будут. Следовательно, как только количество выполненных на последнем проходе перестановок станет равным 0, то алгоритм можно заканчивать (пример 18.8). Если проанализировать сортировку обменом, то можно заметить, что самое маленькое число занимает свое место за один проход по массиву, а самое большое перемещается по направлению к своему месту на одну позицию при каждом проходе. Это наводит на мысль чередовать направление проходов. Такая сортировка называется шейкер-сортировкой (шейкерная сортировка, сортировка перемешиванием, коктейльная сортировка). Рассмотрим ее работу на том же массиве а = {9, 6 0, 2, 7, 3, 1, 5} (примеры 18.9, 18.10). Все эти улучшения сокращают количество операций сравнения для частных случаев, однако при неблагоприятной начальной расстановке элементов массива (подумайте, какой именно?) приходится проделать порядка n2 операций сравнения и перестановок. Кроме того, такие модификации усложняют код программы. |
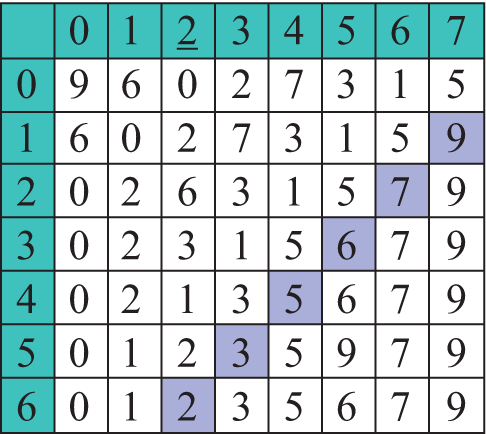
Пример 18.6. Сортировка массива методом обмена: Алгоритм сортировки обменом часто называют «пузырьковой сортировкой» или сортировкой «методом пузырька» (BubbleSort). Название метода происходит из следующего: на каждом шаге самый «легкий» элемент поднимается до своего места («всплывает»). Для этого нужно просматривать элементы снизу вверх (с конца массива). Берем пару соседних элементов и, в случае если они стоят «не в порядке», меняем их местами. Первый проход по массиву: Вместо поднятия самого «легкого» элемента можно «топить» самый «тяжелый». В этом случае элементы просматриваются сначала (как в примере 18.6). Пример 18.7. Фрагмент программы сортировки методом обмена. Ввод и вывод такой, как в примере 18.5.
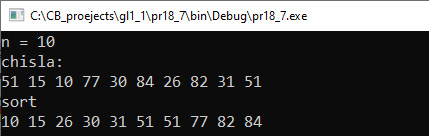
Тестирование. Пример 18.8. Фрагмент программы сортировки методом обмена с остановкой после того, когда обмены больше не происходят.
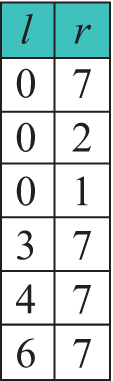
В приведенном фрагменте переменная p логического типа используется для определения, были перестановки или нет, а переменная k — для хранения индекса последнего обмена. Переменная r является границей, на которой заканчивается просмотр. Пример 18.9. Сортировка массива шейкерной сортировкой (l — левая граница просмотра, r — правая): Пример 18.10. Фрагмент программы шейкер-сортировки.
|
18.4. Сортировка простыми вставками
|
Будем просматривать элементы массива a, начиная со второго. Каждый новый элемент a[i] будем вставлять на подходящее место в уже упорядоченную часть массива a[1], ..., a[i–1]. Место вставки определяется путем сравнения элемента a[i] с упорядоченными элементами a[1], ..., a[i–1]. Такой метод сортировки называется сортировкой простыми вставками. Он также требует порядка n2 операций сравнения и столько же перестановок элементов в массиве. Рассмотрим ее работу на массиве а = {9, 6 0, 2, 7, 3, 1, 5} (примеры 18.11). Цветом выделены элементы уже отсортированной части. Формальное описание алгоритма. На i-м шаге (i = 1, …, n – 1) выполняем: 1. Берем первый элемент в неотсортированной части массива. Фрагмент программы, содержащий алгоритм сортировки простыми вставками, приведен в примере 18.12. Алгоритм сортировки, похожий на сортировку вставками, в котором перед вставкой элемента на нужное место происходит серия обменов, как в сортировке пузырьком, называют «гномьей сортировкой». Название происходит от предполагаемого поведения садовых гномов при сортировке линии садовых горшков. Особенностью данного метода является то, что он записывается в один цикл (пример 18.13). Однако количество сравнений и перестановок в худшем случае порядка n2 операций. |
Пример 18.11. Сортировка массива методом простых вставок: Пример 18.12. Фрагмент программы сортировки простыми вставками.
В 2000 г. в научном издании Newsletter университета Глазго был опубликован алгоритм под названием «Глупая сортировка»1. Автор — Хамид Сарбази-Асад (Hamid Sarbazi-Azad). Чуть позже голландский ученый Дик Грун (Dick Grune) исследовал метод подробнее и переименовал его в «Гномью сортировку». Под этим именем алгоритм сейчас и известен. «Гномья сортировка» основана на технике, используемой обычным голландским садовым гномом (нидерл. tuinkabouter). Это метод, которым садовый гном сортирует линию цветочных горшков. По существу, он смотрит на следующий и предыдущий садовые горшки: если они в правильном порядке, он шагает на один горшок вперед, иначе меняет их местами и шагает на один горшок назад. Граничные условия: если нет предыдущего горшка, он шагает вперед; если нет следующего горшка, он закончил. Пример 18.13. Фрагмент программы «гномьей сортировки».
[1] Глупой сортировкой обычно называют другой алгоритм: http://algolab.valemak.com/stupid. |
18.5. Быстрая сортировка
|
Рассмотрим еще один алгоритм сортировки, который является существенным улучшением алгоритма сортировки обменом. Сортировка обменом является одним из самых неэффективных алгоритмов сортировки. Однако усовершенствованный алгоритм позволяет получить результат намного быстрее, поэтому, его изобретатель Чарльз Хоар назвал этот алгоритм быстрой сортировкой (quicksort). Высокая производительность достигается за счет того, что происходит обмен элементов на больших расстояниях. В массиве выбирается некоторый элемент, называемый опорным. Для остальных элементов производятся перестановки таким образом, чтобы слева от опорного находились элементы не больше его, а справа — не меньше. Тем самым массив разбивается на две части:
В дальнейшем для каждой части действия повторяются. Следует заметить, что конечная позиция опорного элемента необязательно совпадает с его позицией до перестановок элементов. Рассмотрим ее работу на том же массиве а = {9, 6, 0, 2, 7, 3, 1, 5} (пример 18.14). Формальное описание алгоритма: 1. Заведем два указателя: левый и правый, которые позволят перемещаться по элементам массива с начала и с конца. 2. В качестве опорного элемента выберем элемент, стоящий на среднем месте. 3. Слева от опорного элемента найдем не меньший, а справа — не больший, чем опорный, и поменяем их местами. 4. Обмен элементов производим, пока указатель из левой части не станет больше указателя из правой части. 5. Рекурсивно обрабатываем 2 части массива: от начала до значения правого указателя и от значения левого указателя до конца. Рекурсивная функция быстрой сортировки приведена в примере 18.15. В худшем случае алгоритм требует порядка n2 операций сравнения и столько же перестановок элементов в массиве. Однако такие случаи встречаются нечасто (пример 18.16). В среднем, если при каждом рекурсивном вызове массив делится на две почти равные части, то количество требуемых операций будет порядка nk, где значение k определяется из равенства 2k = n. Значение k также определяет размер дополнительной памяти для хранения стека рекурсивных вызовов. |
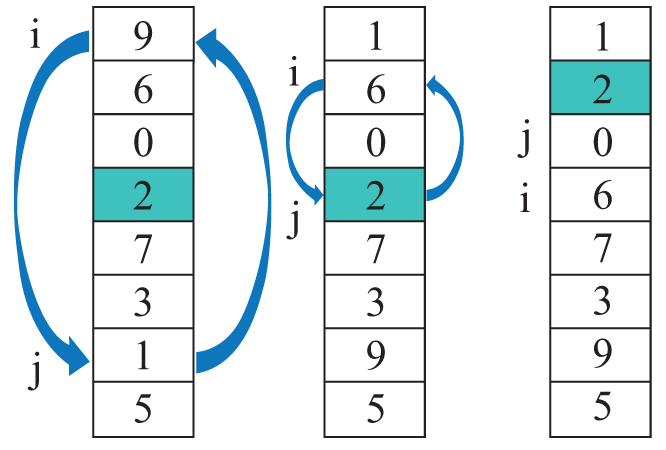
Пример 18.14. Быстрая сортировка. Первый проход по массиву. Переменные i и j — индексы элементов, подлежащих обмену. Сначала i = l = 0, j = r = 7 (переменные l и r — левая и правая границы обрабатываемой части массива). В конце i = 3, j = 2 (i > j), поэтому обмены больше не производятся. Дальше функция по отдельности работает на подмассивах c границами [0, 2] и [3,7]. Дальнейшие этапы работы алгоритма: Пример 18.15. Функция быстрой сортировки.
В ранних реализациях быстрой сортировки, как правило, опорным выбирался первый элемент. Такой выбор снижал производительность на отсортированных массивах. Для улучшения эффективности может выбираться средний, случайный элемент или (для больших массивов) медиана[1] первого, среднего и последнего элементов. Пример 18.16. Примеры ситуаций, когда быстрая сортировка не эффективна:
Рекурсивные вызовы являются затратными операциями, и для небольших массивов их количество будет близким к количеству элементов. Поэтому в случае небольших объемов данных используют нерекурсивные методы сортировки, например сортировку вставками или выбором. *В математике для определения числа k(2k = n) пользуются функцией log[2]. Алгоритм быстрой сортировки в среднем использует порядка nlogn сравнений и обменов[3], а также порядка дополнительной памяти.[1] Медианой трех различных значений будет то, которое не равно ни минимальному, ни максимальному. Например, для значений 3, 100 и 25 медианой будет 25. [2] Если 2k = n, то log2n = k. [3] Кормен, Т. Алгоритмы: построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн., 3-е издание. — М.: «Вильямс», 2013. |
18.6. Использование функции сравнения
|
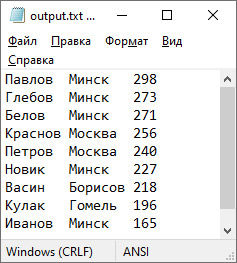
Все сортировки, разобранные выше, позволяли упорядочить элементы массива по возрастанию. Если в алгоритме заменить сравнение элементов на сравнение значений функции от этих элементов, то сортировки могут быть разнообразными. Функцию для сравнения двух объектов называют компаратором (от англ. compare — сравнить). Функция-компаратор зависит от двух параметров и возвращает логическое значение. Тип параметров функции должен совпадать с типом элементов в массиве. Функция должна возвращать знание true, для двух значений, которые находятся «в порядке» и false в противном случае. Пример 18.17. Дан линейный массив из целых чисел. Написать программу сортировки массива так, чтобы все четные числа стояли в начале массива, а нечетные — в конце. Данные сгенерировать случайным образом. Этапы выполнения задания I. Исходные данные: переменные n — количество чисел в массиве, a — массив. II. Результат: отсортированный массив а. III. Алгоритм решения задачи. 1. Ввод исходных данных. Элементы массива сгенерированы случайным образом. IV. Описание переменных: n – int, a – vector<int>. Для решения этой задачи выбор алгоритма сортировки обменом не является оптимальным, поскольку он потребует порядка n2 операций сравнения и обмена. Пример необходим для того, чтобы показать использование функции-компаратора. Для получения оптимального решения можно исходить из того факта, что все числа относительно остатка при делении на 2 бывают всего двух категорий (четные и нечетные), и для их сортировки достаточно всего одного прохода по массиву. Это можно сделать по аналогии с алгоритмом быстрой сортировки с помощью двух указателей: слева ищем первый нечетный, а справа — последний четный и меняем их местами (пример 18.18). Пример 18.19. Дан линейный массив из слов. Написать программу сортировки массива так, чтобы слова располагались в порядке убывания количества букв «а» в слове. Данные прочитать из файла. Этапы выполнения задания I. Исходные данные: переменные n — количество слов в массиве, a — массив. II. Результат: отсортированный массив а. III. Алгоритм решения задачи. 1. Ввод исходных данных.. IV. Описание переменных: n – int, a – vector<string>. Пример 18.20. В текстовом файле input.txt хранится информация о студентах. Для каждого студента указана его фамилия, город, из которого он приехал, и три числа — баллы за ЦТ, с которыми он поступил в вуз. Отсортировать список студентов в порядке убывания суммарного балла за ЦТ. Вывести фамилию, город и суммарный балл. Этапы выполнения задания I. Исходные данные: переменные n — количество записей о студентах, a — массив структур. II. Результат: отсортированный массив а. III. Алгоритм решения задачи. 1. Ввод исходных данных. |
Компаратор — это отношение порядка. Как функция он должен удовлетворять аксиомам отношения порядка:
V. Программа:
VI. Тестирование. Пример 18.18. Фрагмент программы:
V. Программа:
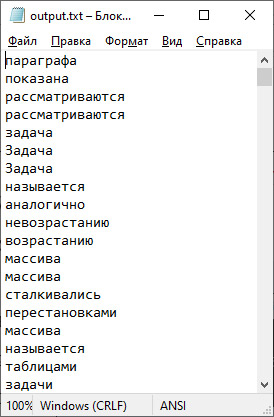
V. Тестирование. В текстовый файл записаны слова из пункта 18.1. V. Фрагмент программы (функцию vvod и подключаемые библиотеки см. пример 17.8):
VI. Тестирование. Используется текстовый файл из примера 17.8. |
Вопросы к параграфу
 |
1. На каких принципах основана сортировка выбором? 2. На каких принципах основана сортировка обменом? 3. В чем суть сортировки простыми вставками? 4. За какое количество операций сравнения будет отсортирован массив, если применять сортировку обменом? 5. Сколько перестановок будет сделано для упорядочения массива, если применять сортировку выбором? 6. В чем преимущество алгоритма быстрой сортировки? 7. Какие недостатки есть у алгоритма быстрой сортировки? |
Упражнения



1. Дан линейный массив (вектор) из целых чисел. Написать программу сортировки массива. Данные сгенерировать случайным образом.
- Так, чтобы все кратные трем стояли в начале массива, а не кратные в конце.
- В порядке возрастания суммы цифр числа.
- В порядке убывания количества делителей числа.
2. Дан линейный массив (вектор) из слов. Написать программу сортировки массива. Данные читать из файла.
- По количеству букв в слове, в порядке возрастания.
- По количеству согласных букв в слове, в порядке убывания.
- По количеству различных букв в слове, в порядке возрастания.
3. Дан линейный массив (вектор) из структур. Написать программу сортировки массива. Данные читать из файла. Можно использовать файлы, созданные для упражнения 6 после § 17.
1. В файле хранятся: название страны, столица, площадь (тыс. км2) и количество населения (млн чел.).
Беларусь Минск 208 9.41
Россия Москва 17075 143.3
США Вашингтон 9373 310.2
Канада Оттава 9985 34.2
Франция Париж 547 65.4
И т.д.
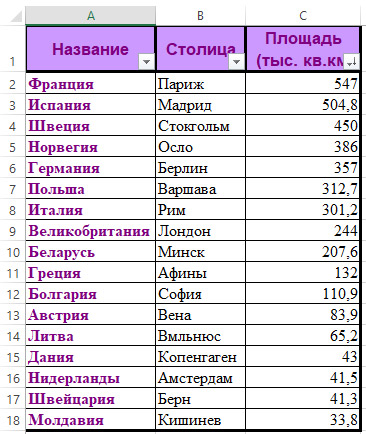
Отсортировать данные в порядке возрастания площади.
2. В файле хранятся: название производителя стиральной машины, ее модель, мощность и максимальная загрузка белья (кг).
Samsung WW65K52E69S 2400 6.5
Bosch WLT24440OE 2300 7
Haier HW70-BP12758S 1900 7
LG F12M7NDS0 1700 6
И т.д.
Отсортировать данные в алфавитном порядке по названию производителя.
3. В файле хранятся: название озера, область в которой расположено, его объем (млн м3), площадь (км2), максимальная глубина (м) и прозрачность(м).
Нарочь Минская 710 79.6 24.8 7.4
Снуды Витебская 107 22 16.5 6.6
Ричи Витебская 131.5 12.9 51.9 5.5
Свитязь Гродненская 7.76 25.2 15 5.2
И т.д.
Отсортировать данные в порядке убывания прозрачности.
4*. Провести исследование методов сортировок (выбором, обменом и вставками). Подготовить отчет в электронных таблицах (можно использовать совместный доступ к таблице). Программы для каждой сортировки скомпилировать в режиме release. Запускать откомпилированные программы из операционной системы, используя файловый менеджер.
Для измерения времени можно использовать int t1 = clock(); из библиотеки ctime, выдает время в миллисекундах. Время замерять до начала работы алгоритма и после окончания работы алгоритма (разница — время работы алгоритма).
Для выполнения работы руководствоваться следующим планом (для каждого алгоритма):
- Сгенерировать текстовый файл из 20 000 целых чисел (диапазон чисел: –10000..10000).
- Измерить и записать время работы программ для полученного файла.
- Сгенерировать текстовый файл из 20 000 целых чисел (диапазон чисел: –100..100).
- Измерить и записать время работы программ.
- Увеличить количество элементов в пунктах 1 и 3 в два раза (до 40 000). Как изменить время выполнения программы?
- Пункты 1—5 выполнить 10 раз.
- Отсортировать в обратном порядке уже отсортированный массив для:
7.1. 20000 целых чисел (диапазон чисел –10000..10000).
7.2. 20000 целых чисел (диапазон чисел –100..100);
7.3. 40000 целых чисел (диапазон чисел –10000..10000;
7.4. 40000 целых чисел (диапазон чисел –100..100).
8. Найти среднее значение времени по всем видам сортировок (от суммы отнять минимальное, максимальное и разделить на 8).
9. Определить минимальное количество элементов, при которых каждая программа будет работать больше 30 секунд.
5*. Определить время работы алгоритма быстрой сортировки для тех же файлов, которые использовались в упражнении 4. Сделать выводы.