§ 7. Понятие вспомогательного алгоритма

7.3. Наибольший общий делитель двух чисел

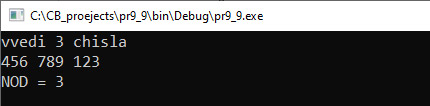
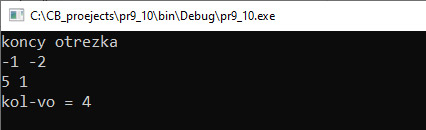
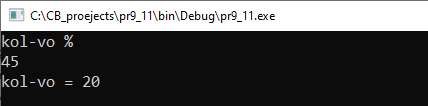
Наибольшим общим делителем (НОД) для двух целых чисел называют наибольший из их общих делителей. Пример: для чисел 42 и 24 наибольший общий делитель равен 6.

Существуют несколько алгоритмов нахождения НОД. На уроках математики вы познакомились со следующим алгоритмом:

1) разложить каждое из чисел на простые множители;

2) выбрать в разложениях общие множители;

3) перемножить выбранные числа;

(Рассмотрим пример 7.7.)

На уроках информатики в 8-м классе вы познакомились с алгоритмом Евклида:

1) из большего числа вычитаем меньшее;

2) если получается 0, то числа равны друг другу и это значение является НОД;

3) если результат вычитания не равен 0, то большее число заменяем на разность большего и меньшего;

4) переходим к пункту 1.

(Рассмотрим пример 7.8.)

Для реализации алгоритма из курса математики понадобится реализация нескольких функций: функция для разложения числа на множители, функция для сравнения двух разложений и отбора одинаковых чисел, функция для перемножения чисел. Кроме того, понадобится дополнительная память, чтобы сохранять разложение чисел. В то же время для нахождения НОД по алгоритму Евклида достаточно одной функции, которая будет работать с двумя переменными.

Пример 7.9. Написать программу вычисления НОД(a, b, c).

Этапы выполнения задания

 I. Исходные данные: a, b и c (три числа).

II. Результат: НОД (a, b, c).

III. Алгоритм решения задачи.

1. Ввод чисел a, b, c.
2. Воспользуемся тем, что НОД (a, b, c)= НОД (НОД (a, b), c). То есть сначала вычислим d = НОД (a, b), а затем f = НОД (d, c). 
3. Для вычисления НОД двух чисел составим функцию gcd[1](x, y), которая вычисляет значение НОД двух чисел по алгоритму Евклида. 
4. Вывод результата.

IV. Описание переменных: a, b, c, d, f – int.

Пример 7.10. На плоскости задан отрезок, концы которого имеют целочисленные координаты. Сколько точек с целочисленными координатами принадлежат этому отрезку? Например, для отрезка с концами (–5; 5) и (4; –1) таких точек будет 4.

Этапы выполнения задания

I. Исходные данные: x1, y1, x2, y2 (координаты концов отрезка).

II. Результат: k — количество точек.

III. Алгоритм решения задачи.

1. Ввод исходных данных. 
2. Точки с целочисленными координатами разделят отрезок на части. Количество таких частей будет равно 
НОД space open parentheses open vertical bar x subscript 1 space minus space x subscript 2 close vertical bar comma space space open vertical bar y subscript 1 space minus space y subscript 2 close vertical bar close parentheses.
3. Количество точек на одну больше, чем количество частей. 
4. Для вычисления НОД двух чисел составим функцию gcd(x, y), которая вычисляет значение НОД двух чисел по алгоритму Евклида. 
5. Вывод результата.

IV. Описание переменных: x1, y1, x2, y2, k – int.

Пример 7.11. Параллель десятых классов написала контрольную работу. В результате ровно a% учащихся получили отметки от 7 до 10, остальные — от 1 до 6. Какое минимальное количество учащихся должно быть в параллели десятых классов для того, чтобы мог получиться такой результат?

Этапы выполнения задания

I. Исходные данные: а — количество процентов успешных работ.

II. Результат: k — количество учащихся.

III. Алгоритм решения задачи.

1. Ввод исходных данных. 
2. Если а — количество процентов работ, выполненных на 7—10, то количество процентов остальных работ:
b = 100 – а.
3. Минимальное количество: k space equals space fraction numerator 100 over denominator НОД left parenthesis straight а comma space straight b right parenthesis end fraction.
4. Для вычисления НОД двух чисел составим функцию gcd (x, y), которая вычисляет значение НОД двух чисел по алгоритму Евклида.
5. Вывод результата.

IV. Описание переменных: a, b, k — int.

[1] gcd — от англ. greatest common divisor (наибольший общий делитель).

Пример 7.7. Нахождение наибольшего общего делителя для чисел 42 и 24:

1)  begin mathsize 14px style 42 space equals space 2 space times space 3 space times space 7 comma space space space 24 space equals space 2 space times space 2 space times space 3 colon end style 

2)  общие множители: 2 и 3;

3)  begin mathsize 14px style НОД space equals space 2 space times space 3 space equals space 6. end style

Пример 7.8. Алгоритм Евклида для чисел 42 и 24:

a

b
42 24
18 (42−24) 24
18 6 (24−18)
12 (18−6) 6
6 (12−6) 6

Анализируя действия, выполняемые в алгоритме Евклида, можно заметить, что можно заменить большее число на остаток от деления большего числа на меньшее. Корректность данного факта следует из следующего утверждения: если a = b · q + r, то НОД(a, b) = НОД(b, r). При такой организации вычислений алгоритм закончит свою работу, когда одно из чисел станет равным нулю. Тогда значение НОД будет равно другому числу, поскольку НОД(r, 0) = r для любого ненулевого r (т. к. 0 делится на любое целое число).

Пример 7.9.

V. Программа:

#include <iostream>

 

using namespace std;

 

int gcd (int x, int y)

{

  while (y != x){

    if (x > y)

      x -= y;

    else

      y -= x;

  }

  return x;

}

int main()

{

  int a, b, c;

  cout << "vvedi 3 chisla" << endl;

  cin >> a >> b >> c;

  int d = gcd(a, b);

  int f = gcd(d, c);

  cout << "NOD = " << f << endl;

  return 0;

}

 VI. Тестирование.

Для компилятора MinGW, который устанавливается вместе с Code::Bloks, реализована функция __gcd(n, m). Она находит НОД двух чисел. Использовать эту функцию можно после подключения библиотеки algorithm.

Пример 7.10.

V. Программа:

#include <iostream>

#include <cmath>

 

using namespace std;

 

int gcd (int x, int y)

{

  while (x && y){

    if (x > y)

      x %= y;

    else

      y %= x;

  }

  return (x + y);

}

int main()

{

  int x1, y1, x2, y2;

  cout << "koncy otrezka" << endl;

  cin >> x1 >> y1 >> x2 >> y2;

  int a = abs(x1 - x2);

  int b = abs(y1 - y2);

  int k = gcd(a, b) + 1;

  cout << "kol-vo = " << k;

  return 0;

}

VI. Тестирование.

Пример 7.11.

V. Программа:

#include <iostream>

 

using namespace std;

 

int gcd (int x, int y)

{

  while (x && y){

    x %= y;

    swap(x, y);

  }

  return (x + y);

}

int main()

{

  int a;

  cout << "kol-vo %" << endl;

  cin >> a;

  int b = 100 - a;

  int k = 100 / gcd(a, b);

  cout << "kol-vo = " << k << endl;

  return 0;

}

VI. Тестирование.

В данной реализации алгоритма Евклида использовано следующее свойство: НОД (x, y) = НОД (y, x). Функция swap(x, y) меняет местами значения переменных x и y.