Печатать книгуПечатать книгу

§ 7. Понятие вспомогательного алгоритма

Сайт: Профильное обучение
Курс: Информатика. 10 класс (Повышенный уровень)
Книга: § 7. Понятие вспомогательного алгоритма
Напечатано:: Гость
Дата: Суббота, 4 Май 2024, 14:19

Оглавление

7.1. Вспомогательные алгоритмы

Вспомогательный алгоритм — алгоритм, который можно использовать в других алгоритмах, указав его имя и, если необходимо, значения параметров. Вспомогательный алгоритм, записанный на языке программирования, называют подпрограммой.

Основные преимущества использования подпрограмм:

1. Разбиение комплексной программной задачи на простые шаги (декомпозиция). Это позволяет распределить решение одной задачи между различными людьми. 
2. Уменьшение повторяющегося кода. 
3. Многократное использование кода в других программах, в том числе и другими программистами. 
4. Сокрытие деталей реализации от пользователей подпрограммы.

Подпрограммы, которые используются часто, объединяют в библиотеки. Большинство языков программирования позволяют не только использовать готовые подпрограммы, но и писать свои. В языке C++ подпрограммы оформляются в виде функций. Вам уже приходилось использовать различные функции, например из библиотеки cmath.

Перед тем как использовать функцию, ее нужно описать. Описание функции включает объявление и определение функции.

Объявление функции (пример 7.1) включает в себя заголовок функции, заканчивающийся точкой с запятой и включающий:

  • имя функции f_N;
  • перечень формальных параметров с их типами
    (type a_1, type a_2,… , type a_N);
  • тип возвращаемого значения
    r_type:    r _type f_N (type a_1, type a_2, ..., type a_N);

Функции могут быть с параметрами или без параметров. Если функция не имеет параметров, то наличие круглых скобок после имени функции обязательно.

Определение функции состоит из заголовка функции (без точки с запятой) и тела функции, заключенного в фигурные скобки. В нем содержатся команды языка, реализующие вспомогательный алгоритм (пример 7.2).

Главная программа на С++ также реализована в виде функции. Эта функция всегда имеет имя main. Тип результата и наличие параметров этой функции может быть различными для различных сред программирования. В среде Code::Blocks функция main() имеет тип int и не имеет параметров.

Обычно объявление и описание подпрограмм размещают до функции main(). Если для решения задачи необходимо реализовать несколько функций, то нужно помнить о том, что функция должна быть объявлена до того, как она будет вызвана.

При вызове функции (пример 7.3) указывается ее имя и параметры, необходимые для вычислений. Эти параметры называют фактическими параметрами.

В описании функции задается список формальных параметров. Каждый параметр, описанный в этом списке, является локальным по отношению к описываемой функции, т. е. на него можно ссылаться по его имени из данной подпрограммы, но не из основной программы или другой функции.

Переменные, значения которых должны быть известны во всех функциях, являются глобальными и описываются до описания функций. Если переменная описана между описаниями функций, то ее значение будет глобальным для всех функций, описанных ниже, но неизвестным для функций, описанных выше. 

Необходимость оптимизации программ по объему занимаемой памяти привела к появлению подпрограмм. Подпрограммы позволили не повторять в программе идентичные блоки кода, а описывать их однократно и вызывать по мере необходимости.

Использование подпрограмм позволяет повысить надежность кода программы. Подпрограммы обычно имеют небольшой размер, поэтому найти и исправить в них ошибки проще, нежели в большой программе.

Использование подпрограмм гарантирует относительную автономность модификации программы: если нужно что-либо изменить в программе, переделывать придется не всю программу, а только некоторые подпрограммы.

Пример 7.1. Объявление функций.

int kol_cifr (int n);
double plos_treug(double a, double h);

double pi();

Пример 7.2. Определение функции.

int kol_cifr (int n)

{

    int k = 0;

    while (n >0 ) {

        n /= 10;

        k++;

    }

    return k;

}

 

double plos_treug(double a, double h)

{

    double s = a * h / 2;

    return s;

}

 

double pi()

{

    return acos(-1.);

}

В среде Dev-C++ функция main может иметь аргументы:

В среде Microsoft Visual Studio тип возвращаемого значения у функции main может быть void:

Пример 7.3. Вызов функции.

int k = kol_cifr (12345);

double s_kv = 2 * plos_treug(a1, h1);

cout << pi();

В С++ объявление и определение функции может быть в разных местах. Объявление размещают до функции main, а определение после нее.

#include <iostream>

#include <cmath>

 

using namespace std;

 

int kol_cifr (int n);

 

double plos_treug(double a, double h);

 

double pi();

 

int main()

{

  int k = kol_cifr (12345);

  double a1 = 5, h1 = 3.2;

  double s_kv = 2 * plos_treug(a1, h1);

  cout << pi() << endl;

  ///...

  return 0;

}

 

int kol_cifr (int n)

{

  int k = 0;

  while (n >0 ) {

    n /= 10;

    k++;

  }

  return k;

}

 

double plos_treug(double a, double h)

{

  double s = a * h / 2;

  return s;

}

 

double pi()

{

  return acos(-1.);

}

7.2. Функции, возвращающие числовой результат

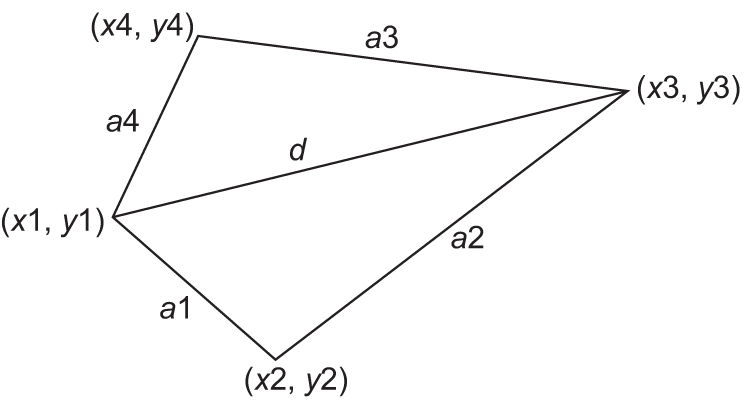
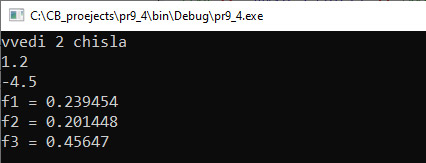
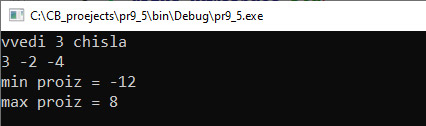
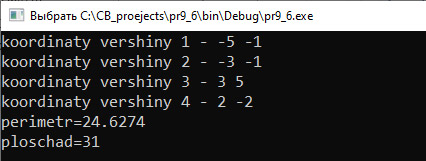
Большинство функций из библиотеки cmath, которые использовались ранее, возвращают в качестве результата число.

Для того чтобы функция могла возвращать значение, используется оператор return, после которого указывается возвращаемое значение. Возвращаемым значением может быть константа (значение 0 у функции main), переменная (в примере 7.2 это функции plos_treug и kol_cifr) или выражение (функция pi()в примере 7.2).

Тип возвращаемого значения должен совпадать с типом результата в описании функции[1].

Пример 7.4. Для функции begin mathsize 16px style f left parenthesis x right parenthesis space equals space fraction numerator square root of open vertical bar x space minus space 2 close vertical bar end root over denominator x squared space plus space 3 end fraction end style вычислить и вывести: f open parentheses – 2.4 close parentheses comma space space f left parenthesis y right parenthesis comma space space f left parenthesis f left parenthesis 3.7 space asterisk times space z right parenthesis right parenthesis. Значения переменных y и z вводятся.

Этапы выполнения задания

I.   Исходные данные: числа y, z.

II. Результат: f1, f2, f3 — значения функции для указанных значений аргументов.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Опишем функцию, вычисляющую значение f по указанной формуле.
3. Вычислим значение функции для указанных аргументов. 
4. Вывод значений функции.

VI. Описание переменных: y, z, f1, f2, f3 – double.

Рассмотрим, как выполняется программа. При вызове функции значение фактического параметра передается формальному и происходит вычисление с этим значением.

В первом случае фактическим параметром является константа –2.4. Поэтому переменная x получит значение –2.4, переменная t 1 space equals space square root of open vertical bar – 2.4 space – space 2 close vertical bar end root space almost equal to space 2.097 comma переменная t 2 space equals space x squared space plus space 3 space equals space 8.76. Функция вернет значение fraction numerator 2.097 over denominator 8.76 end fraction space almost equal to space 0.239 comma которое и будет присвоено переменной f.

Во втором случае переменной x будет передано значение переменной y, которое ввели с клавиатуры, и затем будут выполнены вычисления.

В третьем случае вызов функции осуществляется дважды: сначала для значения 3.7 * z, а затем аргументом функции станет значение f(3.7 * z).

Пример 7.5. Даны три числа. Найти попарные произведения этих чисел. Написать программу, которая вычислит минимальное и максимальное из этих значений.

Этапы выполнения задания

I. Исходные данные: числа x, y, z.

II.  Результат: minpr, maxpr (минимальное и максимальное произведения).

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Опишем функции, вычисляющие минимальное и максимальное значение для двух чисел. 
3. Находим попарные произведения чисел x, y, z. Таких произведений будет три: xy, yz, xz.  
4. Для нахождения минимального значения из трех чисел воспользуемся следующим свойством:
Min(a1, a2, a3) = Min(Min(a1, a2), a3). Максимальное значение находится аналогично.
5. Вывод результатов.

IV.Описание переменных: все переменные в программе имеют тип int.

Пример 7.6. Выпуклый четырехугольник задан координатами своих вершин. Написать программу, которая найдет периметр и площадь четырехугольника. Вычисление длины отрезка и площади треугольника оформить в виде подпрограмм.

Этапы выполнения задания

I. Исходные данные: x1, y1, x2, y2, x3, y3, x4, y4 (координаты вершин).

II. Результат: P и S — периметр и площадь четырехугольника.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Периметр четырехугольника — сумма длин его сторон. Длина стороны — длина отрезка, соединяющего вершины. Вычисление длины отрезка оформляем в виде функции dlin.
3. Для вычисления площади проведем диагональ, соединяющую вершины с координатами (x1, y1) и (x3, y3) или (x2, y2) и (x4, y4). Четырехугольник разобьется на два треугольника, сумма площадей которых и даст искомую площадь. Площадь треугольника вычислим по формуле Герона, т. к. для треугольников известны длины сторон. Обозначения вспомогательных переменных — на рисунке.


Вычисление площади треугольника оформляем в виде функции plos.
4. Вывод результата.

IV. Описание переменных: все переменные в программе имеют тип double.

[1] При несовпадении типов происходит попытка преобразования типов. Если это невозможно, то компилятор выдаст ошибку.

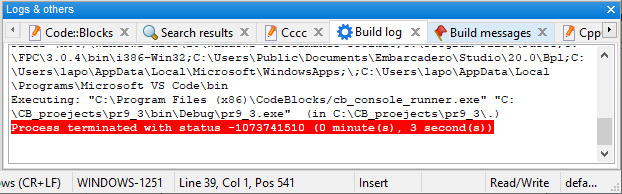
Значение 0, которое возвращает функция main, говорит об отсутствии ошибок при выполнении программы. Это означает, что все команды, которые находятся в программе до этой строки, выполнились успешно. Команда return 0; может быть использована для прерывания работы функции. Никакие команды не могут быть выполнены после нее.

Об успешном выполнении программы свидетельствует сообщение «Process terminated with status 0» в окне Build log.

Если работа программы была прервана (например, пользователь закрыл консольное окно до того, как программа закончила работу), то в этом окне будет сообщение об ошибке: «Process terminated with status −1073741510»

Пример 7.4.

 V. Программа:

#include <iostream>

#include <cmath>

 

using namespace std;

 

double f(double x)

{

  double t1 = sqrt(abs(x - 2));

  double t2 = x * x + 3;

  return t1 / t2;

}

 

int main()

{

  double y, z;

  cout << "vvedi 2 chisla" << endl;

  cin >> y >> z;

  double f1 = f(-2.4);

  cout << "f1 = " << f1 << endl;

  double f2 = f(y);

  cout << "f2 = " << f2 << endl;

  double f3 = f( f(3.7 * z) );

  cout << "f3 = " << f3 << endl;

  return 0;

}

 VI.  Тестирование.

VII. Анализ результата. Проверить правильность вычислений можно с помощью калькулятора.

Пример 7.5.

V. Программа:

#include <iostream>

 

using namespace std;

 

int Max(int c,int d)

{

  if (c > d)

    return c;

  else

    return d;

}

 

int Min(int c, int d)

{

  if (c < d)

    return c;

  else

    return d;

}

 

int main()

{

  int x, y, z;

  cout << "vvedi 3 chisla" << endl;

  cin >> x >> y >> z;

  int a1 = x * y;

  int a2 = y * z;

  int a3 = x * z;

  int s = Min(a1, a2);

  int minpr = Min(s, a3);

  cout << "min proiz = " << minpr << endl;

  s = Max(a1, a2);

  int maxpr = Max(s, a3);

  cout << "max proiz = " << maxpr << endl;

  return 0;

}

 VI. Тестирование.

Пример 7.6.

V. Программа:

#include <iostream>

#include <cmath>

 

using namespace std;

 

double dlin(double x, double y, double x0, double y0)

{  

  double d = (x - x0) * (x - x0) + (y - y0) * (y - y0);

  return sqrt(d);

}

double plos(double a, double b, double c)

{  

  double pr = (a + b + c) / 2;

  double pl = sqrt(pr * (pr - a) * (pr - b) * (pr - c));

  return pl;

}

 

int main()

{

  double x1,y1,x2,y2,x3,y3,x4,y4;

  cout << "koordinaty vershiny 1 - ";

  cin >> x1 >> y1;

  cout << "koordinaty vershiny 2 - ";

  cin >> x2 >> y2;

  cout << "koordinaty vershiny 3 - ";

  cin >> x3 >> y3;

  cout << "koordinaty vershiny 4 - ";

  cin >> x4 >> y4;

  ///стороны и диагональ

  double a1 = dlin(x1, y1, x2, y2);

  double a2 = dlin(x2, y2, x3, y3);

  double a3 = dlin(x3, y3, x4, y4);

  double a4 = dlin(x4, y4, x1, y1);

  double d = dlin(x1, y1, x3, y3);

  ///периметр

  double p = a1 + a2 + a3 + a4;

  ///площадь

  double s1 = plos(a1, a2, d);

  double s2 = plos(a3, a4, d);

  double s = s1 + s2;

  cout << "perimetr=" << p << endl;

  cout << "ploschad=" << s << endl;

  return 0;

}

 VI. Тестирование.

VII. Анализ результата. Обратите внимание на имена переменных в программе. Фактические и формальные параметры принято называть разными именами. 

7.3. Наибольший общий делитель двух чисел

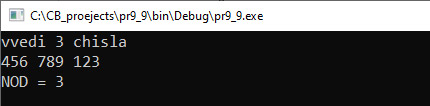
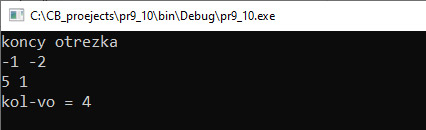
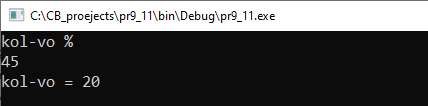
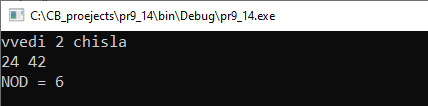
Наибольшим общим делителем (НОД) для двух целых чисел называют наибольший из их общих делителей. Пример: для чисел 42 и 24 наибольший общий делитель равен 6.

Существуют несколько алгоритмов нахождения НОД. На уроках математики вы познакомились со следующим алгоритмом:

1) разложить каждое из чисел на простые множители;

2) выбрать в разложениях общие множители;

3) перемножить выбранные числа;

(Рассмотрим пример 7.7.)

На уроках информатики в 8-м классе вы познакомились с алгоритмом Евклида:

1) из большего числа вычитаем меньшее;

2) если получается 0, то числа равны друг другу и это значение является НОД;

3) если результат вычитания не равен 0, то большее число заменяем на разность большего и меньшего;

4) переходим к пункту 1.

(Рассмотрим пример 7.8.)

Для реализации алгоритма из курса математики понадобится реализация нескольких функций: функция для разложения числа на множители, функция для сравнения двух разложений и отбора одинаковых чисел, функция для перемножения чисел. Кроме того, понадобится дополнительная память, чтобы сохранять разложение чисел. В то же время для нахождения НОД по алгоритму Евклида достаточно одной функции, которая будет работать с двумя переменными.

Пример 7.9. Написать программу вычисления НОД(a, b, c).

Этапы выполнения задания

 I. Исходные данные: a, b и c (три числа).

II. Результат: НОД (a, b, c).

III. Алгоритм решения задачи.

1. Ввод чисел a, b, c.
2. Воспользуемся тем, что НОД (a, b, c)= НОД (НОД (a, b), c). То есть сначала вычислим d = НОД (a, b), а затем f = НОД (d, c). 
3. Для вычисления НОД двух чисел составим функцию gcd[1](x, y), которая вычисляет значение НОД двух чисел по алгоритму Евклида. 
4. Вывод результата.

IV. Описание переменных: a, b, c, d, f – int.

Пример 7.10. На плоскости задан отрезок, концы которого имеют целочисленные координаты. Сколько точек с целочисленными координатами принадлежат этому отрезку? Например, для отрезка с концами (–5; 5) и (4; –1) таких точек будет 4.

Этапы выполнения задания

I. Исходные данные: x1, y1, x2, y2 (координаты концов отрезка).

II. Результат: k — количество точек.

III. Алгоритм решения задачи.

1. Ввод исходных данных. 
2. Точки с целочисленными координатами разделят отрезок на части. Количество таких частей будет равно 
НОД space open parentheses open vertical bar x subscript 1 space minus space x subscript 2 close vertical bar comma space space open vertical bar y subscript 1 space minus space y subscript 2 close vertical bar close parentheses.
3. Количество точек на одну больше, чем количество частей. 
4. Для вычисления НОД двух чисел составим функцию gcd(x, y), которая вычисляет значение НОД двух чисел по алгоритму Евклида. 
5. Вывод результата.

IV. Описание переменных: x1, y1, x2, y2, k – int.

Пример 7.11. Параллель десятых классов написала контрольную работу. В результате ровно a% учащихся получили отметки от 7 до 10, остальные — от 1 до 6. Какое минимальное количество учащихся должно быть в параллели десятых классов для того, чтобы мог получиться такой результат?

Этапы выполнения задания

I. Исходные данные: а — количество процентов успешных работ.

II. Результат: k — количество учащихся.

III. Алгоритм решения задачи.

1. Ввод исходных данных. 
2. Если а — количество процентов работ, выполненных на 7—10, то количество процентов остальных работ:
b = 100 – а.
3. Минимальное количество: k space equals space fraction numerator 100 over denominator НОД left parenthesis straight а comma space straight b right parenthesis end fraction.
4. Для вычисления НОД двух чисел составим функцию gcd (x, y), которая вычисляет значение НОД двух чисел по алгоритму Евклида.
5. Вывод результата.

IV. Описание переменных: a, b, k — int.

[1] gcd — от англ. greatest common divisor (наибольший общий делитель).

Пример 7.7. Нахождение наибольшего общего делителя для чисел 42 и 24:

1)  begin mathsize 14px style 42 space equals space 2 space times space 3 space times space 7 comma space space space 24 space equals space 2 space times space 2 space times space 3 colon end style 

2)  общие множители: 2 и 3;

3)  begin mathsize 14px style НОД space equals space 2 space times space 3 space equals space 6. end style

Пример 7.8. Алгоритм Евклида для чисел 42 и 24:

a

b
42 24
18 (42−24) 24
18 6 (24−18)
12 (18−6) 6
6 (12−6) 6

Анализируя действия, выполняемые в алгоритме Евклида, можно заметить, что можно заменить большее число на остаток от деления большего числа на меньшее. Корректность данного факта следует из следующего утверждения: если a = b · q + r, то НОД(a, b) = НОД(b, r). При такой организации вычислений алгоритм закончит свою работу, когда одно из чисел станет равным нулю. Тогда значение НОД будет равно другому числу, поскольку НОД(r, 0) = r для любого ненулевого r (т. к. 0 делится на любое целое число).

Пример 7.9.

V. Программа:

#include <iostream>

 

using namespace std;

 

int gcd (int x, int y)

{

  while (y != x){

    if (x > y)

      x -= y;

    else

      y -= x;

  }

  return x;

}

int main()

{

  int a, b, c;

  cout << "vvedi 3 chisla" << endl;

  cin >> a >> b >> c;

  int d = gcd(a, b);

  int f = gcd(d, c);

  cout << "NOD = " << f << endl;

  return 0;

}

 VI. Тестирование.

Для компилятора MinGW, который устанавливается вместе с Code::Bloks, реализована функция __gcd(n, m). Она находит НОД двух чисел. Использовать эту функцию можно после подключения библиотеки algorithm.

Пример 7.10.

V. Программа:

#include <iostream>

#include <cmath>

 

using namespace std;

 

int gcd (int x, int y)

{

  while (x && y){

    if (x > y)

      x %= y;

    else

      y %= x;

  }

  return (x + y);

}

int main()

{

  int x1, y1, x2, y2;

  cout << "koncy otrezka" << endl;

  cin >> x1 >> y1 >> x2 >> y2;

  int a = abs(x1 - x2);

  int b = abs(y1 - y2);

  int k = gcd(a, b) + 1;

  cout << "kol-vo = " << k;

  return 0;

}

VI. Тестирование.

Пример 7.11.

V. Программа:

#include <iostream>

 

using namespace std;

 

int gcd (int x, int y)

{

  while (x && y){

    x %= y;

    swap(x, y);

  }

  return (x + y);

}

int main()

{

  int a;

  cout << "kol-vo %" << endl;

  cin >> a;

  int b = 100 - a;

  int k = 100 / gcd(a, b);

  cout << "kol-vo = " << k << endl;

  return 0;

}

VI. Тестирование.

В данной реализации алгоритма Евклида использовано следующее свойство: НОД (x, y) = НОД (y, x). Функция swap(x, y) меняет местами значения переменных x и y.

7.4. Функции, возвращающие логический результат

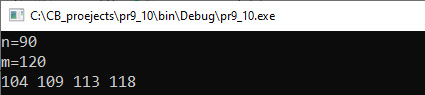
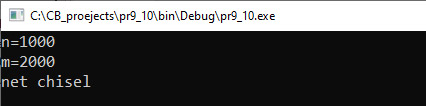
Достаточно часто при решении задач возникает необходимость в проверке различных условий. Если условие не сложное, то можно использовать команду ветвления. Однако на практике условия могут быть достаточно сложными. В этом случае можно описать вспомогательный алгоритм, который выполнит проверку условия и вернет значение true или false в зависимости от того, выполнено условие или нет.

Пример 7.12. Даны два натуральных числа n и m (n < m). Вывести все числа, которые принадлежат отрезку [n; m] и удовлетворяют следующему условию: в числе нечетное количество цифр и сумма цифр числа кратна 5. Предусмотреть случай, когда таких чисел нет. Проверку одного числа оформить в виде подпрограммы.

Этапы выполнения задания

I. Исходные данные: переменные n и m.

II. Результат: числа из промежутка от n до m, удовлетворяющие условию задачи.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Для определения наличия искомых чисел будем использовать логическую переменную p, предварительно задав ей значение p = false.
3. В цикле от n до m проверяем текущее число.

3.1. Для проверки опишем функцию check, которая будет проверять число. Результатом функции будет true или false. 
3.2. Если число удовлетворяет условию, то выведем его. 
3.3. Если вывели число, то изменим значение переменной p на true.
4. Если после окончания цикла значение переменной p осталось false, то выведем сообщение, что искомых чисел на отрезке нет.

IV. Описание переменных: n и m — int, p —  bool.

Пример 7.12.

V. Программа:

#include <iostream>

using namespace std;

 

bool check(int x)

{

  int k = 0, s = 0;

  while (x > 0){

    //сумма цифр числа

    s += x % 10;

    //количество цифр числа

    k++;

    x /= 10;

  }

  if (k % 2 !=0 && s % 5 == 0)

    return true;

  else

    return false;

}

int main()

{

  int m, n, i;

  cout << "n=";

  cin >> n;

  cout << "m=";

  cin >> m;

  bool p = false;

  for (int i = n; i <= m; i++)

    if (check(i)){

      cout << i << " ";

      p = true;

    }

  if (!p)

    cout << "net chisel" << endl;

  return 0;

}

 

VI. Тестирование.

Поскольку функция для проверки результата имеет тип bool и условие (k % 2 != 0 && s % 5 == 0) в команде ветвления является выражением типа bool, то функция может быть записана следующим образом:

bool prov(int x)

{

  int k = 0, s = 0;

  while (x > 0){

    //сумма цифр числа

    s += x % 10;

    //количество цифр числа

    k++;

    x /= 10;

  }

  return (k % 2 != 0 && s % 5 == 0);

}

7.5. Функции, не возвращающие результат

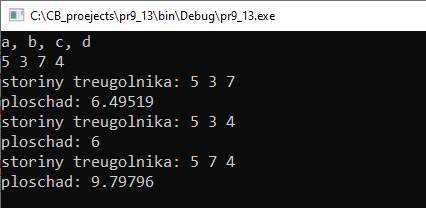
В языке Pascal используются два вида вспомогательных алгоритмов: function и procedure. Функции, которые реализуются в C++, являются аналогом function в Pascal. Аналогом procedure в языке С++ будут функции, тип возвращаемого значения у которых описывается ключевым словом void. Такие функции не возвращают какое-либо значение в качестве результата, поэтому в конце  этих функций отсутствует команда return.

Пример 7.13. Даны отрезки, длины которых равны a, b, c, d соответственно. Для каждой тройки этих отрезков, из которых можно построить треугольник, найти и вывести площадь этого треугольника.

Этапы выполнения задания

I.  Исходные данные: длины отрезков: a, b, c, d.

II. Результат: площади возможных треугольников.

III. Алгоритм решения задачи.

1. Ввод исходных данных. 
2. Для определения, существует ли треугольник с длинами сторон x, y, z, опишем логическую функцию prov. 
3. Треугольник существует, если сумма длин двух сторон больше третьей. 
4. Для каждого из возможных наборов (a, b, c; a, b, d; a, c, d; b, c, d) проверим, существует ли треугольник, и если функция prov вернет true, то вычислим его площадь. 
5. Площадь будем вычислять с помощью функции plos, описанной в примере 7.6. 
6. Для вывода результата опишем функцию vyvod типа void.

IV. Описание переменных: a, b, c, d — int.

Пример 7.13.

V. Программа:

#include <iostream>

#include <cmath>

 

using namespace std;

 

double plos(double x, double y, double z)

{

  double pr = (x + y + z) / 2;

  double pl = sqrt(pr * (pr - x) * (pr - y) * (pr - z));

  return pl;

}

 

bool prov (double x, double y, double z)

{

  return (x < y + z && y < x + z && z < x + y);

}

 

void vyvod (double x, double y, double z)

{

  cout << "storiny treugolnika: ";

  cout << x << " " << y << " " << z;

  cout << endl << "ploschad: ";

  cout << plos(x, y, z) << endl;

}

int main()

{

  double a, b, c, d;

  cout << "a, b, c, d" << endl;

  cin >> a >> b >> c >> d;

  if (prov(a, b, c))

    vyvod(a, b, c);

  if (prov(a, b, d))

    vyvod(a, b, d);

  if (prov(a, c, d))

    vyvod(a, c, d);

  if (prov(b, c, d))

    vyvod(b, c, d);

  return 0;

}

 VI. Тестирование:

7.6. Рекурсия

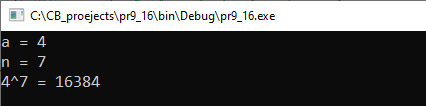
Рекурсия — в программировании вызов подпрограммы (прямо или косвенно) из нее же самой. Количество вложенных вызовов подпрограммы называют глубиной рекурсии.

Различают прямую (простую, непосредственную) и косвенную (сложную, опосредованную) рекурсию.

Прямая рекурсия: при описании функции используется обращение к ней же самой, но с другим набором параметров.

Косвенная рекурсия: подпрограмма вызывает какую-либо другую подпрограмму, в описании которой содержится вызов исходной (например, функция A вызывает функцию B, а функция B вызывает функцию A). Косвенный вызов может быть организован и более сложным образом, т. е. в рекурсию могут быть вовлечены несколько подпрограмм.

Рекурсивная программа позволяет описать повторяющиеся действия без явных повторений частей программы и использования циклов.

Структура рекурсивной функции содержит команду ветвления. Условие в этой команде определяет, когда рекурсия должна прекратиться. По одной из веток этой команды должен происходить хотя бы один рекурсивный вызов (прямой или косвенный) функцией самой себя. Правильно написанная рекурсивная функция должна гарантировать, что через конечное число рекурсивных вызовов будет достигнуто выполнение условия прекращения рекурсии, в результате чего цепочка последовательных рекурсивных вызовов прервется и выполнится возврат.

Любая рекурсивная функция может быть реализована не рекурсивно.

Пример 7.14. Описать алгоритм Евклида с помощью рекурсивной функции.

Этапы выполнения задания

I. Исходные данные: два числа a, b.

II. Результат: НОД (a, b).

III. Алгоритм решения задачи.

1. Ввод исходных данных. 
2. Условием прекращения рекурсии будет равенство чисел. Если числа не равны, то вызываем саму функцию gcd. При этом один из параметров заменяем на разность. 
3. Вывод результата.

IV. Описание переменных: a, b, c, d — int.

Пример 7.15. Написать программу, которая выводит разложение числа на простые множители.

Этапы выполнения задания

I.     Исходные данные: число n.

II.     Результат: простые множители числа a.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Для получения разложения число нужно поочередно пытаться делить на простые числа: 2, 3, 5... . Если разделилось, то данное число входит в разложение и нужно попытаться разделить на него полученное частное, если нет, то попытаемся делить на следующее простое. Процесс заканчивается, когда в частном получаем 1.
3. Опишем рекурсивную функцию razlog(a, b).

3.1. Параметр а — число которое пытаемся делить, параметр b — число, на которое пытаемся делить. 
3.2. Условие прекращения рекурсии — параметр a равен 1. 
3.3. Если a делится на b, то при вызове функции первый параметр заменяем частным a / b, если нет, то второй параметр увеличиваем на 1. 
3.4. При такой организации вычислений можно не проверять, что текущий делитель является простым числом, поскольку ни на одно составное текущее значение первого параметра разделиться не сможет. 
3.5. Вывод результата будет осуществляться при возврате из рекурсии.

IV. Описание переменных: n — int. 

С помощью рекурсии удобно реализовывать решение таких задач, в которых сам реализуемый алгоритм по сути рекурсивен. Достаточно просто описать рекурсивную функцию, когда решение задачи может быть описано с помощью рекуррентного соотношения.

Пример 7.16. По определению . То есть для того, чтобы найти значение an необходимо выполнить  n – 1 умножений. Алгоритм быстрого (бинарного) возведения в степень позволяет сократить количество умножений. Алгоритм (для  n ≥ 0) может быть описан с помощью следующего рекуррентного соотношения:

a to the power of n space equals space open curly brackets table attributes columnalign left end attributes row cell 1 comma space a space equals space 0 end cell row cell open parentheses a to the power of n over 2 end exponent close parentheses squared comma space space space a space space long dash space четное end cell row cell a space space asterisk times space a to the power of n space – space 1 end exponent comma space space n space long dash space нечетное end cell end table close

Написать программу, которая находит an, используя описанный выше алгоритм.

Этапы выполнения задания

I. Исходные данные: числа a и n.

II. Результат: значение an.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Опишем рекурсивную функцию binpow(x, k).

2.1. Параметр x — основание степени, параметр k — показатель.
2.2. Условие прекращения рекурсии — параметр k равен 0. Функция должна вернуть 1. 
2.3. Если k — четное, то при вызове функции второй параметр уменьшаем в 2 раза, если нечетное, то второй параметр уменьшаем на 1.

3. Вывод результата.

IV. Описание переменных: a, n — int.

В некоторых декларативных или чисто функциональных языках (таких как Пролог или Haskell) нет синтаксических средств для организации циклов. В них рекурсия является единственным доступным механизмом для организации повторяющихся вычислений.

Вопрос о желательности использования рекурсивных функций в программировании неоднозначен: с одной стороны, рекурсивная форма может быть структурно проще и нагляднее, в особенности когда сам реализуемый алгоритм по сути рекурсивен. С другой стороны, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.

Рекурсия лежит в основе построения фрактальных изображений.

Пример 7.14.

V. Программа:

#include <iostream>

 

using namespace std;

 

int gcd (int x, int y)

{

  if (x == y)

    return x;

  else

    if (x > y)

      gcd(x - y, y);

    else

      gcd(x, y - x);

}

int main()

{

  int a, b;

  cout << "vvedi 2 chisla" << endl;

  cin >> a >> b;

  int d = gcd(a, b);

  cout << "NOD = " << d << endl;

  return 0;

}

 VI.  Тестирование:

Рекурсивная функция для вычисления НОД двух чисел может быть записана с использованием тернарной (от лат. ternarius — тройной) условной операции.

int gcd (int a, int b)

{

  return b ? gcd (b, a % b) : a;

}

Операция, структурно записываемая как o1 : o2 : o3, возвращает свой второй (o2) или третий (o3) операнд в зависимости от значения логического выражения, заданного первым операндом (o1).

Пример 7.15.

V. Программа:

#include <iostream>

 

using namespace std;

 

void razlog (int a, int b)

{

  if (a > 1)

    if ( a % b == 0){

      razlog(a / b, b);

      cout << b << " ";

    }

    else

      razlog(a, b + 1);

}

int main()

{

  int n;

  cout << "n = ";

  cin >> n;

  razlog(n, 2);

  return 0;

}

 

VI. Тестирование:

VII. Анализ результата.

Чтобы понять, почему мы перебираем простые множители, начиная с меньшего, а программа выводит их в обратном порядке, распишем порядок выполнения команд в программе.

№

a

b

Комментарии

1

60

2

a > 1, 60 % 2 = 0, вызов (60 / 2, 2), после вызова есть команда вывода

2

30

2

a > 1, 30 % 2 = 0, вызов (30 / 2, 2), после вызова есть команда вывода

3

15

2

a > 1, 15 % 2 ≠ 0, вызов (15, 3) после вызова нет команд

4

15

3

a > 1, 15 % 3 = 0, вызов (15 / 3, 3), после вызова есть команда вывода

5

5

3

a > 1, 5 % 3 ≠ 0, вызов (5, 4), после вызова нет команд

6

5

4

a > 1, 5 % 4 ≠ 0, вызов (5, 5), после вызова нет команд

7

5

5

a > 1, 5 % 5 = 0, вызов (5 / 5, 5), после вызова есть команда вывода

8

1

5

условие a > 1 не выполняется; при этом вызове функция закончила работу, однако не завершена работа при тех вызовах, после которых есть вывод.

9

5

5

вывод b = 5

10

15

3

вывод b = 3

11

30

2

вывод b = 2

12

60

2

вывод b = 2

Сохранение вызовов рекурсивной функции вместе со значениями параметров и адресом возврата обеспечивает механизм стека[1] вызовов. Каждый рекурсивный вызов требует некоторого количества оперативной памяти компьютера, поэтому при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов.

Пример 7.16.

V. Программа:

#include <iostream>

 

using namespace std;

 

int binpow(int x, int k)

{

  if (k == 0)

    return 1;

  if (k % 2 == 1)

    return binpow(x, k-1) * x;

  else {

    int b = binpow(x, k / 2);

    return b * b;

  }

}

 

int main()

{

  int a, n;

  cout << "a = ";

  cin >> a;

  cout << "n = ";

  cin >> n;

  cout << a << "^" << n << " = ";

  cout << binpow(a, n) << endl;

  return 0;

}

 VI. Тестирование:


[1] С понятием стека вы познакомитесь позже.

Вопросы к параграфу

1. Что такое вспомогательный алгоритм?

2. Как называют вспомогательный алгоритм, записанный на языке программирования?

3. Какие подпрограммы реализованы в языке С++?

4. Какой формат имеет объявление функции в С++?

5. Где размещается определение функции?

6. Что такое формальные параметры? Что такое фактические параметры?

7. Что понимают под рекурсией?

Упражнения

  

1. Напишите программы для решения задач. Оформите вычисление указанных функций в качестве подпрограмм.

1. Дано вещественное значение x. Получить

begin mathsize 16px style f space left parenthesis 2 x comma space 3 right parenthesis space plus space f space left parenthesis 3 comma 5 space – space x right parenthesis comma space где space f space left parenthesis a comma space b right parenthesis equals fraction numerator 2 a space – b over denominator 5 space – space a end fraction. end style

2. Даны вещественные значения t и s. Получить

f space left parenthesis t comma space – space 2 s comma space 1.17 right parenthesis space plus space f space left parenthesis 2.2 comma space t comma space t space – space s right parenthesis comma space где space f space left parenthesis a comma space b comma space c right parenthesis equals fraction numerator 2 a space – b space plus space square root of c over denominator 5 space plus space open vertical bar с close vertical bar end fraction.

3. Дано действительное число y. Получить

fraction numerator 1.7 f space left parenthesis 0.25 comma space 3 right parenthesis space plus 2 space f space left parenthesis 1 plus y comma space 4 right parenthesis over denominator 6 space – space f left parenthesis y squared space – space 2 comma space 5 right parenthesis end fraction comma space где space f space left parenthesis x comma space k right parenthesis equals fraction numerator x to the power of 2 k space plus space 1 end exponent over denominator left parenthesis 2 k right parenthesis factorial end fraction.

2. Напишите программы для решения задач, используя только функции, описанные в примере 7.5, и арифметические действия (нельзя использовать ветвления, циклы и другие функции).

1. Даны три различных числа. Вывести то, которое не равно минимальному и не равно максимальному из введенных чисел.

Подсказка. От суммы трех чисел отнять минимальное и максимальное.

2. Даны четыре различных числа. Вывести их в порядке возрастания.

Подсказка. Найти min(max(a, b)), max(c, d)  и max(min(a, b)), min(c, d).

3⃰. Даны пять различных чисел. Вывести в порядке убывания те три из них, которые не совпадают с минимальным и максимальным из введенных чисел.

3. Напишите программы для решения геометрических задач.

1. Треугольник задан координатами своих вершин. Найти периметр треугольника. Вычисление длины отрезка оформить в виде подпрограммы.
2. Четырехугольник задан координатами своих вершин. Найти периметр четырехугольника. Вычисление длины отрезка оформить в виде подпрограммы.
3. Выпуклый четырехугольник задан длинами своих сторон и диагональю. Найти площадь четырехугольника как сумму площадей двух треугольников. Вычисление площади треугольника оформить в виде подпрограммы.
4. Выпуклый пятиугольник задан длинами своих сторон и двумя диагоналями, проведенными из одной вершины. Найти площадь пятиугольника как сумму площадей трех треугольников. Вычисление площади треугольника оформить в виде подпрограммы.

4. В примерах 7.9, 7.10, 7.11 и 7.14 приведены различные реализации алгоритма Евклида. Протестируйте эти алгоритмы на различных наборах чисел. Сравните время работы алгоритмов. Время можно посмотреть в консольном окне (программу скомпилируйте в режиме debug).

1. Переберите значения а и b от 2 до 100 000. Найдите НОД(a, b) для всех возможных пар. Значения а и b оба возрастают от 2 до 100 000. 
2. Переберите значения а и b от 2 до 100 000. Найдите НОД(a, b) для всех возможных пар. Значения a возрастают от 2 до 100 000, значения b  убывают от 100 000 до 2. 
3. Значения а и b получают случайным образом. Количество значений  100 000, диапазон [2; 1000]. 
4. Значения а и b получают случайным образом. Количество значений  100 000, диапазон [2; 1 000 000]. 

5. Используя функцию для вычисления НОД(a, b), решите следующие задачи:

1. Напишите программу, которая найдет НОД четырех чисел.
2. Напишите программу, которая найдет НОК (наименьшее общее кратное) двух чисел.
3. Вводятся числитель и знаменатель правильной дроби. Напишите программу, которая сократит дробь.
4. Две правильные дроби заданы своими числителями и знаменателями. Напишите программу, которая найдет их сумму. Ответ выведите в виде смешанной дроби.
5. Заданы два натуральных числа в десятичной системе счисления, состоящие из единиц. В первом числе ровно n единиц, а во втором их ровно m. Вводятся числа n и m. Напишите программу, которая найдет НОД чисел, состоящих из n и m единиц соответственно.
6. Катя решила пригласить к себе в гости n друзей. Так как ее друзья очень любят фрукты, то в качестве угощения для них она купила m одинаковых апельсинов. Она хочет разрезать каждый апельсин на одинаковое число равных долек так, чтобы их можно было распределить между гостями (сама Катя апельсины есть не будет) и всем гостям досталось поровну долек. Напишите программу, которая вычисляет минимальное количество долек, на которое необходимо разрезать каждый апельсин, чтобы были выполнены указанные выше условия. Пример: при n = 2, m = 5 ответ 2.
7. Параллель десятых классов написала контрольную работу. В результате ровно a % учащихся получили «отлично», ровно b % — «хорошо», ровно c % — «удовлетворительно», а остальные d % написали контрольную  неудовлетворительно. Какое минимальное количество учащихся должно быть в параллели десятых классов для того, чтобы могли получиться такие результаты? Вводятся 4 целых числа от 0 до 100:
a, b, c, d (a + b + c + d = 100). Выведите единственное целое положительное число — минимальное возможное количество учащихся в параллели.

6. Даны два натуральных числа n и m (n < m). Написать программу, которая выведет все числа, принадлежащие отрезку [n; m] и удовлетворяющие условиям, описанным ниже. Предусмотреть случай, когда таких чисел нет. Проверку одного числа оформить в виде подпрограммы.

1. Число является «хорошим». (Натуральное число назовем хорошим, если оно делится на сумму своих цифр.) 
2. Цифры числа расположены в порядке возрастания. 
3. Число является палиндромом (перевертышем) четной длины. 
4. Число является «счастливым» — сумма цифр числа, стоящих на первых k местах, равна сумме цифр числа, стоящих на последних k местах. (k — половина количества цифр числа.) 
5. Число является «счастливым» — сумма цифр числа, стоящих на нечетных местах, равна сумме цифр числа, стоящих на четных местах.
6. Число является числом Армстронга. (Натуральное число из k цифр является числом Армстронга, если сумма его цифр, возведенных в k-ю степень, равна самому числу, например 153 = 13 + 53 + 33, k = 3.)
7. Число является треугольным. (Треугольное число — число кружков, которые могут быть расставлены в форме правильного треугольника. Представляется в виде fraction numerator k left parenthesis k space plus space 1 right parenthesis over denominator 2 end fraction,  например число begin mathsize 16px style 15 space equals space fraction numerator 5 space asterisk times space 6 over denominator 2 end fraction end style.)

7. Напишите программы для решения задач, оформив подходящие подпрограммы.

1. Треугольник задан длинами своих сторон. Найти длины его высот. 
2. Даны координаты вершин треугольника и координаты некоторой точки внутри него. Найти расстояние до ближайшей стороны треугольника.

Подсказка. Это расстояние является высотой одного из полученных треугольников.

3. Даны координаты вершин четырехугольника и координаты некоторой точки внутри него. Найти расстояние до ближайшей вершины четырехугольника. 
4. Три прямоугольника со сторонами, параллельными осям координат, заданы координатами своих диагоналей. Выписать все четыре вершины для каждого из прямоугольников и найти их площади.
5. Два прямоугольника со сторонами, параллельными осям координат, заданы координатами своих диагоналей. Проверить, верно ли, что прямоугольник с меньшей площадью целиком находится внутри прямоугольника с большей площадью. Если «да», то найти площадь получившейся «рамки».