§ 3. Превращения энергии при гармонических колебаниях
|
При гармонических колебаниях полная механическая энергия системы остается неизменной, хотя скорость груза и его смещение непрерывно изменяются с течением времени. Какие превращения энергии наблюдаются в системе при этом? Как вычислить кинетическую или потенциальную энергию в любой момент времени? |
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или силовыми полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Привести в движение колебательную систему можно либо посредством отклонения ее из положения равновесия, либо сообщая телу начальную скорость (т. е. посредством толчка). В первом случае мы сообщаем системе дополнительную потенциальную энергию, а во втором — дополнительную кинетическую энергию.
Если силой трения можно пренебречь, то при колебаниях механическая энергия системы сохраняется. При этих условиях для данной системы выполняется закон сохранения механической энергии:
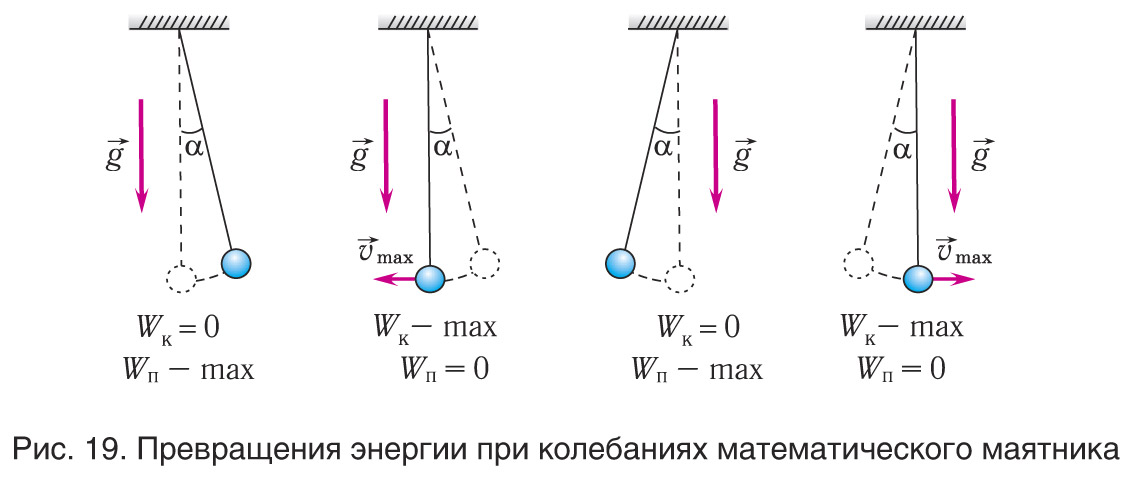
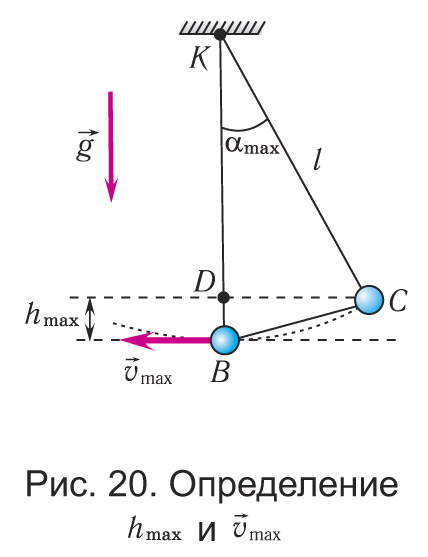
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю. При отклонении маятника на угол (рис. 19, 20), соответствующий его максимальному смещению от положения равновесия (тело в точке С), потенциальная энергия маятника максимальна, а кинетическая энергия равна нулю:
Поскольку в момент прохождения положения равновесия (тело в точке В) потенциальная энергия маятника равна нулю Wп = 0, то из закона сохранения механической энергии следует (см. рис. 20), что , т. е. что кинетическая энергия маятника (а следовательно, и скорость) в этот момент будет максимальна:
Таким образом, в положении равновесия потенциальная энергия маятника полностью переходит в кинетическую, а в положениях максимального отклонения — кинетическая энергия полностью переходит в потенциальную.
Приравнивая полные механические энергии маятника в точках С и В, получим:
| (1) |
Отсюда найдем модуль максимальной скорости маятника:
| (2) |
В любом промежуточном положении
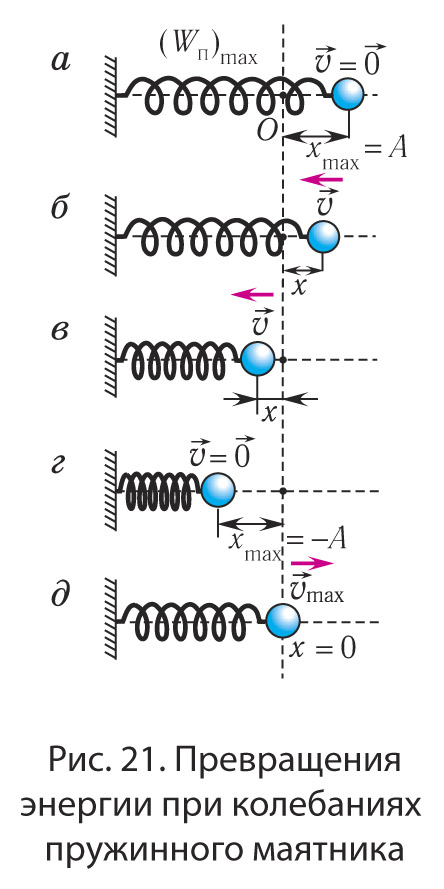
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 21).
В крайних точках, когда и скорость маятника v = 0, кинетическая энергия
груза полностью переходит в потенциальную энергию деформированной пружины (см.рис 21, а, г):
|
|
Таким образом, механическая энергия маятника пропорциональна квадрату амплитуды его колебаний.
В положении равновесия, когда , вся энергия мятника переходит в кинетическую энергию груза (см. рис. 21, д):
|
где υmax — модуль максимальной скорости груза при колебаниях.
В промежуточных точках полная энергия:
|
С учетом выражений кинематического закона движения груза и проекции скорости груза
, а также для
, находим его потенциальную энергию:
и кинетическую энергию:
в произвольный момент времени t .
Тогда полная механическая энергия пружинного маятника в этот же момент времени есть величина постоянная и равная
Таким образом, начальное смещение определяет максимальную потенциальную, а скорость υmax определяет максимальную кинетическую энергию колеблющегося тела.
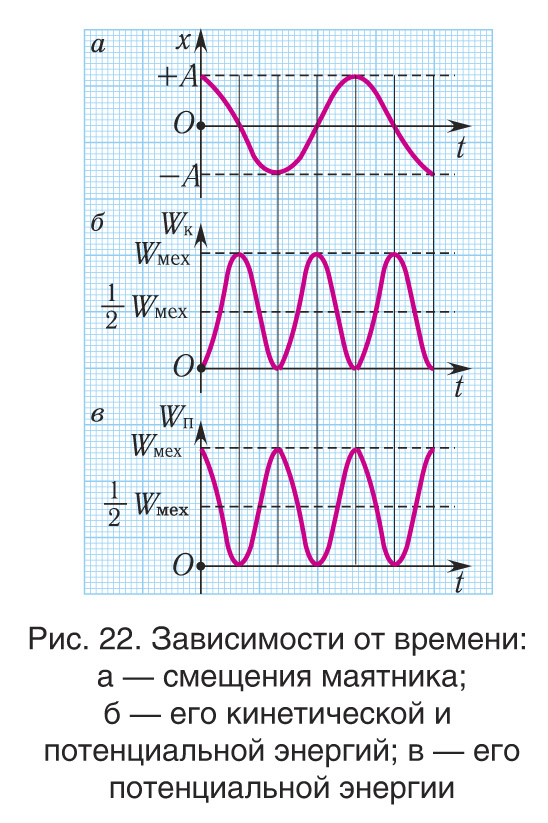
При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом потенциальной энергии в кинетическую и обратно. Такие превращения энергии происходят с вдвое большей частотой (рис. 22, а, б), чем сами колебания. Действительно, дважды за период механическая энергия будет полностью превращаться в потенциальную (в двух крайних положениях) и дважды за период — в кинетическую (при прохождении через положение равновесия) (рис. 22, в).