§ 3. Превращения энергии при гармонических колебаниях
| Сайт: | Профильное обучение |
| Курс: | Физика. 11 класс |
| Книга: | § 3. Превращения энергии при гармонических колебаниях |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 17 Август 2025, 05:21 |
|
При гармонических колебаниях полная механическая энергия системы остается неизменной, хотя скорость груза и его смещение непрерывно изменяются с течением времени. Какие превращения энергии наблюдаются в системе при этом? Как вычислить кинетическую или потенциальную энергию в любой момент времени? |
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или силовыми полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Привести в движение колебательную систему можно либо посредством отклонения ее из положения равновесия, либо сообщая телу начальную скорость (т. е. посредством толчка). В первом случае мы сообщаем системе дополнительную потенциальную энергию, а во втором — дополнительную кинетическую энергию.
Если силой трения можно пренебречь, то при колебаниях механическая энергия системы сохраняется. При этих условиях для данной системы выполняется закон сохранения механической энергии:
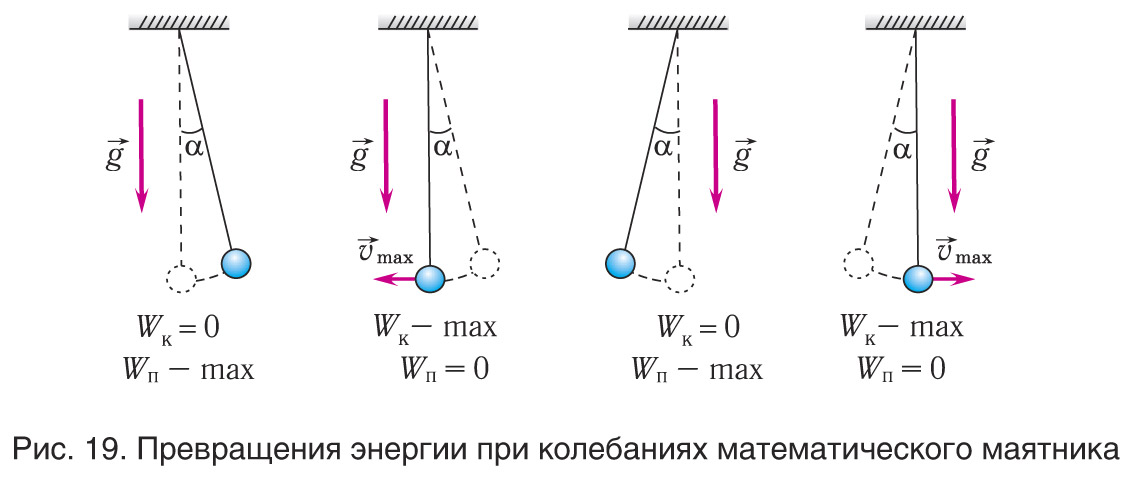
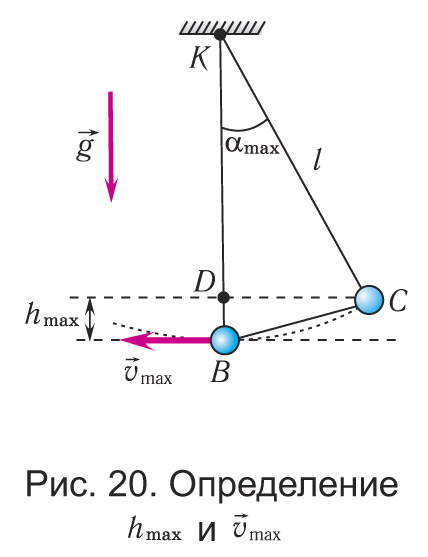
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю. При отклонении маятника на угол (рис. 19, 20), соответствующий его максимальному смещению от положения равновесия (тело в точке С), потенциальная энергия маятника максимальна, а кинетическая энергия равна нулю:
Поскольку в момент прохождения положения равновесия (тело в точке В) потенциальная энергия маятника равна нулю Wп = 0, то из закона сохранения механической энергии следует (см. рис. 20), что , т. е. что кинетическая энергия маятника (а следовательно, и скорость) в этот момент будет максимальна:
Таким образом, в положении равновесия потенциальная энергия маятника полностью переходит в кинетическую, а в положениях максимального отклонения — кинетическая энергия полностью переходит в потенциальную.
Приравнивая полные механические энергии маятника в точках С и В, получим:
| (1) |
Отсюда найдем модуль максимальной скорости маятника:
| (2) |
В любом промежуточном положении
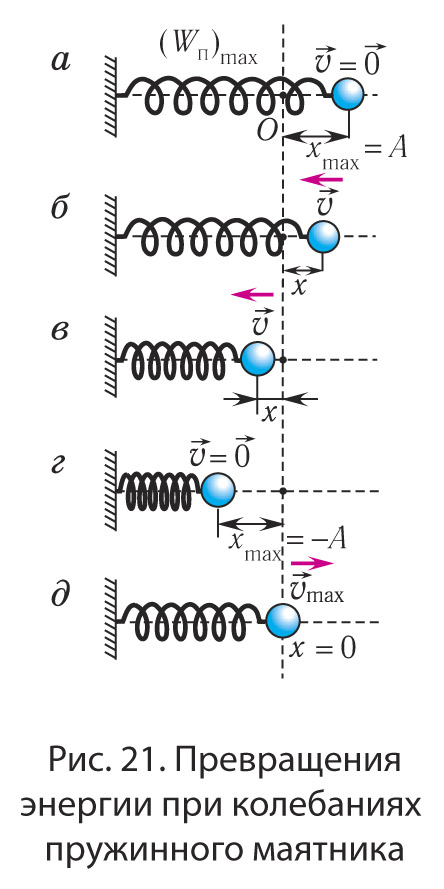
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 21).
В крайних точках, когда и скорость маятника v = 0, кинетическая энергия
груза полностью переходит в потенциальную энергию деформированной пружины (см.рис 21, а, г):
|
|
Таким образом, механическая энергия маятника пропорциональна квадрату амплитуды его колебаний.
В положении равновесия, когда , вся энергия мятника переходит в кинетическую энергию груза (см. рис. 21, д):
|
где υmax — модуль максимальной скорости груза при колебаниях.
В промежуточных точках полная энергия:
|
С учетом выражений кинематического закона движения груза и проекции скорости груза
, а также для
, находим его потенциальную энергию:
и кинетическую энергию:
в произвольный момент времени t .
Тогда полная механическая энергия пружинного маятника в этот же момент времени есть величина постоянная и равная
Таким образом, начальное смещение определяет максимальную потенциальную, а скорость υmax определяет максимальную кинетическую энергию колеблющегося тела.
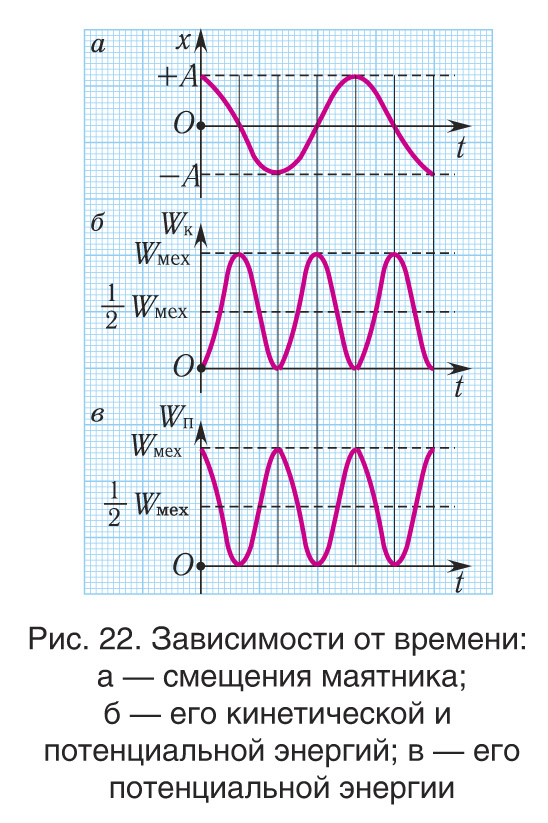
При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом потенциальной энергии в кинетическую и обратно. Такие превращения энергии происходят с вдвое большей частотой (рис. 22, а, б), чем сами колебания. Действительно, дважды за период механическая энергия будет полностью превращаться в потенциальную (в двух крайних положениях) и дважды за период — в кинетическую (при прохождении через положение равновесия) (рис. 22, в).
Вопросы к параграфу
1. Какой энергией обладает математический маятник при прохождении положения равновесия?
2. Какой энергией обладает пружинный маятник при наибольшем смещении от положения равновесия?
3. Чем отличаются потенциальные энергии математического и пружинного маятников?
4. Как изменяется энергия маятника при колебаниях?
5. Запишите формулы для определения механической энергии колеблющегося тела при прохождении им положения равновесия и при максимальном смещении из него.
6. Как связана энергия пружинного (математического) маятника (гармонического осциллятора) с его амплитудой?
Примеры решения задач
1. Определите полную механическую энергию W колебаний груза массой m = 100 г на пружине, если он совершает гармонические колебания с циклической частотой и амплитудой А = 4,0 см.
m = 100 г = 0,10 кг
A = 4,0 см = 0,40 м
Решение
Энергия колебаний груза:
где k — жесткость пружины.
Так как циклическая частота колебаний груза определяется
, то
.
Окончательно,
Ответ: W = 12 мДж.
1-1. Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние и при прохождении положения равновесия достигает скорости, модуль которой
. Определите период T колебаний маятника.
Решение
По закону сохранения механической энергии
Откуда
Ответ:
1-2. Груз массой находится на гладкой горизонтальной поверхности и закреплен к опоре на легкой пружине жесткостью
. Его смещают на расстояние
от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой
. Определите потенциальную
и кинетическую
энергию груза в начальный момент времени. Запишите кинематический закон движения груза
.
Решение
Потенциальная энергия груза определяется выражением:
,
Кинетическая энергия груза определяется выражением:
,
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний
Откуда:
Циклическая частота:
В начальный момент времени координата груза
.
Откуда начальная фаза
,
Тогда закон гармонических колебаний имеет вид (рис. 22-1):
Ответ: ,
,
Упражнение 3
1. В каких точках траектории при колебаниях математического маятника максимальна энергия:
а) кинетическая Wк;
б) потенциальная Wп? Чему она равна?
2. Математический маятник массой m = 100 г при прохождении положения равновесия имеет скорость, модуль которой . Определите:
а) полную энергию Wмех маятника;
б) максимальную высоту hmax, на которую поднимается маятник.
3. Математический маятник массой m = 100 г выводят из положения равновесия, поднимая его на высоту h = 10 см над начальным уровнем. Определите:
а) изменение потенциальной энергии маятника ΔWп при его отклонении от положения равновесия;
б) его максимальную кинетическую энергию (Wк)max.
4. Тело совершает гармонические колебания. Определите отношение кинетической энергии к ее потенциальной энергии для моментов времени, когда смещение тела от положения равновесия составляет:
а) б)
в) x = A.
5. Груз массой m = 250 г совершает гармонические колебания на пружине жесткостью с амплитудой A = 3,6 см. Определите полную механическую энергию колебаний W, потенциальную Wп и кинетическую Wк энергию в момент времени, когда смещение груза от положения равновесия х = 2,2 см. Потенциальную энергию в положении равновесия считать равной нулю.
6. Груз массой m = 100 г, находящийся на гладкой горизонтальной поверхности, закреплен на пружине жесткостью прикрепленной к опоре. Его смещают из положения равновесия на расстояние х1 = 5,0 см и сообщают ему в направлении от положения равновесия скорость, модуль которой
. Чему равны потенциальная Wп и кинетическая Wк энергия груза в этот момент времени? Запишите кинематический закон его движения.
7. Пружинный маятник, находящийся на гладкой горизонтальной поверхности, вывели из положения равновесия и без толчка отпустили. Через какую часть n периода T кинетическая энергия прикрепленного к пружине тела будет равна потенциальной энергии Wп деформированной пружины?
8. Определите полную механическую энергию Wмех гармонических колебаний материальной точки, если известны ее масса m, частота и амплитуда А колебаний.
9. Заполните приведенную таблицу для колебаний математического маятника, изображенного на рис. 22-2, если шарик массой , высота его подъема от положения равновесия
.
|
Положение маятника |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
10. Определите амплитуду А гармонических колебаний тела, если полная механическая энергия колебаний , а максимальная сила, действующая на тело, —
.
11. Вертикальный пружинный маятник совершает гармонические колебания с амплитудой . Определите смещение
маятника от положения равновесия в точке, в которой на него действует возвращающая сила, модуль которой
, если его полная механическая энергия маятника
.
12. Материальная точка массой совершает гармонические колебания с периодом T и начальной фазой
. Максимальная кинетическая энергия колеблющейся точки равна
. Определите амплитуду A колебаний, модуль максимальной скорости
точки и запишите кинематический закон ее движения
.
13. Пуля массой , движущаяся горизонтально со скоростью, модуль которой
, попала в подвешенный на легкой нити деревянный шар массой
и застряла в нем. При этом нить отклонилась от вертикали на угол
. Определите период T колебаний шара.
14. Телу массой , подвешенному на пружине жесткостью
, в положении равновесия сообщают скорость
, направленную вертикально вниз. Определите путь, пройденный телом за промежуток времени от
до
, считая возникающие колебания гармоническими.
15. Пусть период колебаний математического маятника в шахте глубиной равен T . Определите, на какую высоту H над поверхностью Земли необходимо поднять этот маятник, чтобы период его колебаний не изменился.