Информатика. 10 класс (Повышенный уровень)

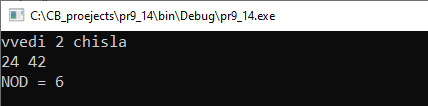
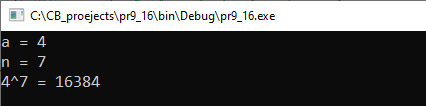
Различают прямую (простую, непосредственную) и косвенную (сложную, опосредованную) рекурсию.

Прямая рекурсия: при описании функции используется обращение к ней же самой, но с другим набором параметров.

Косвенная рекурсия: подпрограмма вызывает какую-либо другую подпрограмму, в описании которой содержится вызов исходной (например, функция A вызывает функцию B, а функция B вызывает функцию A). Косвенный вызов может быть организован и более сложным образом, т. е. в рекурсию могут быть вовлечены несколько подпрограмм.

Рекурсивная программа позволяет описать повторяющиеся действия без явных повторений частей программы и использования циклов.

Структура рекурсивной функции содержит команду ветвления. Условие в этой команде определяет, когда рекурсия должна прекратиться. По одной из веток этой команды должен происходить хотя бы один рекурсивный вызов (прямой или косвенный) функцией самой себя. Правильно написанная рекурсивная функция должна гарантировать, что через конечное число рекурсивных вызовов будет достигнуто выполнение условия прекращения рекурсии, в результате чего цепочка последовательных рекурсивных вызовов прервется и выполнится возврат.

Любая рекурсивная функция может быть реализована не рекурсивно.

Пример 7.14. Описать алгоритм Евклида с помощью рекурсивной функции.

Этапы выполнения задания

I. Исходные данные: два числа a, b.

II. Результат: НОД (a, b).

III. Алгоритм решения задачи.

1. Ввод исходных данных. 
2. Условием прекращения рекурсии будет равенство чисел. Если числа не равны, то вызываем саму функцию gcd. При этом один из параметров заменяем на разность. 
3. Вывод результата.

IV. Описание переменных: a, b, c, d — int.

Пример 7.15. Написать программу, которая выводит разложение числа на простые множители.

Этапы выполнения задания

I.     Исходные данные: число n.

II.     Результат: простые множители числа a.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Для получения разложения число нужно поочередно пытаться делить на простые числа: 2, 3, 5... . Если разделилось, то данное число входит в разложение и нужно попытаться разделить на него полученное частное, если нет, то попытаемся делить на следующее простое. Процесс заканчивается, когда в частном получаем 1.
3. Опишем рекурсивную функцию razlog(a, b).

3.1. Параметр а — число которое пытаемся делить, параметр b — число, на которое пытаемся делить. 
3.2. Условие прекращения рекурсии — параметр a равен 1. 
3.3. Если a делится на b, то при вызове функции первый параметр заменяем частным a / b, если нет, то второй параметр увеличиваем на 1. 
3.4. При такой организации вычислений можно не проверять, что текущий делитель является простым числом, поскольку ни на одно составное текущее значение первого параметра разделиться не сможет. 
3.5. Вывод результата будет осуществляться при возврате из рекурсии.

IV. Описание переменных: n — int. 

С помощью рекурсии удобно реализовывать решение таких задач, в которых сам реализуемый алгоритм по сути рекурсивен. Достаточно просто описать рекурсивную функцию, когда решение задачи может быть описано с помощью рекуррентного соотношения.

Пример 7.16. По определению . То есть для того, чтобы найти значение aⁿ необходимо выполнить  n – 1 умножений. Алгоритм быстрого (бинарного) возведения в степень позволяет сократить количество умножений. Алгоритм (для  n ≥ 0) может быть описан с помощью следующего рекуррентного соотношения:

Написать программу, которая находит aⁿ, используя описанный выше алгоритм.

Этапы выполнения задания

I. Исходные данные: числа a и n.

II. Результат: значение aⁿ.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Опишем рекурсивную функцию binpow(x, k).

2.1. Параметр x — основание степени, параметр k — показатель.
2.2. Условие прекращения рекурсии — параметр k равен 0. Функция должна вернуть 1. 
2.3. Если k — четное, то при вызове функции второй параметр уменьшаем в 2 раза, если нечетное, то второй параметр уменьшаем на 1.

3. Вывод результата.