§ 13. Колькасць цеплаты
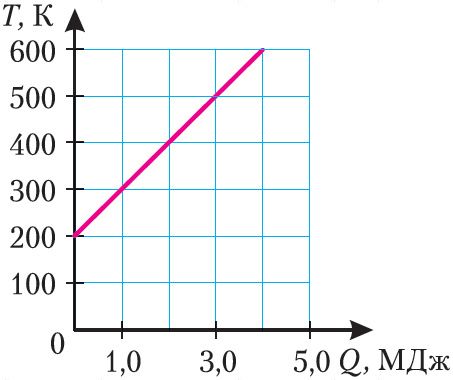
Прыклад 1. На малюнку 77 прыведзены графік залежнасці абсалютнай тэмпературы цела, якое награвалася, ад перададзенай яму колькасці цеплаты. Выкарыстоўваючы табліцу, вызначце рэчыва, з якога выраблена цела, калі яго маса m = 40 кг.
Рашэнне. Для таго каб вызначыць рэчыва, з якога выраблена цела, знойдзем яго ўдзельную цеплаёмістасць с. Аналізуючы графік, робім выснову, што пры награванні цела ад тэмпературы Т1 = 200 К да тэмпературы Т2 = 600 К яму была перададзена колькасць цеплаты Q = 4,0 · 106 Дж, якую можна разлічыць па формуле Q = cm(Т2 – Т1).
Значыць, удзельная цеплаёмістасць рэчыва .
.
Атрыманае значэнне ўдзельнай цеплаёмістасці адпавядае волаву.
Адказ: — волава.
Прыклад 2. У налітую ў пасудзіну ваду, маса якой m1 = 800 г і тэмпература t1 = 60 °С, дадалі некаторую колькасць лёду пры тэмпературы t2 = –10 °С. Вызначце масу лёду, калі пасля дасягнення цеплавой раўнавагі тэмпература вадкасці ў пасудзіне t3 = 40 °С. Цеплаёмістасць пасудзіны і страты цяпла можна не прымаць пад увагу. Удзельная цеплаёмістасць вады , лёду
, удзельная цеплата плаўлення лёду
.
m1 = 800 г = 0,800 кг
t1 = 60 °С
t2 = –10 °С
t3 = 40 °С
Рашэнне. Не прымаючы пад увагу страты энергіі ў навакольнае асяроддзе, улічваем толькі абмен энергіяй паміж целамі, што ўвахо дзяць у склад сістэмы. Разгледзім цеплавыя працэсы, якія адбываліся ў сістэме: 1) на гра ванне лёду ад тэмпературы t2 да тэмпературы плаўлення t0 = 0,0 °С: Q1 = c2m2(t0 – t2); 2) плаўленне лёду: Q2 = λm2; 3) награванне вады, якая з’явілася пры плаўленні лёду, ад тэмпературы t0 да тэмпературы t3: Q3 = c1m2(t3 – t0); 4) ахалоджванне цёплай вады масай m1 ад тэмпературы t1 да тэмпературы t3: Q4 = c1m1(t3 – t1). Складзём ураўненне цеплавога балансу: Q1 + Q2 + Q3 + Q4 = 0, або
Адкуль маса лёду:
Адказ: m2 = 0,13 кг.