§ 4. Цеплавая раўнавага. Тэмпература — мера сярэдняй кінетычнай энергіі цеплавога руху часціц рэчыва
![]()
Тэмпература і сярэдняя кінетычная энергія паступальнага руху малекул газу. Значэнне тэмпературы пры вымярэнні ступені нагрэтасці цела вызначаюць па тэмпературным змяненні зручнай для вымярэнняў фізічнай уласцівасці рэчыва. Прыклады тэрмаметрычных уласцівасцей: ціск газу, электрычнае супраціўленне правадніка ці паўправадніка, цеплавое расшырэнне вадкасці або цвёрдага цела. Вызначэнне тэмпературы павінна грунтавацца на такой фізічнай велічыні, якая характарызуе стан цел і з’яўляецца аднолькавай для любых цел, што знаходзяцца ў стане цеплавой раўнавагі. Неабходнай уласцівасцю валодае сярэдняя кінетычная энергія цеплавога руху часціц рэчыва. Цеплавы рух часціц рэчыва істотна змяняецца пры змене яго агрэгатнага стану. Максімальна просты ён у аднаатамнага газу, атамы якога выконваюць толькі паступальны рух.
Возьмем некалькі пасудзін рознай ёмістасці, аснашчаных манометрамі для вымярэння ціску (мал. 16). Запоўніўшы іх рознымі газамі, напрыклад аргонам, неонам і геліем, змесцім спачатку ў пасудзіну з лёдам, які растае (t0 = 0 °С), а затым будзем змяняць тэмпературу змесціва пасудзіны, пакуль яна не стане роўнай тэмпературы кіпення вады (t = 100 °С).
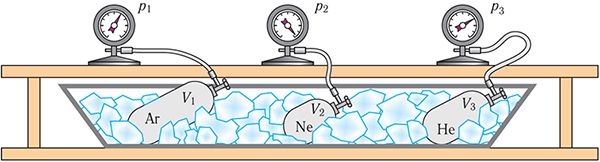
Значэнні ціску газаў у ёмістасцях могуць адрознівацца. Масы газаў можна вызначыць шляхам узважвання адпампаваных і запоўненых ёмістасцей. Ведаючы масу m газу і яго малярную масу М, па формуле можна вылічыць колькасць часціц і, значыць, вызначыць іх канцэнтрацыю
кожнай з ёмістасцей.
Доследным шляхам было ўстаноўлена, што ў стане цеплавой раўнавагі, нягледзячы на розныя значэнні ціску р і канцэнтрацыі n часціц, адносіны ціску да канцэнтрацыі ва ўсіх ёмістасцях аказаліся практычна аднолькавымі:
. Гэтыя адносіны для разрэджаных газаў (задавальняюць патрабаванням мадэлі «ідэальны газ») залежыць толькі ад ступені нагрэтасці цела і характарызуюць тэмпературу газаў у энергетычных адзінках (у СІ вымяраюць у джоўлях). Адзінка вымярэння тэмпературы джоўль нязручная. Напрыклад, тэмпература кіпення вады, выражаная ў джоўлях:
Першапачатковая тэрмаметрыя заснавана на шкале ідэальнага газу, якая ўстанаўліваецца з дапамогай газавага тэрмометра, для якога залежнасць ціску ад тэмпературы прымаюць лінейнай:
(4.1)
дзе k — каэфіцыент прапарцыянальнасці.
Калі пры нулі тэрмаметрычнай шкалы тэрмаметрычная велічыня (ціск газу) становіцца нулём, то такую шкалу называюць абсалютнай шкалой, а тэмпературу, якая адлічваецца па такой шкале, — абсалютнай тэмпературай: p = nkТ. Тэмпература, роўная нулю на такой шкале, — тэмпература, пры якой ціск ідэальнага газу быў бы роўны нулю. Але гэта не азначае, што ідэальны газ можна настолькі ахаладзіць, што яго ціск стане роўны нулю.

Шкалу, якая зусім не залежыць ад фізічных уласцівасцей якіх бы там ні было рэчываў, і таму яе можна лічыць абсалютнай і ўніверсальнай, прапанаваў у 1848 г. вядомы англійскі фізік Уільям Томсан (1824–1907), атрымаўшы за працы ў галіне фізікі у 1892 г. тытул лорда Кельвіна. Таму гэтую шкалу звычайна называюць шкалой Кельвіна.
Шкала Кельвіна зусім не залежыць ад якіх бы там ні было фізічных уласцівасцей рэчываў, таму яе можна лічыць абсалютнай і ўніверсальнай.
Нулявы пункт па шкале Кельвіна адпавядае самай нізкай тэарэтычна магчымай тэмпературы (абсалютны нуль тэмпературы). Тэмпература расталага лёду па гэтай шкале T0 = 273,15 К. Сувязь паміж тэмпературамі па шкале Цэльсія (t) і па шкале Кельвіна (T) мае выгляд: T = t + 273,15.
Адзінка тэмпературы па абсалютнай шкале адзін кельвін (1 К) з’яўляецца асноўнай адзінкай тэмпературы ў СІ і супадае з адным градусам (1 °С) па шкале Цэльсія. Таму рознасць тэмператур па шкале Кельвіна і па шкале Цэльсія аднолькавая, гэта значыць ΔT = Δt (мал. 17).
Выразіце па шкале Кельвіна тэмпературу цела здаровага чалавека.
З асноўнага ўраўнення малекулярна-кінетычнай тэорыі ідэальнага газу (3.2) вынікае: . Значыць, улічваючы выраз (4.1), можна запісаць:
або
(4.2)
Суадносіны (4.2) устанаўліваюць сувязь паміж абсалютнай тэмпературай Т ідэальнага газу і сярэдняй кінетычнай энергіяй паступальнага руху яго часціц. Такім чынам, з формулы (4.2) вынікае, што сярэдняя кінетычная энергія паступальнага руху часціц ідэальнага газу прапарцыянальная яго абсалютнай тэмпературы.
Сярэдняя кінетычная энергія паступальнага руху малекул газаў, якія знаходзяцца ў стане цеплавой раўнавагі, аднолькавая для розных газаў і не залежыць ад масы малекулы газу.
Гэтая выснова, якая грунтуецца на эксперыментах з разрэджанымі газамі, праўдзівая для вадкасцей і цвёрдых цел.
Ураўненне (4.2) можна запісаць наступным чынам: , адкуль
З улікам формулы (4.1) асноўнае ўраўненне малекулярна-кінетычнай тэорыі ідэальнага газу набывае наступны выгляд:
(4.3)
З ураўнення (4.3) відаць, што пры аднолькавых значэннях абсалютнай тэмпературы Т і канцэнтрацыі n часціц ціск любых газаў аднолькавы, незалежна ад таго, з якіх часціц яны складаюцца.
1. У састаў паветра каля зямной паверхні ў невялікай колькасці ўваходзяць інертныя газы: неон (МNe = 20 · 10–3 ) і гелій (МНe = 4,0 · 10–3
). Якая сярэдняя кінетычная энергія цеплавога руху часціц гэтых газаў пры нармальных умовах: p0 = 1,0 · 105 Па, t0 = 0,0 °С? Якія даныя з умовы можна выключыць?
2. Ці супадаюць сярэднія квадратычныя скорасці малекул кіслароду і азоту ў паветры?
1. Якая велічыня характарызуе стан цеплавой раўнавагі?
2. Ці можна звычайным вадкасным тэрмометрам вымераць тэмпературу кроплі вады?
3. Як залежыць сярэдняя кінетычная энергія паступальнага руху малекул ідэальнага газу ад тэмпературы?
4. Пры награванні газу ў балоне сярэдняя квадратычная скорасць малекул павялічылася ў два разы. Як змяніўся ціск газу?
5. Што ўяўляе з сябе абсалютная шкала тэмператур? Што прынята за адзінку абсалютнай тэмпературы ў Сі? Як суадносяцца тэмпературы па шкале Цэльсія і шкале Кельвіна?
6. Як звязаны ціск ідэальнага газу з яго абсалютнай тэмпературай і канцэнтрацыяй малекул?
* Адзінка вымярэння тэмпературы джоўль нязручная. Напрыклад, тэмпература кіпення вады, выражаная ў джоўлях: . ↑