§ 26. Закон Ома для полной электрической цепи. КПД источника тока

Примеры решения задач

Пример 1. Резистор с сопротивлением R = 3,0 Ом подключён к источнику тока с ЭДС calligraphic E = 8,0 В и внутренним сопротивлением r = 1,0 Ом. Определите полезную мощность тока и КПД источника тока в данной цепи.

Дано:
R = 3,0 Ом
calligraphic E = 8,0 В
r = 1,0 Ом
Pполезн — ?
η — ?

Решение: Полезной является мощность тока на внешнем участке цепи, т. е. на резисторе: Pполезн = I2R. С учётом закона Ома для полной цепи I equals fraction numerator calligraphic E over denominator R plus r end fraction получим:

P subscript полезн equals calligraphic E squared R over left parenthesis R plus r right parenthesis squared.

P subscript полезн equals fraction numerator 64 space straight В squared times 3 comma 0 space Ом over denominator left parenthesis 3 comma 0 space Ом plus 1 comma 0 space Ом right parenthesis squared end fraction equals 12 space Вт.

КПД источника тока в данной цепи определим по формуле

straight eta equals fraction numerator R over denominator R plus r end fraction times 100 space percent sign.

straight eta equals fraction numerator 3 comma 0 space Ом over denominator 3 comma 0 space Ом plus 1 comma 0 space Ом end fraction times 100 space percent sign equals 75 space percent sign.

Ответ: Pполезн = 12 Вт, η = 75 %.

Материал повышенного уровня

Пример 2. Конденсатор подключён к источнику тока (рис. 132.1, а). При подключении параллельно конденсатору резистора с сопротивлением R = 20 Ом (рис. 132.1, б) заряд на конденсаторе уменьшился в α = 1,4 раза. Определите внутреннее сопротивление источника тока.

Рис.
Рис. 132.1
Дано:
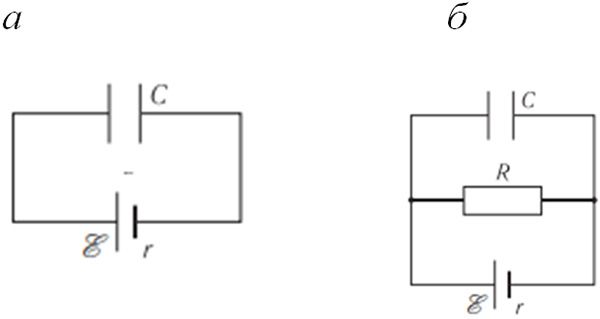
R = 20 Ом
α = q subscript 1 over q subscript 2 = 1,4
R — ?

Решение: При подключении конденсатора к источнику тока напряжение на конденсаторе равно напряжению на полюсах источника (цепь разомкнута, см. рис. 132.1, а) U subscript 1 equals calligraphic E. После того, как параллельно конденсатору подключили резистор (см. рис. 132.1, б), в цепи возник электрический ток. Силу тока можно определить, используя закон Ома для полной цепи: I equals fraction numerator calligraphic E over denominator R plus r end fraction. В этом случае напряжение на конденсаторе стало равно напряжению на резисторе: U subscript 2 equals fraction numerator calligraphic E R over denominator R plus r end fraction. Поскольку напряжение на конденсаторе прямо пропорционально его заряду U subscript 1 equals q subscript 1 over C и U subscript 2 equals q subscript 2 over C, то q subscript 1 over q subscript 2 equals fraction numerator U subscript 1 C over denominator U subscript 2 C end fraction equals fraction numerator calligraphic E open parentheses R plus r close parentheses over denominator calligraphic E R end fraction equals 1 plus r over R equals 1 comma 4 и r = 0,40 R. Таким образом,

r = 0,40 · 20 Ом = 8,0 Ом.

Ответ: r = 8,0 Ом.

Пример 3. Электродвигатель в сети постоянного тока с напряжением U = 120 В потребляет ток силой I = 6,0 А. Определите сопротивление его обмотки, если КПД электродвигателя η = 80 %.

Дано:
U = 120 В
I = 6,0 А
η = 80 %
R — ?

Решение: Мощность, потребляемую электродвигателем, определим по формуле Pполн = IU (1). Часть этой мощности затрачивается на нагревание обмотки: P = I2R, а часть — превращается в полезную механическую мощность Pполезн электродвигателя. На основании закона сохранения энергии

Pполн = I2R + Pполезн.

(2)

Используя формулы (1) и (2), запишем выражение для нахождения полезной мощности электродвигателя:

Pполезн = Pполн - I2R = IU - I2R.

(3)

КПД электродвигателя определим по формуле straight eta equals P subscript полезн over P subscript полн times 100 percent sign.

С учётом формул (1) и (3) получим:

straight eta equals fraction numerator I U minus I squared R over denominator I U end fraction equals 1 minus fraction numerator I R over denominator U end fraction.

(4)

Сопротивление обмотки электродвигателя выразим из формулы (4):

R equals fraction numerator U open parentheses 1 minus straight eta close parentheses over denominator I end fraction.

R equals fraction numerator 120 space straight В space open parentheses 1 minus 0 comma 80 close parentheses over denominator 6 comma 0 space straight А end fraction equals 4 comma 0 space Ом.

Ответ: R = 4,0 Ом.