§ 26. Закон Ома для полной электрической цепи. КПД источника тока
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 26. Закон Ома для полной электрической цепи. КПД источника тока |
| Напечатано:: | Гость |
| Дата: | Monday, 13 October 2025, 18:27 |
В 1826 г. немецкий физик Георг Симон Ом (1787–1854) опытным путём установил, что при постоянной температуре отношение напряжения между концами металлического проводника к силе тока в нём является величиной постоянной. На основании этого был сформулирован закон, названный законом Ома для участка электрической цепи: , где R — сопротивление участка цепи. От чего и как зависит сила тока в замкнутой цепи, содержащей источник тока, т. е. в полной электрической цепи?
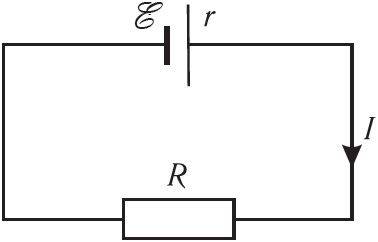
Закон Ома для полной электрической цепи. Рассмотрим электрическую цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. Известны ЭДС источника тока и его сопротивление r, которое называют внутренним. Схема цепи представлена на рисунке 132. Пусть сила тока в цепи I, а напряжение между концами проводника U.
Закон Ома для полной цепи связывает силу тока I в цепи, ЭДС источника тока и полное сопротивление цепи R + r, которое складывается из сопротивлений внешнего (резистор) и внутреннего (источник тока) участков цепи (сопротивлением соединительных проводов пренебрегаем). Эту связь можно установить теоретически на основании закона сохранения энергии.
Если через поперечное сечение проводника за промежуток времени t проходит заряд q, то работу сторонней силы по перемещению электрического заряда можно определить по формуле
Поскольку сила тока , то
(26.1)
В неподвижных проводниках неизменного химического состава в результате работы сторонних сил происходит увеличение только внутренней энергии внешнего и внутреннего участков цепи. Таким образом, при прохождении электрического тока в резисторе и источнике тока выделяется количество теплоты Q, которое можно определить по закону Джоуля–Ленца:
Q = I2Rt + I2rt.
(26.2)
На основании закона сохранения энергии:
Аст = Q.
(26.3)
Подставим формулы (26.1) и (26.2) в равенство (26.3) и в результате математических преобразований получим:
= IR + Ir.
(26.4)
Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Поэтому IR = U — падение напряжения (напряжение) на внешнем участке цепи, Ir — падение напряжения на внутреннем участке цепи.
Выражая силу тока из формулы (26.4), получим:
(26.5)
Формула (26.5) является математическим выражением закона Ома для полной электрической цепи, согласно которому сила тока в полной электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.
Аккумулятор, внутреннее сопротивление которого r = 0,80 Ом, подсоединён к резистору. Чему равна ЭДС аккумулятора, если напряжение на его полюсах U = 6,0 В, а сила тока в цепи I = 0,50 А?
Различные режимы работы электрической цепи. Преобразуем формулу (26.4):
IR = – Ir,
так как IR = U, то
U = − Ir.
(26.6)
Из выражения (26.6) следует, что при разомкнутой цепи (I = 0) напряжение между полюсами источника тока равно его ЭДС: U = . Следовательно, измерить ЭДС источника тока можно, подключив к его полюсам вольтметр с бесконечно большим собственным сопротивлением (чтобы не нарушать режим разомкнутой цепи).
В случае, если сопротивление внешнего участка цепи стремится к нулю (R 0), сила тока возрастает и достигает максимального значения. Падение напряжения на источнике тока при этом равно ЭДС, а напряжение между его полюсами — нулю.
Такой режим работы источника тока называют коротким замыканием, а максимально возможную для данного источника силу тока называют силой тока короткого замыкания:
где r — внутреннее сопротивление источника тока.
Для источников тока с незначительным внутренним сопротивлением (например, у автомобильных аккумуляторов r ≈ 0,01 Ом) режим короткого замыкания чрезвычайно опасен, поскольку может привести к повреждению источника тока и даже быть причиной пожара.
Сила тока при коротком замыкании батарейки Iк.з = 2 А. Когда к батарейке подключили резистор с сопротивлением R = 3 Ом, сила тока стала I = 1 А. Как изменилось полное сопротивление цепи? Чему равно внутреннее сопротивление батарейки?
Коэффициент полезного действия источника тока. При перемещении заряда q на внешнем участке цепи, напряжение на котором U, за промежуток времени t сила электрического поля совершает работу:
A = Uq.
Используя выражение , получим формулу для расчёта работы электрического тока, совершённой на внешнем участке
A = IUt.
![]()
В общем случае работа тока может превращаться в механическую работу Амех электродвигателей, расходоваться на увеличение внутренней энергии участка цепи (выделение количества теплоты Q), обеспечивать увеличение химической энергии ΔEхим , а также преобразовываться в энергию возникающего электромагнитного излучения Eизл:
IUt = Aмех + Q + ΔEхим + Eизл.
Если к источнику тока подключён только электродвигатель, то IUt = Aмех + Q и полезной работой будет Амех.
Если прохождение тока сопровождается химическими реакциями (например, зарядка аккумулятора), то IUt = ΔEхим + Q и полезная работа будет равна ΔEхим.
При работе электроосветительного оборудования IUt = Eизл + Q и полезная работа равна Eизл.
При включении в цепь только электронагревательных приборов IUt = Q и полезная работа равна Q.
При изучении физики в 8-м классе вы узнали, что, согласно экспериментально установленному закону Джоуля‒Ленца, количество теплоты, которое выделяется в проводнике при прохождении электрического тока, определяют по формуле Q = I2Rt.
Следовательно, работа тока на произвольном участке цепи в общем случае не равна количеству теплоты, выделяющемуся на этом участке при прохождении тока, т. е. IUt ≠ I2Rt.
Равенство IUt = I2Rt выполняется только в том случае, если на участке цепи имеет место превращение энергии электрического поля, поддерживаемого источником тока, во внутреннюю энергию этого участка.
Если внешним участком цепи является нагревательный элемент (или резистор), то с учётом закона Джоуля–Ленца формула для расчёта полезной работы электрического тока на внешнем участке цепи:
Aполезн = I2Rt.
Учитывая, что мощность , получим выражение для определения полезной мощности тока на тепловом потребителе, являющемся внешним участком цепи:
Pполезн = I2R = IU.
Поскольку работа сторонних сил источника тока:
Aст = Aполн = It,
то мощность, развиваемая сторонними силами источника тока при наличии в цепи только нагревательного элемента:
Pст = Pполн = I = IU + I2r.
Следовательно, Pполн = Pполезн + I2r.
Коэффициент полезного действия (КПД) источника тока — отношение полезной мощности тока на внешнем участке цепи к полной мощности, развиваемой сторонними силами источника тока:
![]()
Согласно формуле :
Так, например, при зарядке аккумулятора источником тока с ЭДС при силе зарядного тока I КПД этого источника определяют по формуле
.
Если внешний участок цепи — нагревательный элемент, то
Pполезн = I2R,
Pполн = I2(R + r).
Тогда КПД источника тока

1. Сформулируйте закон Ома для полной цепи.
2. Как можно измерить ЭДС источника тока?
3. Какой режим работы электрической цепи соответствует короткому замыканию?
4. Что понимают под силой тока короткого замыкания?
5. Что понимают под полезной работой электрического тока? полной работой источника тока?
6. Как определить полезную мощность электрического тока? полную мощность источника тока?
7. Что называют коэффициентом полезного действия (КПД) источника тока?
Пример 1. Резистор с сопротивлением R = 3,0 Ом подключён к источнику тока с ЭДС = 8,0 В и внутренним сопротивлением r = 1,0 Ом. Определите полезную мощность тока и КПД источника тока в данной цепи.
R = 3,0 Ом
r = 1,0 Ом
η — ?
Решение: Полезной является мощность тока на внешнем участке цепи, т. е. на резисторе: Pполезн = I2R. С учётом закона Ома для полной цепи получим:
КПД источника тока в данной цепи определим по формуле
Ответ: Pполезн = 12 Вт, η = 75 %.
![]()
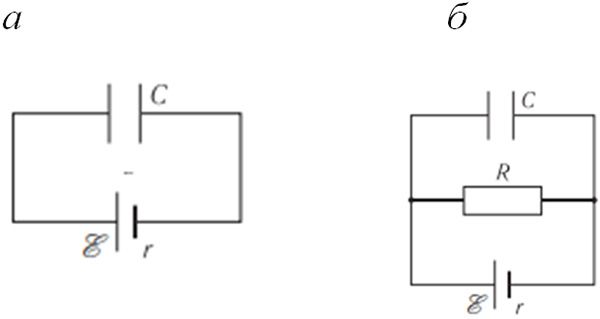
Пример 2. Конденсатор подключён к источнику тока (рис. 132.1, а). При подключении параллельно конденсатору резистора с сопротивлением R = 20 Ом (рис. 132.1, б) заряд на конденсаторе уменьшился в α = 1,4 раза. Определите внутреннее сопротивление источника тока.
R = 20 Ом
α =
Решение: При подключении конденсатора к источнику тока напряжение на конденсаторе равно напряжению на полюсах источника (цепь разомкнута, см. рис. 132.1, а) . После того, как параллельно конденсатору подключили резистор (см. рис. 132.1, б), в цепи возник электрический ток. Силу тока можно определить, используя закон Ома для полной цепи:
. В этом случае напряжение на конденсаторе стало равно напряжению на резисторе:
. Поскольку напряжение на конденсаторе прямо пропорционально его заряду
и
, то
и r = 0,40 R. Таким образом,
r = 0,40 · 20 Ом = 8,0 Ом.
Ответ: r = 8,0 Ом.
Пример 3. Электродвигатель в сети постоянного тока с напряжением U = 120 В потребляет ток силой I = 6,0 А. Определите сопротивление его обмотки, если КПД электродвигателя η = 80 %.
U = 120 В
I = 6,0 А
η = 80 %
Решение: Мощность, потребляемую электродвигателем, определим по формуле Pполн = IU (1). Часть этой мощности затрачивается на нагревание обмотки: P = I2R, а часть — превращается в полезную механическую мощность Pполезн электродвигателя. На основании закона сохранения энергии
Pполн = I2R + Pполезн.
(2)
Используя формулы (1) и (2), запишем выражение для нахождения полезной мощности электродвигателя:
Pполезн = Pполн - I2R = IU - I2R.
(3)
КПД электродвигателя определим по формуле .
С учётом формул (1) и (3) получим:
.
(4)
Сопротивление обмотки электродвигателя выразим из формулы (4):
Ответ: R = 4,0 Ом.
Упражнение 19
1. Резистор с сопротивлением R = 2 Ом подключён к источнику тока с ЭДС = 5 В и внутренним сопротивлением r = 0,5 Ом. Определите силу тока в цепи и падение напряжения на внешнем и внутреннем участках электрической цепи.
2. Реостат подключён к источнику тока с ЭДС = 4 В и внутренним сопротивлением r = 1 Ом. Постройте график зависимости силы тока от сопротивления той части реостата, по которой проходит ток, I = I(R).
3. При подключении к источнику тока с ЭДС = 2,2 В резистора с сопротивлением R = 4,0 Ом сила тока в цепи I = 0,50 А. Определите силу тока при коротком замыкании источника тока.
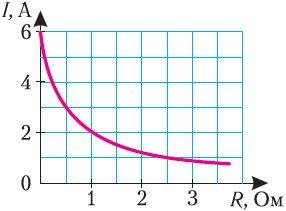
4. На рисунке 133 представлен график зависимости силы тока в реостате от его сопротивления. Определите силу тока при коротком замыкании источника тока и его внутреннее сопротивление.
5. Определите полную мощность, развиваемую источником тока с внутренним сопротивлением r = 0,50 Ом, при подключении к нему резистора с сопротивлением R = 2,0 Ом, если напряжение на резисторе U = 4,0 В.
6. Спираль нагревательного элемента, сопротивление которой R = 38 Ом, подключена к источнику тока с ЭДС = 12 В и внутренним сопротивлением r = 2,0 Ом. Определите количество теплоты, которое выделится в спирали за промежуток времени t = 10 мин.
7. Два параллельно соединённых резистора, сопротивления которых R1 = 4,0 Ом и R2 = 6,0 Ом, подключили к источнику тока с ЭДС = 12 В и внутренним сопротивлением r = 0,60 Ом. Определите напряжение на резисторах и силу тока в каждом из них.
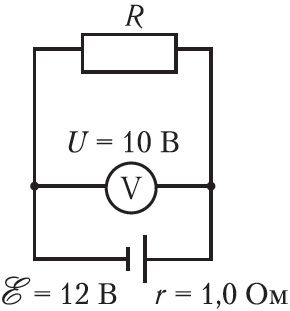
8. На рисунке 134 представлена схема электрической цепи, состоящей из источника тока, резистора и идеального вольтметра. Определите работу электрического тока на внешнем участке цепи за промежуток времени t = 10 мин и КПД источника тока.

9. На рисунке 135 представлена схема электрической цепи, состоящей из источника тока, ключа и трёх резисторов. Выберите из предложенного перечня три верных утверждения. Укажите их номера.
1) Полезную мощность тока на внешнем участке цепи при разомкнутом ключе можно определить по формуле .
2) Мощность, развиваемую сторонними силами источника тока при замкнутом ключе, можно определить по формуле .
3) Полезную работу тока на внешнем участке цепи при замкнутом ключе можно определить по формуле .
4) Работу сторонних сил источника тока при разомкнутом ключе можно определить по формуле .
5) КПД источника тока при разомкнутом ключе η = 80 %.
![]()
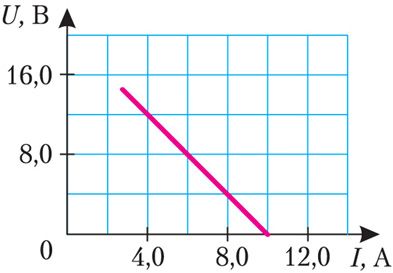
10. Вольт-амперная характеристика, построенная по результатам экспериментального исследования зависимости напряжения на реостате от силы тока в нём, представлена на рисунке 135.1. Определите силу тока при коротком замыкании источника тока и его ЭДС.
11. Для проведения экспериментального исследования была собрана электрическая цепь, состоящая из источника тока, ключа, соединительных проводов, реостата, амперметра и вольтметра. В ходе исследования зависимости напряжения на реостате от силы тока в нём была составлена таблица.
| U, В | 0,50 | 0,70 | 0,80 | 0,90 |
| I, А | 0,70 | 0,50 | 0,40 | 0,30 |
Определите ЭДС источника тока и его внутреннее сопротивление.

12. Модуль напряжённости электростатического поля плоского конденсатора, подключённого к источнику постоянного тока (рис. 135.2), Е = 3,0 . ЭДС источника тока
= 0,16 кВ, а его внутреннее сопротивление r = 5,0 Ом. Определите расстояние между обкладками конденсатора, если сопротивление резистора R = 15 Ом.
13. Электродвигатель в сети постоянного тока с напряжением U = 220 В потребляет ток силой I = 12 А. Сопротивление обмотки электродвигателя R = 5,0 Ом. Определите механическую мощность и КПД электродвигателя.
14. В электрический чайник налили воду и подключили к источнику тока с ЭДС = 140 В и внутренним сопротивлением r = 4,0 Ом. Вольтметр, подключённый к полюсам источника тока, показывает напряжение U = 120 В. Определите, на сколько увеличится температура воды за промежуток времени τ = 2,0 мин, если её объём V = 1,0 л и КПД чайника η = 70 %. Плотность воды ρ = 1,0 · 103
, удельная теплоёмкость воды c = 4,2 · 103
.