§ 17. Взаимодействие точечных зарядов. Закон Кулона
Пример 1. Два точечных заряда находятся в керосине на расстоянии r1 = 42 см. Определите, на каком расстоянии должны находиться эти заряды в глицерине, чтобы модуль сил их электростатического взаимодействия остался прежним. Диэлектрические проницаемости керосина ε1 = 2,0, глицерина ε2 = 56,2.
r1 = 42 см
Fк1 = Fк2
ε1 = 2,0
ε2 = 56,2
Решение: Поскольку Fк1 = Fк2, то, воспользовавшись законом Кулона, можно записать: .
Следовательно, .
Ответ: r2 = 7,9 см.
Пример 2. Точечные заряды q1 = 3,4 нКл и q2 = –5,6 нКл находятся в вакууме на расстоянии r = 36 см. Определите модуль и направление результирующей силы, действующей на заряд q3 = 3,2 нКл, помещённый в точку пространства, находящуюся на середине отрезка, соединяющего эти заряды.
q1 = 3,4 нКл = 3,4 · 10–9 Кл
q2 = –5,6 нКл = –5,6 · 10–9 Кл
r = 36 см = 0,36 м
q3 = 3,2 нКл = 3,2 · 10–9 Кл
Решение: Изобразим на рисунке силы и
, действующие на точечный заряд q3 со стороны точечных зарядов q1 и q2 соответственно. Построив векторную сумму сил
и
, определим, что результирующая
этих сил направлена к заряду q2 (рис. 102).
Поскольку силы и
направлены одинаково, то модуль результирующей силы
.
Таким образом,
Ответ: Fp = 8,0 мкН; сила направлена к заряду q2.
![]()
Пример 3. Две бусинки, электрические заряды которых q1 = 40 нКл и q2 = 90 нКл, закреплены на непроводящем стержне на расстоянии r = 40 см друг от друга. Определите: а) где надо поместить третью бусинку, имеющую заряд q3, чтобы она оказалась в равновесии; б) каким должен быть заряд q3 третьей бусинки, чтобы результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равнялась нулю.
q1 = 40 нКл = 4,0·10–8 Кл
q2 = 90 нКл = 9,0·10-8 Кл
r = 40 см = 0,40 м
q3 — ?
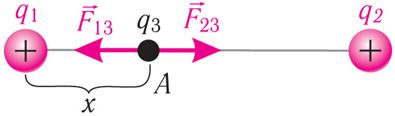
Решение: а) Третья бусинка, имеющая заряд q3, будет находиться в равновесии, если её поместить в некоторую точку А между зарядами q1 и q2 на прямой, соединяющей эти заряды (рис. 102.1). Пусть заряд q3 < 0. Тогда со стороны зарядов q1 и q2 на заряд q3 будут действовать противоположно направленные кулоновские силы притяжения и
. Согласно второму закону Ньютона, эта бусинка будет покоиться, если модули сил F13 и F23 равны. Тогда, приняв расстояние от заряда q1 до точки А равным х, запишем:
. Так как k и q3 не равны нулю, то это выражение можно сократить:
. Извлечём из обеих частей равенства квадратный корень
. Отсюда:
Такое же значение х мы получим, если примем заряд q3 бусинки положительным (проверьте это самостоятельно).
б) Результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю, если, например, третья бусинка притягивает вторую силой, модуль которой равен модулю силы
, какой её отталкивает первая бусинка (рис. 102.2). При этом заряд третьей бусинки должен быть отрицательным, т. е. q3 < 0. Тогда
. Отсюда
.
Ответ: х = 16 см, расстояние до бусинки с зарядом q3 не зависит от значения и знака её заряда; если заряд бусинки q3 = ‒14 нКл, то результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю.
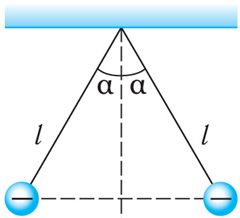
Пример 4. Два одинаковых маленьких проводящих шарика массой m = 20 мг каждый подвешены в воздухе на лёгких нерастяжимых нитях длиной l = 0,20 м, закреплённых в одной точке подвеса. Один из шариков отвели в сторону, сообщили ему заряд q < 0 и отпустили. После столкновения шарики разошлись так, что угол между нитями составил 2α = 60° (рис. 102.3). Определите заряд, который был сообщён первому шарику, а также количество избыточных электронов на каждом из шариков после их столкновения.
m = 20 мг = 2,0·10–5 кг
l = 0,20 м
2α = 60°
N – ?
Решение: Воспользуемся законом сохранения электрического заряда. При столкновении двух одинаковых проводящих шариков сообщённый одному из них заряд разделился поровну и на каждом шарике оказался избыточный отрицательный заряд . На каждый шарик действуют сила тяжести
сила электростатического взаимодействия
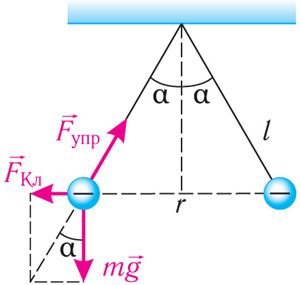
и сила упругости нити
(рис. 102.4). После столкновения шарики разошлись, и установилось равновесие. Векторная сумма сил, действующих на каждый шарик, стала равной нулю:
. Модуль силы электростатического взаимодействия
. Поскольку шарики разошлись симметрично относительно вертикали, проходящей через точку подвеса нитей, то
(рис. 102.4). Следовательно,
. Так как
, то
, откуда
. Примем
.
Количество избыточных электронов на каждом шарике .
Ответ: q = ‒45 нКл, N = 1,4 · 1011.