§ 17. Взаимодействие точечных зарядов. Закон Кулона
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 17. Взаимодействие точечных зарядов. Закон Кулона |
| Напечатано:: | Гость |
| Дата: | Среда, 30 Июль 2025, 20:51 |
Электрически заряженные тела (частицы) взаимодействуют друг с другом. Но как определить силу, которой одно заряженное тело притягивает или отталкивает другое?
Вы уже встречались с физическими моделями при изучении механики (материальная точка) и молекулярной физики (идеальный газ). В электростатике при изучении взаимодействия электрически заряженных тел эффективной оказывается модель «точечный заряд».
Точечный заряд — заряд такого заряженного тела, размеры которого значительно меньше расстояния от этого тела до точки наблюдения и до других тел (т. е. размерами заряженного тела в условиях данной задачи можно пренебречь).
Вспомните, закон всемирного тяготения также сформулирован для точечных тел (материальных точек).
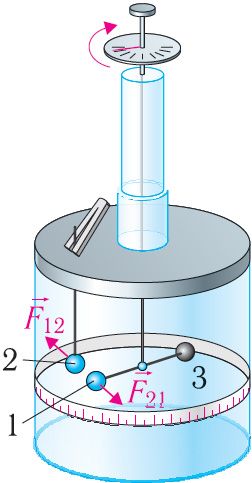
Закон Кулона. Кулон детально исследовал взаимодействие неподвижных точечных зарядов. Он на опыте изучил зависимость сил электрического взаимодействия тел от модулей зарядов этих тел и расстояния между ними.
В своих опытах Кулон использовал специальный прибор — крутильные весы (рис. 98). Крутильные весы представляют собой два стеклянных цилиндра, внутри которых на тонкой серебряной нити подвешено лёгкое непроводящее коромысло. На одном конце коромысла закреплён проводящий шар 1, а на другом — бумажный противовес 3. Шар 1 можно заряжать с помощью такого же проводящего шара 2. Он находится на изолирующем стержне, закреплённом на крышке нижнего цилиндра. При соприкосновении шара 1 с заряженным шаром 2 заряд распределяется между ними поровну, и шары отталкиваются.
![]()
Используя крутильные весы, Кулон получил зависимость модуля сил взаимодействия двух заряженных шаров от величин зарядов и от расстояния между ними. По углу закручивания нити, отсчитываемому по шкале прибора, можно определить силу взаимодействия заряженных шаров. Кулон установил, что модуль сил взаимодействия двух заряженных шаров обратно пропорционален квадрату расстояния между ними:
.
Для измерения зависимости модуля сил взаимодействия шаров от их зарядов учёный нашёл простой способ. Разряжая шар 2 прикосновением руки, а затем касаясь им уже заряженного шара 1, Кулон смог получить на нём заряды, модуль которых в 2, 4, 8 и т. д. раз меньше первоначального. Он выяснил, что при неизменном расстоянии модуль сил взаимодействия двух неподвижных небольших заряженных тел прямо пропорционален произведению модулей электрических зарядов каждого из них: .
Обобщив экспериментальные данные, Кулон сформулировал закон, получивший его имя.
Закон Кулона: модули сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорциональны произведению модулей зарядов этих тел, обратно пропорциональны квадрату расстояния между ними, а сами силы направлены вдоль прямой, соединяющей эти тела:
(17.1)
где k — коэффициент пропорциональности, зависящий от выбора единиц физических величин; |q1| и |q2| — модули точечных зарядов; r — расстояние между ними.
В СИ коэффициент пропорциональности
где — электрическая постоянная.
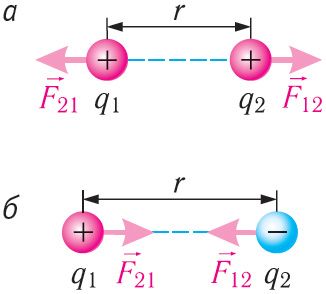
Силы и
взаимодействия неподвижных точечных зарядов (рис. 99) называют кулоновскими силами. В соответствии с третьим законом Ньютона эти силы противоположно направлены
, а их модули равны. Отметим, что силы электростатического взаимодействия являются силами отталкивания для одноимённых зарядов (рис. 99, а) и силами притяжения для разноимённых (рис. 99, б).
Два маленьких положительно заряженных шарика закреплены на расстоянии r друг от друга. Как изменится модуль сил электростатического взаимодействия шариков, если: 1) уменьшить заряд каждого шарика в четыре раза; 2) увеличить расстояние между шариками в четыре раза; 3) увеличить заряд каждого шарика и расстояние между ними в два раза?
Как изменились бы силы электростатического взаимодействия шариков, если бы: 1) шарики были заряжены отрицательно; 2) один из шариков зарядить отрицательно, а другой положительно?
![]()
Интересно знать
Экспериментальные факты свидетельствуют о том, что воздействие неподвижного в данной инерциальной системе отсчёта точечного заряда на движущийся точечный заряд может быть описано законом Кулона с приемлемой точностью. Так, описание рассеяния α-частиц на ядрах атомов золота в опытах Резерфорда с помощью модели точечного заряда, на который действует кулоновская сила со стороны неподвижного ядра, согласуется с экспериментальными данными в пределах точности последних.
Два и более движущихся в данной инерциальной системе заряда не могут характеризоваться только кулоновским взаимодействием, так как каждый из них создаёт в окружающем пространстве магнитное поле, которое действует магнитной силой на остальные заряды, движущиеся в нём.
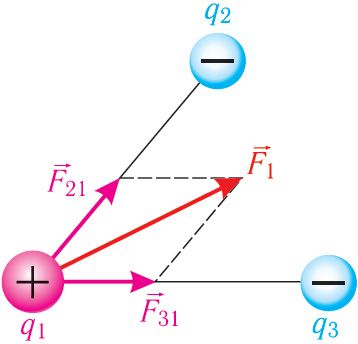
Взаимодействие системы точечных зарядов. Экспериментально установили, что силы взаимодействия двух точечных зарядов не изменяются при появлении третьего точечного заряда или любого числа точечных зарядов. В этом случае силы воздействия ,
, ...,
каждого из зарядов q2, q3, …, qn на заряд q1 определяют по закону Кулона. Результирующая сила является векторной суммой сил, которыми каждый из этих зарядов в отдельности воздействует на заряд q1 (принцип суперпозиции).
Используя принцип суперпозиции и закон Кулона, можно описать электростатическое взаимодействие любой системы точечных зарядов. На рисунке 100 представлены три взаимодействующих между собой точечных электрических заряда: q1 > 0, q2 < 0, q3 < 0. Результирующей сил, действующих на заряд q1 со стороны зарядов q2 и q3, является сила , которая равна векторной сумме сил
и
:
. Силы
и
воздействия зарядов q2 и q3 на заряд q1 определяют по закону Кулона.
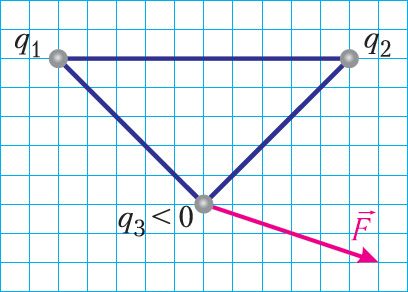
Точечные заряды q1, q2 и q3 закреплены в вершинах треугольника. Направление результирующей электростатической силы, действующей на отрицательный заряд q3 со стороны зарядов q1 и q2, представлено на рисунке 101. Каковы знаки зарядов q1 и q2? Во сколько раз отличаются модули зарядов q1 и q2?
![]()
Интересно знать
Понятие электрического заряда в некоторой степени сходно с понятием гравитационной массы. Электрический заряд определяет интенсивность электромагнитных взаимодействий, а масса — гравитационных. Закон Кулона, описывающий электростатическое взаимодействие, формально похож на закон всемирного тяготения Ньютона, определяющий силы гравитационного взаимодействия:
В обоих случаях модуль сил взаимодействия:
– обратно пропорционален квадрату расстояния между материальными точками;
– прямо пропорционален величинам, характеризующим те свойства тел (материальных точек), которые определяют взаимодействия, — массам в одном случае и электрическим зарядам — в другом.
Для измерения сил электрического отталкивания (Ш. Кулон, 1785 г.) и гравитационной постоянной (Г. Кавендиш, 1788 г.) учёные использовали похожие по устройству экспериментальные установки.
Однако между силами гравитационного и электростатического взаимодействий существует и важное различие. Ньютоновские силы тяготения — это всегда силы притяжения. кулоновские же силы взаимодействия зарядов могут быть как силами притяжения (между разноимёнными зарядами), так и силами отталкивания (между одноимёнными зарядами).
![]()
Известно, что масса электрона mе = 9,1· 10–31 кг. Во сколько раз модуль сил электрического отталкивания между двумя электронами больше модуля сил их гравитационного притяжения?
Диэлектрическая проницаемость вещества. Из опытов следует, что взаимодействие электрически заряженных тел в воздухе практически не отличается от их взаимодействия в вакууме. Если заряженные тела находятся в воде, керосине, масле или какой-нибудь другой непроводящей среде, то модуль сил их взаимодействия оказывается меньше, чем в вакууме. Чтобы учесть влияние среды, ввели её специальную характеристику, называемую диэлектрической проницаемостью.
Диэлектрическая проницаемость вещества — физическая величина, показывающая, во сколько раз модуль сил электростатического взаимодействия зарядов в данной однородной среде меньше модуля сил взаимодействия этих же зарядов в вакууме:
(17.2)
где F0 и F — модули сил электростатического взаимодействия зарядов в вакууме и в однородной среде соответственно.
С учётом соотношения (17.2) закон Кулона можно записать следующим образом:
Диэлектрическая проницаемость вакуума равна 1. За 1 принимают и диэлектрическую проницаемость воздуха, поскольку её значение (при нормальном атмосферном давлении) 1,0006. Диэлектрические проницаемости других однородных сред всегда больше единицы. Например, у воды диэлектрическая проницаемость 81, у глицерина — 56, а у керосина — 2.
Как и во сколько раз отличаются модули сил электростатического взаимодействия двух точечных зарядов, находящихся на одинаковом расстоянии друг от друга в воде, керосине и глицерине?
Интересно знать
Диэлектрическая проницаемость дистиллированной воды при температуре 25 °C равна 78,54, а при температуре 0 °C — 88. Обычно без указания температуры диэлектрическую проницаемость воды полагают равной 81.

1. К какому виду взаимодействий относят взаимодействие неподвижных электрических зарядов (заряженных тел)?
2. Заряды каких заряженных тел можно считать точечными?
3. Опишите эксперименты Кулона по исследованию взаимодействия электрических зарядов.
4. Сформулируйте закон Кулона. Каковы условия применимости закона Кулона?
5. Чему равен в СИ коэффициент k? Выразите наименование коэффициента пропорциональности k в законе Кулона в основных единицах СИ.
6. В чём суть принципа суперпозиции для электрического взаимодействия точечных зарядов?
7. Что называют диэлектрической проницаемостью среды?
![]()
Пример 1. Два точечных заряда находятся в керосине на расстоянии r1 = 42 см. Определите, на каком расстоянии должны находиться эти заряды в глицерине, чтобы модуль сил их электростатического взаимодействия остался прежним. Диэлектрические проницаемости керосина ε1 = 2,0, глицерина ε2 = 56,2.
r1 = 42 см
Fк1 = Fк2
ε1 = 2,0
ε2 = 56,2
Решение: Поскольку Fк1 = Fк2, то, воспользовавшись законом Кулона, можно записать: .
Следовательно, .
Ответ: r2 = 7,9 см.
Пример 2. Точечные заряды q1 = 3,4 нКл и q2 = –5,6 нКл находятся в вакууме на расстоянии r = 36 см. Определите модуль и направление результирующей силы, действующей на заряд q3 = 3,2 нКл, помещённый в точку пространства, находящуюся на середине отрезка, соединяющего эти заряды.
q1 = 3,4 нКл = 3,4 · 10–9 Кл
q2 = –5,6 нКл = –5,6 · 10–9 Кл
r = 36 см = 0,36 м
q3 = 3,2 нКл = 3,2 · 10–9 Кл
Решение: Изобразим на рисунке силы и
, действующие на точечный заряд q3 со стороны точечных зарядов q1 и q2 соответственно. Построив векторную сумму сил
и
, определим, что результирующая
этих сил направлена к заряду q2 (рис. 102).
Поскольку силы и
направлены одинаково, то модуль результирующей силы
.
Таким образом,
Ответ: Fp = 8,0 мкН; сила направлена к заряду q2.
![]()
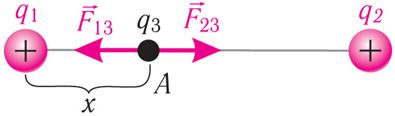
Пример 3. Две бусинки, электрические заряды которых q1 = 40 нКл и q2 = 90 нКл, закреплены на непроводящем стержне на расстоянии r = 40 см друг от друга. Определите: а) где надо поместить третью бусинку, имеющую заряд q3, чтобы она оказалась в равновесии; б) каким должен быть заряд q3 третьей бусинки, чтобы результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равнялась нулю.
q1 = 40 нКл = 4,0·10–8 Кл
q2 = 90 нКл = 9,0·10-8 Кл
r = 40 см = 0,40 м
q3 — ?
Решение: а) Третья бусинка, имеющая заряд q3, будет находиться в равновесии, если её поместить в некоторую точку А между зарядами q1 и q2 на прямой, соединяющей эти заряды (рис. 102.1). Пусть заряд q3 < 0. Тогда со стороны зарядов q1 и q2 на заряд q3 будут действовать противоположно направленные кулоновские силы притяжения и
. Согласно второму закону Ньютона, эта бусинка будет покоиться, если модули сил F13 и F23 равны. Тогда, приняв расстояние от заряда q1 до точки А равным х, запишем:
. Так как k и q3 не равны нулю, то это выражение можно сократить:
. Извлечём из обеих частей равенства квадратный корень
. Отсюда:
Такое же значение х мы получим, если примем заряд q3 бусинки положительным (проверьте это самостоятельно).
б) Результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю, если, например, третья бусинка притягивает вторую силой, модуль которой равен модулю силы
, какой её отталкивает первая бусинка (рис. 102.2). При этом заряд третьей бусинки должен быть отрицательным, т. е. q3 < 0. Тогда
. Отсюда
.
Ответ: х = 16 см, расстояние до бусинки с зарядом q3 не зависит от значения и знака её заряда; если заряд бусинки q3 = ‒14 нКл, то результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю.
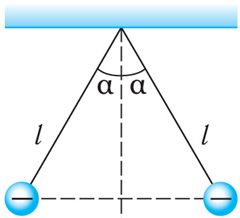
Пример 4. Два одинаковых маленьких проводящих шарика массой m = 20 мг каждый подвешены в воздухе на лёгких нерастяжимых нитях длиной l = 0,20 м, закреплённых в одной точке подвеса. Один из шариков отвели в сторону, сообщили ему заряд q < 0 и отпустили. После столкновения шарики разошлись так, что угол между нитями составил 2α = 60° (рис. 102.3). Определите заряд, который был сообщён первому шарику, а также количество избыточных электронов на каждом из шариков после их столкновения.
m = 20 мг = 2,0·10–5 кг
l = 0,20 м
2α = 60°
N – ?
Решение: Воспользуемся законом сохранения электрического заряда. При столкновении двух одинаковых проводящих шариков сообщённый одному из них заряд разделился поровну и на каждом шарике оказался избыточный отрицательный заряд . На каждый шарик действуют сила тяжести
сила электростатического взаимодействия
и сила упругости нити
(рис. 102.4). После столкновения шарики разошлись, и установилось равновесие. Векторная сумма сил, действующих на каждый шарик, стала равной нулю:
. Модуль силы электростатического взаимодействия
. Поскольку шарики разошлись симметрично относительно вертикали, проходящей через точку подвеса нитей, то
(рис. 102.4). Следовательно,
. Так как
, то
, откуда
. Примем
.
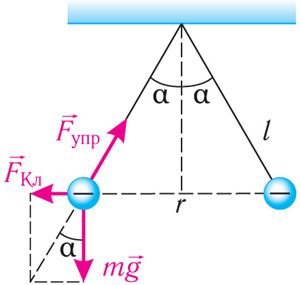
Количество избыточных электронов на каждом шарике .
Ответ: q = ‒45 нКл, N = 1,4 · 1011.
Упражнение 13
1. Определите модуль сил взаимодействия двух одинаковых неподвижных точечных зарядов q1 = q2 = 9,0 нКл, находящихся на расстоянии r = 0,30 м в вакууме. Во сколько раз уменьшится или увеличится модуль сил взаимодействия этих зарядов при помещении их в керосин, диэлектрическая проницаемость которого ε = 2,0?
2. Определите, во сколько раз следует увеличить расстояние между двумя неподвижными точечными зарядами, чтобы модуль сил взаимодействия остался прежним при увеличении численного значения одного из зарядов в α = 4 раза.
3. Два одинаковых маленьких проводящих шарика, заряды которых отличаются в два раза, находятся на расстоянии r = 50 см. Определите расстояние, на которое необходимо развести шарики после соприкосновения, чтобы модуль сил их взаимодействия остался прежним.
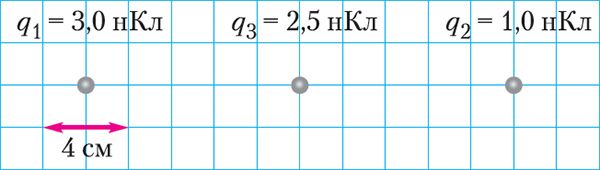
4. Точечные заряды q1 и q2 закреплены в вакууме (рис. 103). Определите модуль и направление результирующей силы, действующей на заряд q3, помещённый в точку, находящуюся на середине отрезка, соединяющего эти заряды.
5. Заряды двух одинаковых маленьких шариков массой m = 40 г каждый одинаковые. Расстояние между шариками существенно превышает их размеры. Определите модуль зарядов шариков, если кулоновская сила их отталкивания уравновешивает силу гравитационного притяжения этих шариков.
6. Небольшой шарик, заряд которого q1 = 20 нКл и масса m = 60 мг, подвешен в воздухе на шёлковой нити. После того как на вертикали, проходящей через центр шарика, на расстоянии r = 15 см ниже его поместили другой маленький шарик, заряженный отрицательно, модуль силы упругости нити увеличился в два раза. Определите заряд второго шарика.
![]()
7. Три первоначально закреплённых одинаковых точечных заряда q1 = q2 = q3 = q0 = 1,0 мкКл расположены в вершинах равностороннего треугольника. Определите, какой точечный заряд нужно поместить в центр треугольника, чтобы вся система находилась в равновесии после освобождения первоначально закреплённых зарядов.