§ 12. Работа в термодинамике

Примеры решения задач
Рис.
Рис. 73

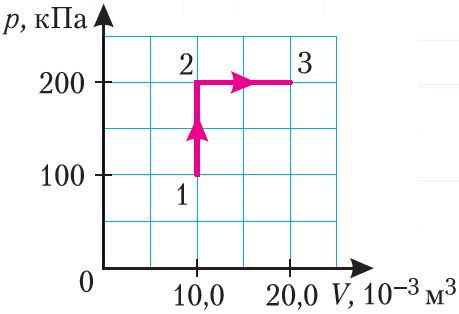
Пример 1. Определите работу, совершаемую силой давления идеального газа определённой массы при переходе из состояния 1 в состояние 3 (рис. 73).

Решение. I способ. Работа А газа в ходе всего процесса равна сумме работ на участках 1rightwards arrow2 и 2rightwards arrow3. Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс V2 = V1), то работа, совершаемая силой давления газа, А12 = 0. В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу

A23 = p2ΔV = p2(V3 – V1).

Тогда при переходе из состояния 1 в состояние 3 работа

А = А12 + А23 = p2(V3–V1).

А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.

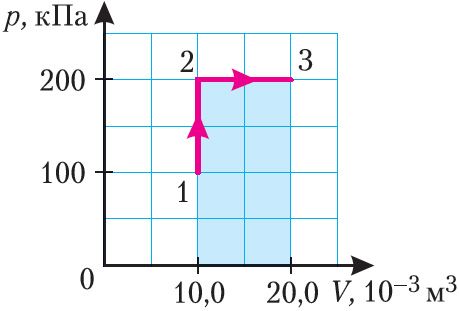
Рис. 74
Рис. 74

II способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью ОV и прямыми, соответствующими значениям объёма V1 = 10,0 · 10–3 м3 и V2 = 20,0 · 10–3 м3 (закрашенная область на рисунке 74).

А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.

Ответ: А = 2,00 кДж.

Пример 2. Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от t1 = 12 °С до t2 = 87 °С, если давление газа p = 190 кПа, а его начальный объём V1 = 6,0 дм3.

Дано:
Т1 = 285 К
Т2 = 360 К
p = 190 кПа = 1,90 · 105 Па
V1 = 6,0 дм3 = 6,0 · 10–3 м3
А — ?

Решение: Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому

A space equals space p left parenthesis V subscript 2 space – space V subscript 1 right parenthesis space equals space p V subscript 2 space – space p V subscript 1.

Согласно уравнению Клапейрона–Менделеева, p V subscript 1 space equals space nu R T subscript 1 и p V subscript 2 space equals space nu R T subscript 2. Следовательно,

A space equals space v R left parenthesis T subscript 2 space minus space T subscript 1 right parenthesis space equals space v R T subscript 1 open parentheses T subscript 2 over T subscript 1 minus 1 close parentheses space equals space p V subscript 1 open parentheses T subscript 2 over T subscript 1 minus 1 close parentheses.

A space equals space 1 comma 90 times 10 to the power of 5 space Па space times 6 comma 0 times 10 to the power of negative 3 end exponent space space straight м cubed times open parentheses fraction numerator 360 space straight К over denominator 285 space straight К end fraction minus 1 close parentheses space equals space 3 comma 0 times 10 squared space Дж space equals space 0 comma 30 space кДж.

Ответ: A space equals space 0 comma 30 space кДж.

Рис.
Рис. 74.1

Материал повышенного уровня

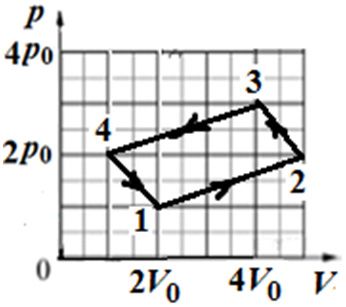
Пример 3. На рисунке 74.1 изображен процесс изменения состояния идеального газа определённой массы. На каком участке сила давления газа совершила наименьшую положительную работу? На каком участке внешняя сила совершила наибольшую положительную работу?

Решение. Работе силы давления газа соответствует площадь под графиком процесса. При расширении газа сила давления совершает положительную работу, а внешняя сила — отрицательную. При сжатии газа наоборот: сила давления совершает отрицательную работу, а внешняя сила — положительную. Анализ графика позволяет сделать вывод, что в процессе перехода из состояния 4 в состояние 1 сила давления газа совершила минимальную положительную работу (газ расширялся, а площадь под графиком минимальна). Максимальную же положительную работу внешняя сила совершает при сжатии, когда площадь под графиком максимальна (это процесс перехода из состояния 3 в состояние 4).

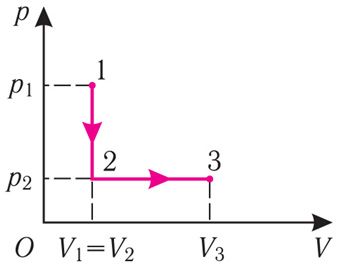
Пример 4. Состояние идеального газа, взятого в количестве ν = 1,0 моль при абсолютной температуре Т1 = 300 К, изменяется так, как изображено на рисунке 74.2. Определите работу газа в ходе всего процесса, если на изохоре 1rightwards arrow2 его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.

Дано:
ν = 1,0 моль
Т1 = 300 К
p1 = 3p2
Т1 = Т3
A – ?

Решение: Работа А газа в ходе всего процесса равна сумме значений работы на участках 1rightwards arrow2 и 2rightwards arrow3 (рис. 74.2). Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный V2 = V1), то работа газа А12 = 0. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (р2 = р3), следовательно, работа газа А23 = p2(V3 − V1). Тогда А = А12 + А23 = p2(V3 − V1). Так как по условию Т1 = Т3, то воспользуемся уравнением Клапейрона: fraction numerator p subscript 1 V subscript 1 over denominator T subscript 1 end fraction equals fraction numerator p subscript 2 V subscript 3 over denominator T subscript 3 end fraction, откуда V subscript 3 equals p subscript 1 over p subscript 2 V subscript 1 equals 3 V subscript 1. Следовательно, A equals p subscript 2 open parentheses 3 V subscript 1 minus V subscript 1 close parentheses equals 2 p subscript 2 V subscript 1 equals fraction numerator 2 p subscript 1 V subscript 1 over denominator 3 end fraction.

Рис.
Рис. 74.2

Согласно уравнению Клапейрона‒Менделеева, p1V1 = νRT1. Тогда A equals 2 over 3 nu R T subscript 1.

A equals fraction numerator 2 times 1 comma 0 space моль times 8 comma 31 space begin display style fraction numerator Дж over denominator straight К times моль end fraction end style times 300 space straight К over denominator 3 end fraction equals 1662 space Дж equals 1 comma 7 space кДж.

Ответ: А = 1,7 кДж.