§ 12. Работа в термодинамике
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 12. Работа в термодинамике |
| Напечатано:: | Гость |
| Дата: | Пятница, 4 Апрель 2025, 01:30 |
В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.
Работа в термодинамике. Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.
Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.
Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.
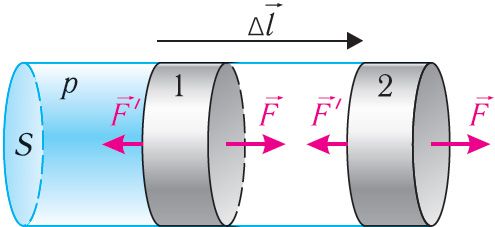
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре р. В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние Δl. Модуль силы давления газа на поршень F = pS. Эта сила совершила работу по перемещению поршня, равную
,
где — угол между направлениями силы
и перемещения поршня
.
Поскольку в рассматриваемом примере α = 0 и cosα = 1, то
.
Произведение SΔl определяет изменение объёма ∆V = V2 – V1, где V1 — начальный объём газа; V2 — объём газа в конечном состоянии (см. рис. 66).
Таким образом, работа силы давления газа при его изобарном расширении:
.
(12.1)
Так как давление р газа — величина положительная, то из формулы (12.1) следует, что A12 > 0.
При изобарном расширении газа из состояния 1 в состояние 2 работа силы (см. рис. 66):
,
где — модуль силы, действующей на газ со стороны поршня (внешняя сила);
— угол между направлениями силы
и перемещения
поршня.
Перемещение поршня одно и то же, а сила давления
газа на поршень и сила давления
поршня на газ — силы, подчиняющиеся третьему закону Ньютона:
.
Следовательно, работы и
отличаются только знаком (
):
.
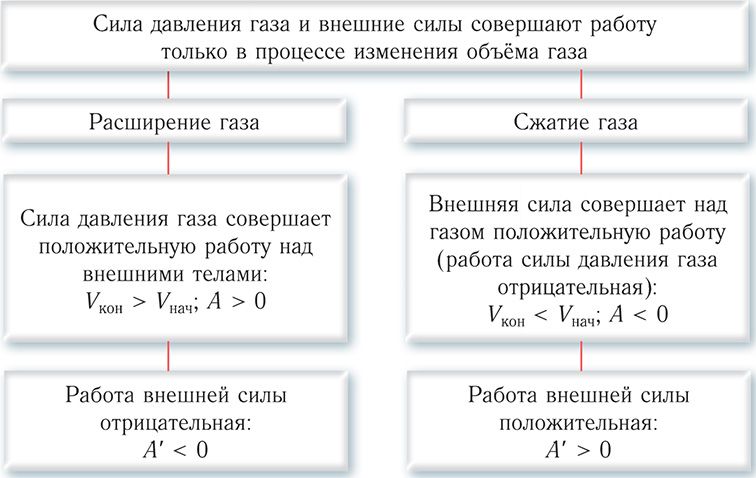
Таким образом, можно сделать следующие выводы.
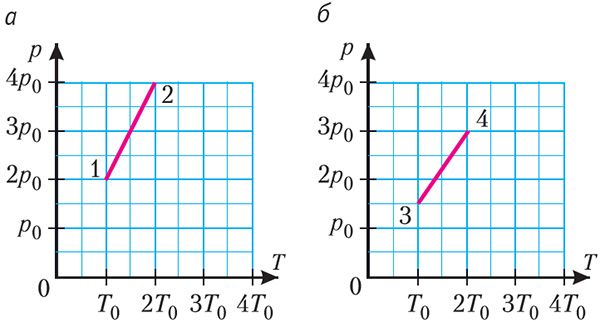
На рисунке 67, а представлен процесс перехода идеального газа определённой массы из состояния 1 в состояние 2, а на рисунке 67, б — процесс перехода этого же газа из состояния 3 в состояние 4. Сравните работы, совершённые силой давления газа в обоих процессах, и изменения значений его внутренней энергии.
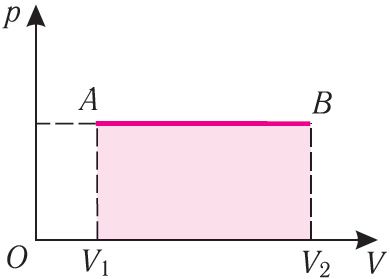
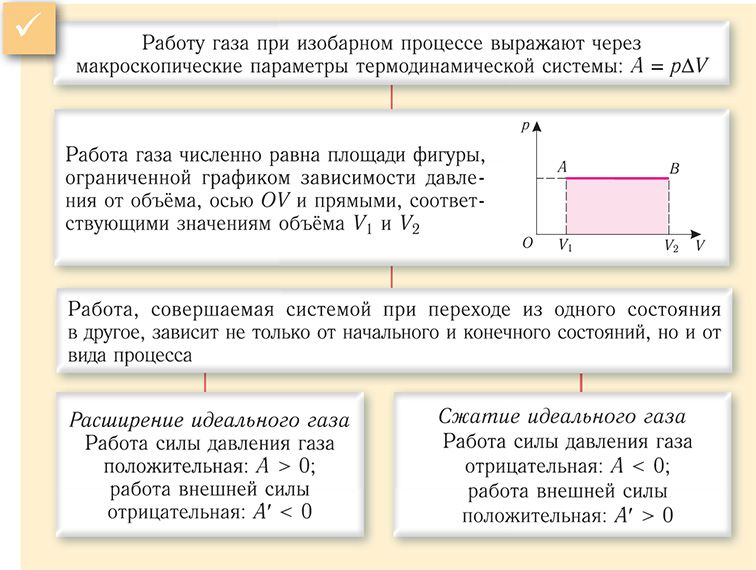
Геометрическое толкование работы. Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при р = const (рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника V1АВV2.
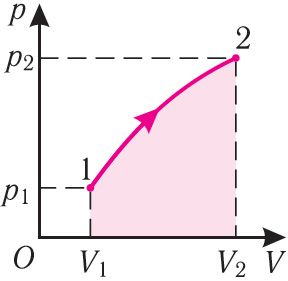
Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от V1 до V2 численно равна площади фигуры, ограниченной графиком процесса (кривая 12), осью ОV и прямыми, соответствующими значениям объёмов V1 и V2.
![]()
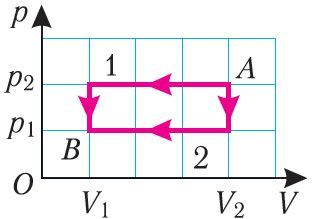
Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 69.1). Работа, совершаемая системой при циклическом процессе, или работа цикла, численно равна площади фигуры, ограниченной линиями, которые изображают цикл в координатах р, V:
A = A12 + A23 + A31 = S12 + S23 + S31 = S12 + S31 = S1231,
где S23 = 0, S1231 > 0 на рисунке 69.1, а и S1231 < 0 на рисунке 69.1, б.
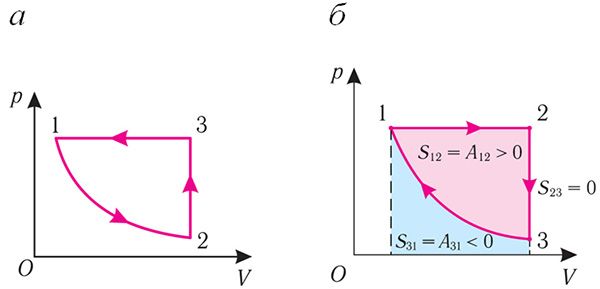
Если «кривая расширения» (изобара 1 2) (рис. 69.1, а) расположена выше «кривой сжатия» (изотерма 3
1), то полная работа, совершённая системой за цикл (работа цикла), положительна. Если же, как изображено на рисунке 69.1, б, «кривая сжатия» (изобара 3
1) расположена выше «кривой расширения» (изотерма 1
2), то работа цикла отрицательна.
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения р2, а затем изобарно увеличив его объём до значения V3. В первом случае работа газа больше, чем во втором.
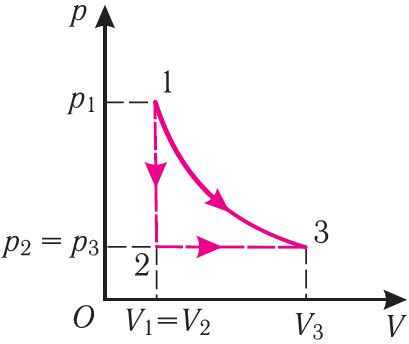
Следовательно, работа, совершаемая термодинамической системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
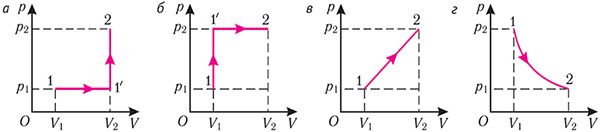
На каком из представленных на рисунках 71, а–г графиков сила давления газа совершает в процессе перехода из состояния 1 в состояние 2:
а) наибольшую работу; б) наименьшую работу?
1. Как вычислить работу, совершаемую силой давления газа при его расширении (сжатии)?
2. Как соотносятся между собой работа силы давления газа и работа внешних сил над газом?
3. В чём заключается геометрический смысл понятия «работа» в термодинамике?
4. Почему расширение газа при отсутствии теплообмена с окружающей средой сопровождается его охлаждением?
5. Идеальный газ переводят из состояния А в состояние В двумя способами: первый раз — А1В, а второй — А2В (рис. 72). В каком случае работа, совершённая силой давления газа, больше? В каком случае изменение внутренней энергии больше?
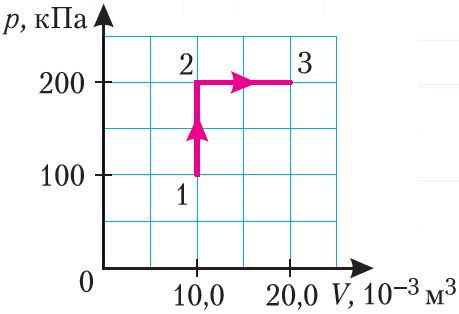
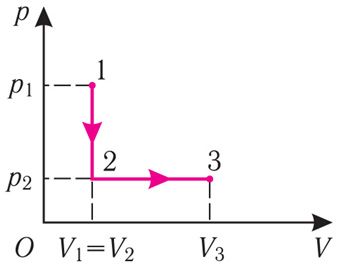
Пример 1. Определите работу, совершаемую силой давления идеального газа определённой массы при переходе из состояния 1 в состояние 3 (рис. 73).
Решение. I способ. Работа А газа в ходе всего процесса равна сумме работ на участках 12 и 2
3. Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс V2 = V1), то работа, совершаемая силой давления газа, А12 = 0. В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу
A23 = p2ΔV = p2(V3 – V1).
Тогда при переходе из состояния 1 в состояние 3 работа
А = А12 + А23 = p2(V3–V1).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
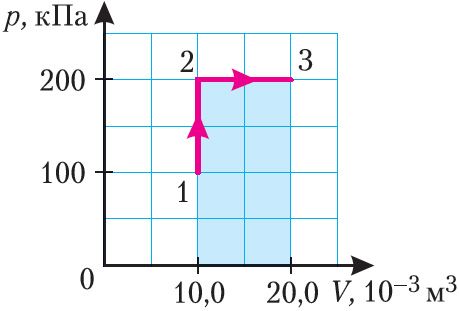
II способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью ОV и прямыми, соответствующими значениям объёма V1 = 10,0 · 10–3 м3 и V2 = 20,0 · 10–3 м3 (закрашенная область на рисунке 74).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
Ответ: А = 2,00 кДж.
Пример 2. Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от t1 = 12 °С до t2 = 87 °С, если давление газа p = 190 кПа, а его начальный объём V1 = 6,0 дм3.
Т1 = 285 К
Т2 = 360 К
p = 190 кПа = 1,90 · 105 Па
V1 = 6,0 дм3 = 6,0 · 10–3 м3
Решение: Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
.
Согласно уравнению Клапейрона–Менделеева, и
. Следовательно,
.
.
Ответ: .
![]()
Пример 3. На рисунке 74.1 изображен процесс изменения состояния идеального газа определённой массы. На каком участке сила давления газа совершила наименьшую положительную работу? На каком участке внешняя сила совершила наибольшую положительную работу?
Решение. Работе силы давления газа соответствует площадь под графиком процесса. При расширении газа сила давления совершает положительную работу, а внешняя сила — отрицательную. При сжатии газа наоборот: сила давления совершает отрицательную работу, а внешняя сила — положительную. Анализ графика позволяет сделать вывод, что в процессе перехода из состояния 4 в состояние 1 сила давления газа совершила минимальную положительную работу (газ расширялся, а площадь под графиком минимальна). Максимальную же положительную работу внешняя сила совершает при сжатии, когда площадь под графиком максимальна (это процесс перехода из состояния 3 в состояние 4).
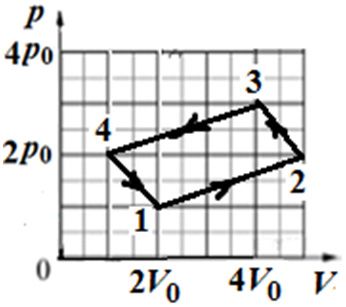
Пример 4. Состояние идеального газа, взятого в количестве ν = 1,0 моль при абсолютной температуре Т1 = 300 К, изменяется так, как изображено на рисунке 74.2. Определите работу газа в ходе всего процесса, если на изохоре 12 его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.
ν = 1,0 моль
Т1 = 300 К
p1 = 3p2
Т1 = Т3
Решение: Работа А газа в ходе всего процесса равна сумме значений работы на участках 12 и 2
3 (рис. 74.2). Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный V2 = V1), то работа газа А12 = 0. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (р2 = р3), следовательно, работа газа А23 = p2(V3 − V1). Тогда А = А12 + А23 = p2(V3 − V1). Так как по условию Т1 = Т3, то воспользуемся уравнением Клапейрона:
, откуда
. Следовательно,
.
Согласно уравнению Клапейрона‒Менделеева, p1V1 = νRT1. Тогда .
Ответ: А = 1,7 кДж.
Упражнение 8
1. Сила давления идеального одноатомного газа определённой массы совершает отрицательную работу в изотермическом процессе. Как изменяются в этом процессе объём, давление и внутренняя энергия газа?
2. Газ, давление которого p = 0,10 МПа, изобарно расширяется. При этом сила давления газа совершает работу А = 40 Дж. Определите, на сколько увеличился объём газа.
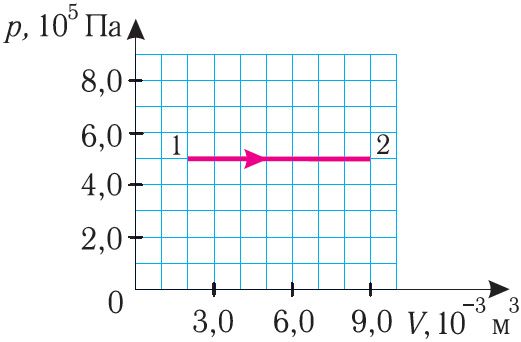
3. На рисунке 75 представлен график зависимости давления газа от объёма. Определите работу, совершённую силой давления газа при расширении.
4. При изобарном увеличении температуры азота на ΔT = 180 К силой его давления совершена работа А = 25 кДж. Определите массу азота.
5. Идеальный газ определённой массы, температура которого T1 = 290 К и давление p = 0,20 МПа, занимает объём V1 = 0,10 м3. Определите работу, совершённую силой давления газа при его изобарном нагревании до температуры T2 = 370 К.
![]()
6. При расширении идеального газа, количество вещества которого ν = 3 моль, его объём увеличился от V1 = 2 дм3 до V2 = 6 дм3. Абсолютная температура газа изменялась по закону T = αV2, где — коэффициент пропорциональности. Определите работу, совершённую силой давления газа при его расширении.