§ 5. Уравнение состояния идеального газа
Упражнение 4
1. Определите количество вещества идеального газа, находящегося в сосуде вместимостью V = 480 см3 при нормальных условиях (атмосферное давление р0 = 1,0 · 105 Па, температура t0 = 0,0 °С).
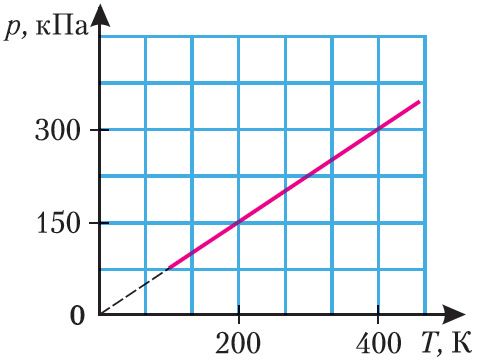
2. На рисунке 20 представлен график зависимости давления водорода, масса которого m = 100 г, от абсолютной температуры. Определите объём, занимаемый газом.
3. Баллон вместимостью V1 = 15 л, содержащий газ, давление которого p1 = 2,0 · 106 Па, соединили с пустым баллоном вместимостью V2 = 5,0 л. Определите давление газа, которое установилось в баллонах, если температура после расширения газа через некоторый промежуток времени оказалась такой же, как и до расширения.
4. Азот, объём которого V1 = 2,9 м3, температура T1 = 293 К и давление p1 = 2,0 · 105 Па, перевели в жидкое состояние. Определите объём, занимаемый жидким азотом, если его плотность .
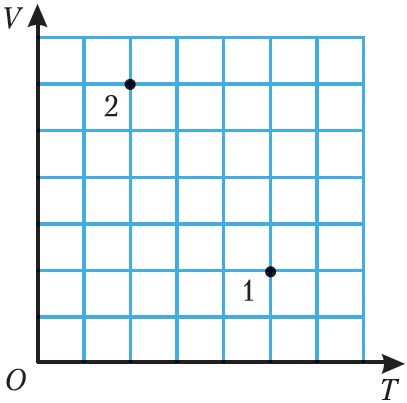
5. На рисунке 21 точки 1 и 2 соответствуют различным состояниям идеального газа определённой массы. Определите, во сколько раз отличаются давления газа в состояниях 1 и 2.
![]()
6. В сосуде вместимостью V = 2,0 л находятся кислород массой m1 = 4,0 г и азот массой m2 = 7,0 г. Определите давление смеси газов, если её абсолютная температура Т = 300 К.
7. В баллоне вместимостью V = 12 л находился идеальный газ, первоначальные давление и температура которого p1 = 1,2 · 105 Па и t1 = 27 °С соответственно. После того как из баллона выпустили часть газа, в нём установилась температура t2 = 17 °С. Определите давление газа, оставшегося в баллоне, если количество вещества выпущенного газа ν1 − ν2 = 0,10 моль.
8. Вакуумированный цилиндрический сосуд вместимостью V = 2 л разделён на две равные части тонкой перегородкой, которая пропускает только молекулы водорода. В одну из частей сосуда впустили водород Н2 и азот N2, массы которых m1 = 4 г и m2 = 14 г соответственно. Определите давление смеси газов, если при достижении теплового равновесия абсолютная температура системы составила Т = 320 К.